第四部:無機化学の基礎 無機化学とは(基本)
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,無機化合物の電気的特性計測に関連し, 【電気伝導率と誘電率】, 【電気特性の測定原理】, 【インピーダンス測定の実施】 に項目を分けて紹介する。
電気伝導率と誘電率
物質に外部から電場を加えた時,物質に流れる電流(有効電流)は,強さや方向が時間によって変わらない定常電流( stationary current,steady current ),電束の時間的変化に伴って流れることを想定した変位電流( displacement current )に分けられる。
定常電流は,定常状態における電気伝導率σの物質に流れる電流密度( j =σE )で表され,
変位電流は,時間と共に変化する電束密度( δD /δt )で表される。
電束密度 D ( electric flux density )は,電磁気学のマクスウェル方程式の一つで,ガウスの法則で定義され,物体の誘電率ε(イプシロン)と電場 E により,
D = εE
で表される。
従って,両者を合わせた有効電流密度 j* は,
J* = j +δD /δt = σE + εδE /δt
で表される。
ここで,電場が周期的に変動する場合を考える。電場の変動周波数を f とすると,角周期 ω = 2πf で与えられるので,有効電流密度は次の複素数で与えられる。
J* = σE + i ωεE
ここで,i は虚数単位を示す。
すなわち,有効電流密度は,電場と位相の等しい実数部分の定常電流と電場と位相がπ/2 ずれた虚数部の変位電流のベクトル和であることを示す。
定常電流の絶対値と変位電流の絶対値の比は,σ/ωεで与えられることになる。すなわち,例えば金属の様に電気伝導率σが大きく,誘電率εが小さい良導体では,σ/ωε≫ 1 となり,定常電流のみを考えて変位電流を無視できる。一方,例えば絶縁体などの物質では,σ/ωε≪ 1 となり,定常電流の寄与が変位電流に比較して小さいことが分かる。
【参考】
電束密度( electric flux density )
電場に誘電率を掛けたベクトル量で,電場の代わりにこれを用いるとガウスの法則が簡単に表現される。電気変位( electric displacement )ともいう。(広辞苑)
ガウスの法則( Gauss' law )
ドイツの物理学者(数学者)カール・フリードリヒ・ガウスが1835年に発見した電荷と電場の関係をあらわす方程式( 1867 年発表)で,イギリスの物理学者ジェームズ・クラーク・マクスウェルが 1864 年に公表した電磁場のモデルであるマクスウェル方程式( Maxwell's equations )の1つである。
誘電率( permittivity )
電束密度が電場の何倍かを示す物理定数で,比誘電率に真空の誘電率ε0 を掛けたもの。
ε0 = 8.854×10-12 C2 N-1 m-2 は基礎定数の一つ。(広辞苑)
ページの先頭へ
電気特性の測定原理
物質の電気伝導率σや誘電率εを,実験的に電位差と電流密度から求めようとした場合に,上述したように,金属などの良導体を除き,多くの物質では変位電流の影響を強く受ける。
定常電流と変位電流の関係は,物質の電気的特性を単純化し,下図のような抵抗( R )とコンデンサー( C )で構成された等価回路を考えるとわかりやすい。
物質に周波数 f の交流を与えると,その電気回路には,周期的な電圧の変動とそれに伴う電流の変動が観察される。物質にある程度の容量成分がある(誘電率が大きい)と,電圧の変動に比較して電流の変動が遅れて現れる。この遅れを位相差θといい,与えた交流の周波数に依存する。
直流電流のオームの法則の電気抵抗 R ( = V /I )の概念を複素数に拡大して考えることができる。この時電気抵抗に相当する値は,交流電圧の最大値( Vmax )と交流電流の最大値( Imax )の比(複素数)に相当し,これを等価回路におけるインピーダンス( impedance )といい,記号 Z (単位Ω)で表す。
図の回路に,周波数 f の交流を与え,電圧( Vmax ),電流( Imax )が得られた時のインピーダンス Z は,物質の抵抗成分(レジスタンス) Rp ,容量成分(キャパシタンタンス) C ,物質以外の導線や接点などの抵抗成分 Rs とすると,
Z = Vmax /Imax = Rs + Rp – i (ω C )-1
位相差 θ = tan-1 (ω C Rp )
で与えられる。
この関係を用い,周波数を変えてインピーダンスを計測することで,物質のRs ,Rp ,及び C を求めることができる。
この計測で得られた抵抗値と静電容量から,次の関係を用いて物質の電気伝導率と誘電率が求められる。
物体の表面積 A ,電極間の距離 d とすると,電気抵抗 Rp は,物体の電気伝導率σと
Rp = σ-1( d /A )
の関係,物体の静電容量 C は,物体の誘電率εと
C = ε( A /d )
の関係を用いて,実験的に求めることが可能である。
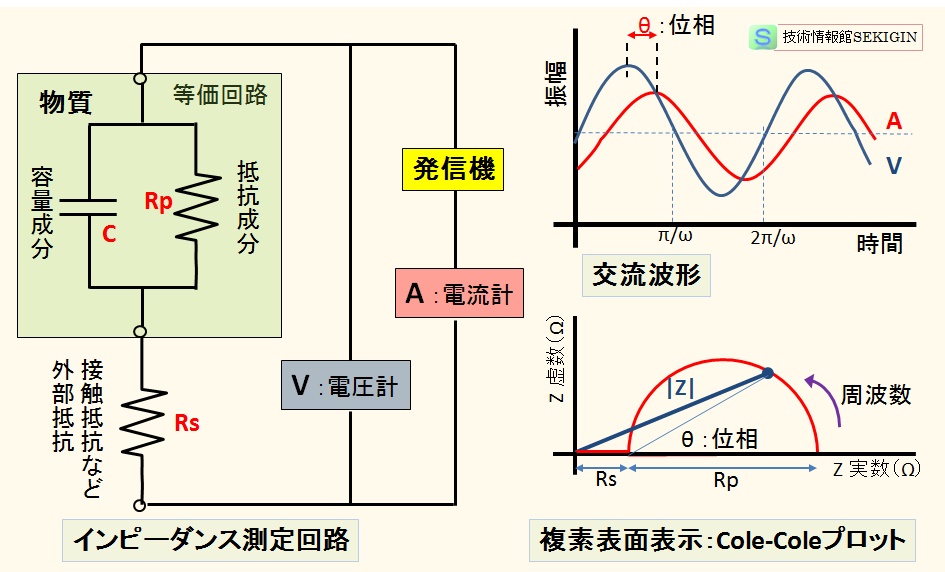
物質のインピーダンス測定原理
【参考】
インピーダンス(impedance)
交流回路中に抵抗,インダクタ,キャパシタが混在する場合の電流の流れ難さを表す量で,位相(phase)を考慮したものである。
正弦波交流の場合の電流と電圧の位相は,抵抗( R )では電流と電圧波形が同位相であるが,インダクタでは電圧波形に対し,電流波形はπ/ 2(rad)遅れ,キャパシタでは,π/ 2(rad)進む。
インダクタ(inductor)
俗にいうコイルで,コイル内の磁場の変化に比例してファラデーの電磁誘導の法則に従い誘導起電力(自己誘導;self-induction)が生じる。
また,誘導電流は,レンツの法則に従い磁場の変化を妨げる方向に流れるので,インダクタは交流電流を遅延させ再形成する能力があり,コンデンサなどを組み合わせることで,特定の周波数の信号だけを取り出す共振回路やフィルタ回路に用いられる。
インダクタには,高周波回路用,一般回路用,デカップリング回路用,電源回路用など多種多様の製品があり,構造,形状,用途などで分類が多数ある。
キャパシタ(capacitor)
コンデンサ,蓄電器ともいわれ,静電容量により電荷を蓄えたり放出したりするための受動素子として用いられる。 コンデンサは,近接し相対する二つの電極(導体)の間に誘電体を挟み電気的に絶縁したものである。誘電体としては,空気,油,雲母,紙,プラスチックフィルム,磁器,酸化被膜等が用いられる。
用いる誘電体により,紙コンデンサ,オイルコンデンサ,真空コンデンサ,ガス封入コンデンサ,プラスチックフィルムコンデンサ,セラミックコンデンサ,電解コンデンサなどがある。他に電気二重層を利用した電気二重層コンデンサ,静電容量を加減できる可変コンデンサなどがある。
位相(phase)
時間とともに周期的に変化する現象において,周期中の位置を示す量をいう。通常は角度(度やラジアン)で表される。
例えば,正弦波で表される周期的な時間変化を y(t) = A sin(ωt + α) で表したとき,(ωt + α) を位相と言う。 なお,t = 0 の位相( α )は特に初期位相と呼ばれる。
交流(電圧・電流)の実効値
交流電圧・電流は時々刻々で変化するので,家庭で用いているような正弦波の交流では,直流における電流・電圧に換算したときに相当する値として,最大値の 2-1/2(≒ 0.707 )倍の値(実効値という)を用いるのが一般的である。
ページの先頭へ
インピーダンス測定の実施
実際の物質では,図に示す簡単な等価回路で解析できない場合も少なくない。実際には,周波数を変えてインピーダンスを測定し,その結果を複素表面表示( cole – cole プロット)することで,該当する等価回路(抵抗とコンデンサ)を推定できる。この場合に,電磁気学で扱うコイル成分(インダクタンス)は,多くの場合に考慮する必要が無い。
想定した等価回路から,構成因子の抵抗成分,容量成分を解析することで,物質の電気伝導率と誘電率が求まる。
等価回路と複素表面表示の関係の例を下図に示す。
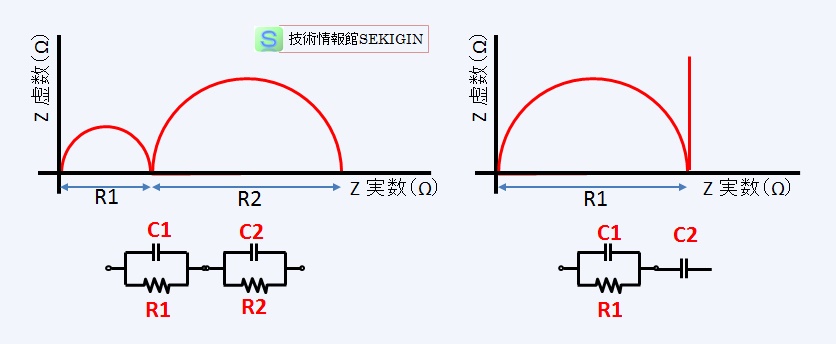
等価回路とインピーダンスの複素表面表示例
ページの先頭へ