物理 第六部:電磁気学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,代表的な交流回路の合成インピーダンスの求め方について, 【インピーダンスとは】, 【素子 1 個のインピーダンス】, 【素子 2 個の合成インピーダンス】, 【 RLC 直列回路】, 【 RLC 並列回路】 に項目を分けて紹介する。
【インピーダンスとは】
インピーダンス(impedance)とは,交流回路中に抵抗,インダクタ,キャパシタが混在する場合の電流の流れ難さを表す量で,位相(phase)を考慮したものである。
正弦波交流の場合の電流と電圧の位相は,抵抗( R )では電流と電圧波形が同位相であるが,インダクタでは電圧波形に対し,電流波形はπ/ 2(rad)遅れ,キャパシタでは,π/ 2(rad)進む。
インピーダンスは,直流回路の電気抵抗(レジスタンス)に相当し,記号 Z ,単位Ωを用いるが,一般には複素数で表示するフェーザ表示(phasor)を用いて表される。
複素数のインピーダンスにおいて,実数部をレジスタンスや抵抗成分,虚数部をリアクタンスという。
なお,インピーダンスの逆数はアドミッタンス(admittance)といい,直流回路の電気伝導度(コンダクタンス)に相当し,記号 S ,単位ジーメンスを用いる。
なお,フェーザ表示とは,電気工学や波動光学などにおいて正弦信号を複素数で表現する表示方法である。
抵抗(XR ),容量性リアクタンス(XC ),誘導性リアクタンス(XL )は,虚数単位 j ,角周波数ω( rad/ s ),抵抗( R ),静電容量( C ),自己インダクタンス( L )を用いたフェーザ表示では,
![]()
で与えられ,交流回路では,後述するように,これらの組み合わせによる合成インピーダンス(combined impedance)となる。
例えば RLC 直列回路の合成インピーダンス Z の大きさは,
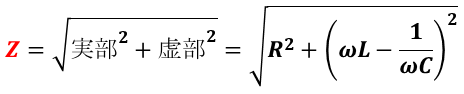
で与えられる。
【参考:基礎用語】
- コンデンサ(capacitor)
キャパシタ,蓄電器ともいわれ,静電容量により電荷を蓄えたり放出したりするための受動素子として用いられる。 コンデンサは,近接し相対する二つの電極(導体)の間に誘電体を挟み電気的に絶縁したものである。誘電体としては,空気,油,雲母,紙,プラスチックフィルム,磁器,酸化被膜等が用いられる。
用いる誘電体により,紙コンデンサ,オイルコンデンサ,真空コンデンサ,ガス封入コンデンサ,プラスチックフィルムコンデンサ,セラミックコンデンサ,電解コンデンサなどがある。他に電気二重層を利用した電気二重層コンデンサ,静電容量を加減できる可変コンデンサなどがある。 - インダクタ(inductor)
俗にいうコイルで,コイル内の磁場の変化に比例してファラデーの電磁誘導の法則に従い誘導起電力(自己誘導;self-induction)が生じる。
また,誘導電流は,レンツの法則に従い磁場の変化を妨げる方向に流れるので,インダクタは交流電流を遅延させ再形成する能力があり,コンデンサなどを組み合わせることで,特定の周波数の信号だけを取り出す共振回路やフィルタ回路に用いられる。
インダクタには,高周波回路用,一般回路用,デカップリング回路用,電源回路用など多種多様の製品があり,構造,形状,用途などで分類が多数ある。 - 位相(phase)
時間とともに周期的に変化する現象において,周期中の位置を示す量をいう。通常は角度(度やラジアン)で表される。
例えば,正弦波で表される周期的な時間変化を y(t) = A sin(ωt + α) で表したとき,(ωt + α) を位相と言う。 なお,t = 0 の位相( α )は特に初期位相と呼ばれる。 - リアクタンス(reactance)
直流回路の電気抵抗(レジスタンス)に相当する交流回路のインピーダンスを複素数で表示した時の虚数部をいう。なお,実数部はレジスタンスや抵抗成分という。
リアクタンスには,インダクタンス(コイル)による誘導性リアクタンスとコンデンサによる容量性リアクタンスがある。 - 合成静電容量(combined capacity)
並列接続では,各静電容量 Ci に対し,それぞれ等しい全電圧 V がかかるため,合成静電容量 C は各静電容量 Ci の総和に等しい。
直列接続では,各静電容量 Ci にかかる電圧 Vi の総計が加えた電圧 V になるので,合成静電容量 C は各静電容量 Ci の逆数の総和の逆数に等しくなる。 - 相互誘導(mutual induction)
二つのコイル( A , B )が磁気的に結合しているとき,2つのコイルに流れる電流が互いに影響を及ぼす現象をいう。例えば,回路 A を流れる電流が変化(時間 Δt の間に ΔI 変化)したとき,電磁誘導により,回路 B に誘導起電力(-M(ΔI/Δt) )が生じる現象である。この時,比例定数 M を相互インダクタンス(mutual inductance)という。 - 自己誘導(self-induction)
閉ループ回路の電流が時間的に変化すると,電流の変化を妨げる向きに回路に逆起電力が生じる現象。 - インダクタンス(inductance)
コイルを流れる電流を変化させたとき電磁誘導によりそのコイル,あるいは他のコイルに発生する起電力の大きさを表わす量をいい,単位には,アメリカの物理学者ヘンリーに因んでヘンリー( H )が用いられる。 - 自己インダクタンス(self-inductance)
自己誘導係数ともいい,自己誘導で生じる起電力の大きさを表わす量(単位 ヘンリー H )で,コイルの巻数,寸法,周囲の媒質によって定まる定数である。
ページの先頭へ
【素子が 1 個のインピーダンス】
ここでは,基本となる回路の素子(抵抗 R ,コイル L ,コンデンサ C )が1個の場合のインピーダンスを示す。
抵抗 R 1 個
抵抗(XR = R )が 1 個の回路のインピーダンス Z は,
Z = XR = R
で与えられ,インピーダンスの大きさ | Z | は,複素数で与えられるインピーダンスの絶対値で,
| Z | = R
となる。
コンデンサ C 1 個
コンデンサ(容量性リアクタンス XC )が 1 個の回路のインピーダンス Z は,虚数 j × j = –1 なので,
![]()
で与えられ,インピーダンスの大きさ | Z | は,複素数で与えられるインピーダンスの絶対値で,
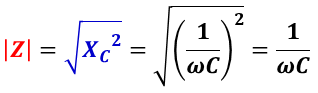
となる。
コイル L 1 個
コイル(誘導性リアクタンス XL )が 1 個の回路のインピーダンス Z は,
Z = XL = jωL
で与えられ,インピーダンスの大きさ | Z | は,複素数で与えられるインピーダンスの絶対値で,
![]()
となる。
ページの先頭へ
【素子が 2 個の合成インピーダンス】
ここでは,回路素子として,抵抗 R ,コイル L ,コンデンサ C のうち 2 個で構成される回路の合成インピーダンス(combined impedance)を示す。
この場合には,直列回路(series circuits)と並列回路(parallel circuits)に分けられる。なお,虚数 j × j = –1 である。
直列回路と並列回路の計算では, 分圧の法則,分流の法則を適用すると容易になる。
RL 直列回路
合成インピーダンス Z は,
![]()
インピーダンスの大きさ | Z | は,
![]()
RL 並列回路
合成インピーダンス Z は,
![]()
インピーダンスの大きさ | Z | は,
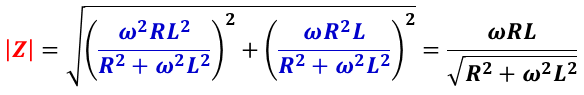
LC 直列回路
合成インピーダンス Z は,
![]()
インピーダンスの大きさ | Z | は,
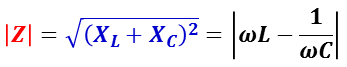
LC 並列回路
合成インピーダンス Z は,
![]()
インピーダンスの大きさ | Z | は,
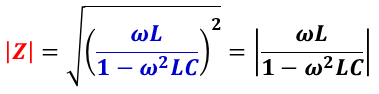
分圧の法則,分流の法則
キルヒホッフの法則(Kirchhoff's laws)から導き出される法則で,直流回路での電圧,電流,抵抗の計算では,下図に例示するように,電流が同じとなる抵抗の直列回路では分圧の法則(voltage divider rule),電圧が同じとなる並列回路では分流の法則(current divider rule)が用いられる。
なお,交流回路では,抵抗を直列回路ではインピーダンス,並列回路ではインピーダンスの逆数のアドミタンス(admittance)で考えると同様の計算が可能である。

分圧・分流の法則,重ね合わせの原理,相反定理説明図
- キルヒホッフの法則(Kirchhoff's law)
ドイツの物理学者グスタフ・ロベルト・キルヒホフ(1824年 ~ 1887年)が発見した法則に対する一般的な呼称であるが,技術分野の異なる次の 3 つの法則がある。
一つは,電気分野の電気回路の電流と電圧に関するキルヒホッフの法則(電気回路)
二つ目は,電磁波分野の黒体放射など局所熱平衡状態で成り立つ,光と物体の相互作用に関するキルヒホッフの法則(放射エネルギー)
三つ目は,熱化学分野の反応熱の温度係数が反応前後の熱容量の差に等しいというキルヒホッフの法則(反応熱)である。 - キルヒホフ(Gustav Robert Kirchhoff)
グスタフ・ロベルト・キルヒホフ(1824年 ~ 1887年)は,プロイセン生まれのドイツの物理学者で,キルヒホッフの法則(電気回路,放射エネルギー,化学反応熱),分光学,音響学で知られる。 - 共振(resonance)
振子などの機械的の場合は,共鳴ともいわれ,振動する物体に固有振動数(固有振動)に近い外力を加えると,その仕事が有効に吸収され,物体の振動が激しくなる現象をいう。
電気的振動の場合は,その電気回路を共振回路(resonance circuit)といい,発振,同調などに利用される。 - 重ね合わせの原理(principle of superposition)
電源を複数持つ線型回路において,電気回路計算に利用される手法のひとつで,重ね合わせの理,重畳の理とも呼ばれる。
線型回路の任意点の電流,任意の点間の電圧は,それぞれの電源が単独に存在していた場合の和に等しい。
計算に際しては,下図に示すように,電源毎に回路を分解して考えるが,この際に電圧源(電圧を一定に保つ低電圧電源)は短絡,電流源(電流を一定に保つ定電流電源)は開放したものと考えてそれぞれを計算する。その後,それらを重ね合わせて元の回路の電圧,電流を求める。 - 相反定理(reciprocal theorem)
可逆定理ともいわれ,二つのものを入れ替えても同等であるということを示す定理である。
相反性は線形回路の中で,電気抵抗(R :レジスタンス),コイル(L :インダクタンス),コンデンサ(C :キャパシタンス)で構成されるなどの限られた適用範囲に適用できる性質ではあるが,回路理論(logic circuit:論理演算を行う電気回路及び電子回路)の基礎的な性質である。
ページの先頭へ
【RLC 直列回路】
ここでは,回路素子として,抵抗 R ,コイル L ,コンデンサ C の 3 個が直列(series)に結ばれた回路である。
合成インピーダンス Z は,
![]()
インピーダンスの大きさ | Z | は,
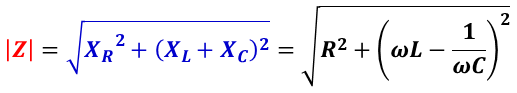
共振周波数
回路に加える交流の周波数を変化させると,合成インピーダンスが変化する。ある周波数になると,インピーダンスの虚数部がゼロ(ωL – (ωC)– 1 = 0 )となり,インピーダンスの極値(抵抗値 R )が得られる周波数になる。
この状態を共振(resonance)という。また,共振する RLC 直列回路は,特に RLC 直列共振回路と呼ばれる。
共振状態のインピーダンスは,Z = R となるので,この時の角周波数ω0 (= 2πf0 )を RLC 直列共振回路の共振周波数という。
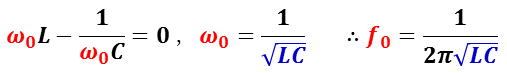
式から分かるように,共振周波数は,コイルの自己インダクタンス L とコンデンサの静電容量 C の値で決まるので,インダクタンスと静電容量の選択で共振周波数を調整することができる。
共振周波数で,インピーダンスが極小となり,回路に流れる電流が極大となる。この回路は,フィルタとよばれ,ある一定の周波数領域の信号だけを取り出したいときなどに使われている。
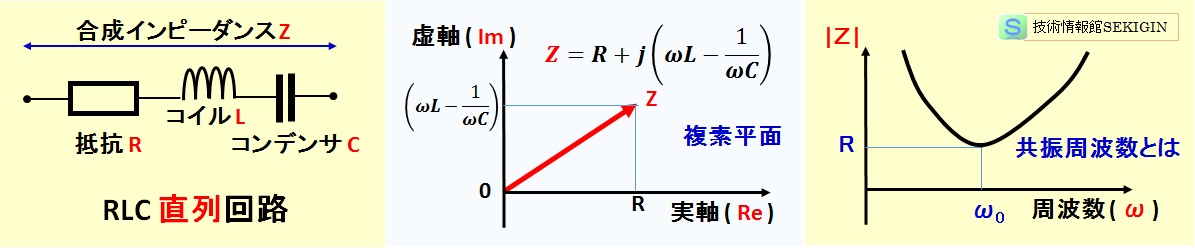
RLC 直列回路の特徴
ページの先頭へ
【RLC 並列回路】
ここでは,回路素子として,抵抗 R ,コイル L ,コンデンサ C の 3 個が並列(parallel)に結ばれた回路である。
合成インピーダンス Z は,
![]()
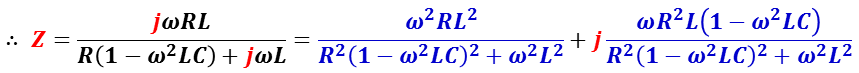
インピーダンスの大きさ | Z | は,
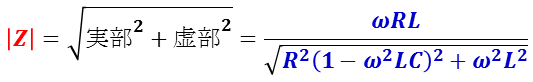
共振周波数
RLC 並列回路の共振では,インピーダンスの虚数部がゼロ( 1 – ω2LC = 0 )で,インピーダンス極大(=抵抗 R ,アドミッタンス極小)になる。この時の角周波数ω0 (= 2πf0 )を RLC 並進共振回路の共振周波数という。
単に共振周波数といった場合は直列回路の共振周波数をいい,並列回路の共振周波数は,並列共振周波数や反共振周波数(antiresonance frequency)といわれる。
反共振周波数ではインピーダンスが極大,すなわちアドミッタンスが極小となり,回路に流れる電流は極小となる。
![]()
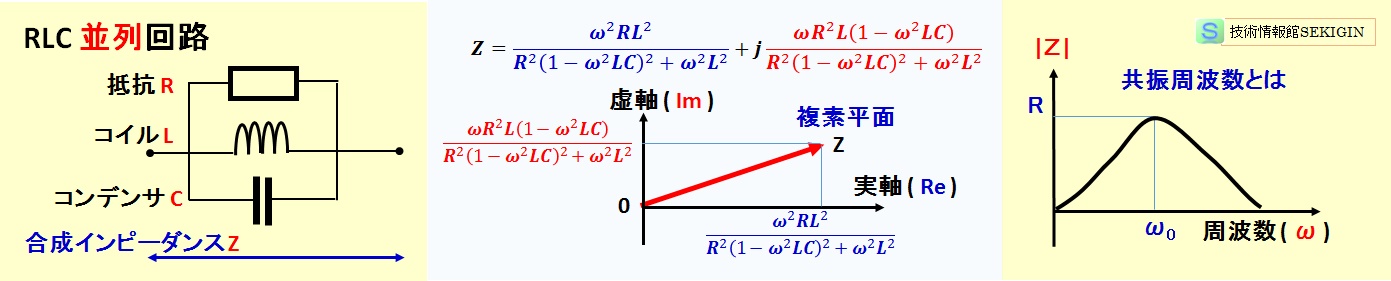
RLC 並列回路の特徴
ページの先頭へ