第四部：無機化学の基礎　無機分析化学(分析とは)

　JIS K 0211 「分析化学用語（基礎部門）： Technical terms for analytical chemistry (General part)」では，
　検量線（ calibration curve , working curve ）
　“物質の特定の性質，量，濃度などとそれらの測定値との関係を表した線。校正曲線ともいう。”
と定義している。

　一般的な測定で得られる値（データ）は，目的の量そのものではなく，間接的な信号量（光の強度，電流量など）の場合が多く，これらの量と目的とする量との対応を得るために検量線が用いられる。
　検量線を得るためには，組成，純度，活性等の明らかな標準物質（ RM ： reference material ，JIS K 8005 「容量分析用標準物質」など）の濃度を変えて得た標準溶液を用い，分析対象物質の測定条件と同条件で測定するの一般的である。

　標準物質（ RM ： reference material ）
　“指定された性質に関して十分に均質，かつ，安定であり，測定又は名義的性質の検査において，意図する用途に適していることが立証されている物質”（ JIS K 0211 「分析化学用語（基礎部門）」）
　標準溶液の濃度範囲は，最小二乗法を用いて直線と近似できる範囲を選択するのが望ましい。直線近似が困難な場合は，適切な曲線に回帰する等の方法を用いることになるが，測定点が少ないと誤差が大きくなる。

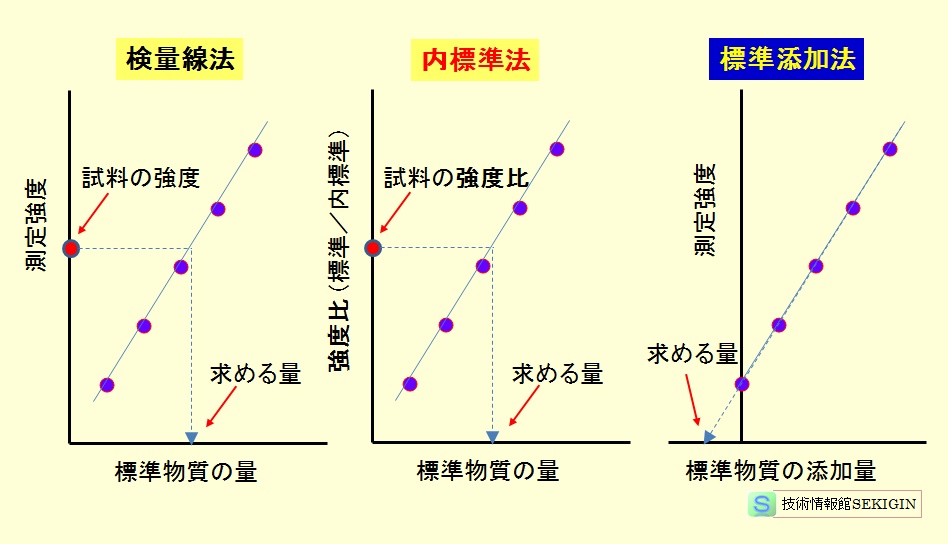
　検量線を用いた定量分析は，検量線法，内標準法，標準添加法に分けられる。

　検量線法（絶対検量線法，強度法）
　分析目的の物質（分析種）の標準物質を用意し，試料の濃度を挟む（内挿値）ように，段階的に濃度を変えた標準物質の溶液（標準溶液）を準備する。なお，試料の濃度が未知の場合は，予備試験で概略の濃度範囲を把握してから準備する。
　標準溶液の性状は，分析試料の性状に近いものを準備する。例えば，分析種以外の物質が多量に含まれているときは，干渉による妨害を相殺するために，これらを添加した標準溶液を準備する。
　化学分析方法に準じて標準溶液を測定し，横軸に分析種の濃度（又は含有率），質量などを目盛り，縦軸に検出器の出力信号などの測定強度を目盛ることによって検量線（校正曲線，校正関数）を作成する。
　分析試料溶液の測定強度と検量線とから試料溶液の分析値を求める。

　内標準法（強度比法）
　検量線法と同様の方法で，濃度の異なる標準溶液を準備する。これらとは別に，分析種と物理的・化学的性質の類似する他の物質の溶液（内標準）を準備する。試料溶液と標準溶液に，同一量の内標準を添加した溶液を分析に供する。
　化学分析方法に準じて標準溶液を分析し，分析種と内標準物質の測定強度比を求める。横軸に分析種の濃度（又は含有率），質量などを目盛り，縦軸に測定強度比を目盛ることによって検量線（校正曲線，校正関数）を作成する。
　分析試料溶液の測定強度と検量線とから試料溶液の分析値を求める。
　内標準法は，適切な内標準の選択で，検量線法に比較して，精度・再現性の向上が期待できる。

　標準添加法
　標準添加法は，検量線法，内標準法での定量分析が困難な試料の分析に適用される方法である。
　全量フラスコなどの体積計に同量の分析試料溶液を入れたものを 5個以上準備する。これに標準溶液をゼロから順次増やして添加する。この時，分析種濃度が適当な間隔で異なる溶液になるように調整する。
　添加した分析種の濃度（ゼロを含む）を横軸に，測定強度又は強度比を縦軸に目盛り，直線近似で結び，その直線を横軸のマイナス方向に延長し，横軸と交差した点の値を読み取る。読み取った値からマイナス記号を取り去った値を分析値とする。

　同じ装置を用い，繰り返し測定した場合，同じ値が得られるとは限らない。細心の注意を払って測定しても，測定値にはある程度の不確かさ（誤差）が含まれる。

　誤差の主な要因
　個人誤差：読み取りミス，記録ミス，有効数値の桁間違い，数値の丸め方の誤りなど
　系統誤差：測定器の許容誤差，機器の調整不良，測定条件のずれ，計器読み取りなどでの観察者のくせ，間接測定による換算時の誤差，近似による解析の誤差など
　偶然誤差：温度，湿度，気圧，電圧，振動などの測定環境の変動
　などがある。
　個人誤差は，二重チェックなどの人的ミスの回避で避けられる。系統誤差についても，機器類の適正な校正・補正，試験室の整備，手順の整備などで誤差を小さくできる。偶然誤差は，確率的な現象のため，測定回数や時間を増やすことで影響を小さくできる。

　一般的には，誤差という場合は，偶然誤差を指すことが多い。なお，真の値（ X ）と測定値（ xi ）の差を絶対誤差（εi = xi – X ）といい，絶対誤差を真の値で除した値を相対誤差という。

　ばらつきの評価
　偶然誤差の分布関数は，正規分布（ガウス分布）となることが多い。
　すなわち，N 個のデータからなる母集団の絶対誤差の分散（σ² ）は，絶対誤差（εi ）の二乗の平均値（ <εi² > ）で定義される。
　　　　　　σ² ＝ <εi² > ＝ ｛ ( x1 – X )² + ( x2 – X )² + ( x3 – X )² + ・・・ + ( xn – X )² ｝/ N
　分散（σ² ）が小さいことは測定精度が高いことを意味し，分散の平方根（σ）は母集団の標準偏差と呼ばれる量である。
　正規分布では, 誤差±σ以内に 68.3 ％，±2σ以内に 95.4 ％，±3σ以内に 99.7 ％が分布する。

　標準偏差の求め方
　実際の測定では，母集団のデータを得られないので，n 個のデータからなる標本を抽出し計算することになる。真の値を知ることができないので，n 個の標本平均（ < x > ）が用いられる。この時，標本の分散（ s² ）は次の通りで，分散の平方根は標本の標準偏差（ s ）といわれる。
　　　　　　< x > = ( x1 + x2 + ・・・ + xn ) / n
　　　　　　s² ＝ ｛ ( x1 – < x > )² + ( x2 – < x > )² + ( x3 – < x > )² + ・・・ + ( xn – < x > )² ｝/ n

　測定値のバラツキの表現には，分散や標準偏差の他に，最大値と最小値の差，偏差 2 乗和（ S = n s² ），不偏分散（ V ），変動係数（ CV ）が用いられる。
　　　　　　V ＝ ｛ ( x1 – < x > )² + ( x2 – < x > )² + ( x3 – < x > )² + ・・・ + ( xn – < x > )² ｝/ ( n – 1 )
　　　　　　CV ＝ s / < x >
　化学分析では，測定値のバラツキを見るのにしばしば CV ％を使う。5 ％以下であれば、その測定値は概ね信用して良いと判断され，10 ％を超えるときはバラツキが大きいと判断される。

　母集団の標準偏差の推定
　母集団の標準偏差が未知のときは，標本の標準偏差から推定することができる。母集団の標準偏差をσ，標本のサイズ n の標準偏差を s とすると，正規分布ならば分散σ² は，自由度 n - 1 のχ² 分布に従う。
　　　　　　χ² ＝ n s² / σ²
　χ² 分布は，データが意味あるものなのかを確認する統計的仮説検定に用いられる。これによると，標本の数 n が大きいほど，s とσの比が小さくなるので，測定回数が多いほどばらつきが小さくなる。
　一般的には，n が大きいほど標本の平均値は，母集団の平均に近づき，n = 5 であれば，偶然誤差の影響が実用上で受けないとされている。厳密には，統計的仮説検定（ F 検定，t 検定，χ二乗検定など）を用いて評価される。

　異常値の棄却や統計的仮説検定は，エクセルソフトで広く出回っているのでこれらを活用するのが良い。