物理 第六部:電磁気学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,電磁波の基本に関し, 【電磁波とは】, 【電磁波の種類】, 【マクスウェルの方程式(微分形)】, 【マクスウェルの方程式(積分形)】, 【電磁波の発生(模式)】 に項目を分けて紹介する。
【電磁波とは】
電磁波(electromagnetic wave)は,電磁放射(electromagnetic radiation)とも呼ばれ,電場と磁場が互いに垂直な方向に変化することで形成される横波(波動)が,空間や物質中を伝わる現象である。
電磁波は,イギリスの物理学者マクスウェルが理論的に予言し,ドイツの物理学者ヘルツにより存在が実証された。その後,光,X線,γ線も電磁波であることが知られた。
電磁波は,その波長(周波数)区分で,電波(長波,中波,短波 HF ,メートル波 VHF ,デシメートル波 UHF ,マイクロ波など),光(赤外線,可視光線,紫外線など),放射線(X線,γ線)に大別される。
電磁波は,波としての性質と粒子としての性質を持つことで知られる。
波としては【物理光学】で紹介した散乱や屈折,反射,また回折や干渉などの現象を起こす。
量子力学的には粒子としても考えられ,例えば,物体が何らかの方法でエネルギーを失うと,そのエネルギーに相当する電磁波が放出される。
粒子としての電磁波と物質の関係
運動する荷電粒子がゼロでない加速度成分をもつ物質からエネルギーや運動量を伝搬できる電磁波が発生する。発生した電磁波は光子(photon)といわれる。
物質と重突した電磁波は,物質中の電子や原子核などの荷電粒子との相互作用(電磁相互作用)の結果として,物質による電磁波の吸収(電磁波のエネルギーが物質の内部エネルギーに変換)と物質による電磁波の散乱が起きる。
なお,電磁波の散乱は,電磁波を吸収した物質中の荷電粒子が加速度運動し,この結果として電磁波を放射することで起きる。
物質の外部へ放射された散乱波は,いわゆる反射波を構成する。物質の内部へ放射された散乱波は,散乱を繰り返しながら物質中を進行する。このため,物質中での電磁波の伝搬速度は,物質の性質を反映して決まることになる。性質の異なる物質との界面での屈折は,両物質中の伝搬速度の違いのために起きる現象である。
電磁波の吸収や散乱などの諸性質は,後述のマクスウェルの方程式系により定量的に導くことができる。特に,真空中での電磁波の挙動は,完全に記述できるといわれる。
物質との相互作用に関しては,真空中におけるマクスウェルの方程式系の拡張解釈となるが,適切な条件,仮定の付加で,巨視的現象については実用的に利用可能な表現が可能と考えられている。
【参考:基礎用語】
- マクスウェル(James Clerk Maxwell)
ジェームズ・クラーク・マクスウェル(1831年~1879年)は,イギリスの理論物理学者。熱力学のマクスウェルの関係式,電磁気学のマクスウェルの方程式,統計力学のマクスウェル分布(マクスウェル・ボルツマン分布)で知られる。 - ヘルツ(Heinrich Rudolf Hertz)
ハインリヒ・ルドルフ・ヘルツ(1857年 ~ 1894年)は,ドイツの物理学者で,マックスウェルの電磁気理論を発展させ,電磁波の放射の存在を初めて実証したことで知られる。周波数の SI 組立単位のヘルツ(Hz)にその名を残す。 - 電磁相互作用(electromagnetic interaction)
ゲージ場理論より,荷電粒子と電磁場(光子)の相互作用で,荷電粒子間に働く作用は光子によって伝搬されると説明される。電磁相互作用を媒介する光子を仮想光子と呼ぶ事もある。
光子の質量がゼロのため,作用の到達距離は無限に長く,電荷(electric charge)を帯びた粒子間,及び磁気を帯びた粒子間の強度が距離の逆二乗に比例するとするクーロンの法則( Coulomb’s Low )として定式化されている。 - 光子(photon)
光量子ともいい,JIS Z 8120「光学用語」では“放射エネルギーの素量(量子)。その値はプランク定数 h と放射の周波数 ν の積に等しい。フォトンともいう”と定義している。 - X線(X-ray)
レントゲン腺ともいわれ,ドイツの物理学者ヴィルヘルム・コンラート・レントゲン(Wilhelm Conrad Röntgen ,1845年 ~ 1923年)が発見した電磁波で,未知の放射線との意味を含み X 線と命名した。
X線の明確な定義はないが,一般的には,波長が紫外線より短くγ線より長い電磁波(100 ~ 0.01オングストローム程度)とされる。
X線には,原子の内殻の軌道電子をはじき出したとき,他の軌道電子が遷移することで発生する特性X線,電子の加速度運動で発生(制動放射)する白色X線などがある。
X線の強い透過力,干渉,回折などの波としての現象を利用し,病気の診断(X線撮影),結晶構造の解析(X線回折),元素分析(蛍光X線分析)などに利用される。 - ガンマ線(gamma ray , γ- ray)
放射線の一種で,放射性元素のγ崩壊で放出される電磁波。明確な定義はないが,波長 10‐11 m 以下の電磁波をいう。一般的な X 線より透過力が大きいが,電離作用は小さい。癌の治療,材質検査などに利用されている。
ページの先頭へ
【電磁波の種類】
電磁波は,周波数により多くの分類がある。分類の詳細は【波長分類と主な用途】で紹介し,ここでは,電波,光,放射線の一般的な分類の概要を紹介する。
電波(radio waves)
ラジオ波ともいわれ,電磁波のうち光より周波数が低い(波長の長い)ものを指す。電磁波の特性や用途の異なる周波数帯で,極超短波からマイクロ波まで分類されている。
極超長波(ultra low frequency):周波数が超長波(VLF)よりも低い,すなわち周波数 3 kHz以下の電波。
極超長波は周波数帯により,周波数 300 Hz ~ 3 kHz の極超長波(ultra low frequency ,ULF),30 ~ 300 Hz の極極超長波(super low frequency ,SLF),3 ~ 30 Hz の極極極超長波(extremely low frequency ,ELF)に分けられる場合もある。
超長波(very low frequency):略語 VLF ,周波数 3 ~ 30 kHz の電波。
長波(low frequency , long wave):略語 LF ,周波数 30 ~ 300 kHzの電波。
中波(medium frequency , medium wave):略語 MF ,周波数 300 kHz ~ 3 MHz の電波。
短波(high frequency , short wave):略語 HF ,周波数 3 ~ 30 MHzの電波。HF は,電離層で反射する。
超短波(very high frequency):略語 VHF ,周波数 30 ~ 300 MHz の電波で,メートル波とも呼ばれる。
マイクロ波(microwave):周波数 300 MHz ~ 3 THz の電磁波。
マイクロ波は,周波数帯により次のように細分される。なお日本語名称には,波長を用いた名称が用いられている。
周波数 300 MHz ~ 3 GHz の極超短波(ultra high frequency ,UHF),周波数 3 GHz ~ 30 GHz のセンチメートル波(super high frequency , SHF),周波数 30 ~ 300 GHz のミリメートル波(extremely high frequency ,EHF),周波数 300 GHz ~ 3 THz のサブミリ波(tremendously high frequency ,THF)に分けられる。
光(light)
赤外線(infrared radiation)は,JIS Z8120 「光学用語」で“単色光成分の波長が可視放射の波長より長く,およそ 1 mm より短い放射。”と定義している。
可視光線(visible radiation)は,JIS Z8120 「光学用語」で“目に入って,視感覚を起こすことができる放射。 光線という概念で用いる場合は可視光線という。一般に可視放射の波長範囲の短波長限界は 360 ~ 400 nm ,長波長限界は 760 ~ 830 nm にあると考えてよい。”と定義している。
紫外線(ultraviolet radiation)は,JIS Z8120 「光学用語」で“単色光成分の波長が可視放射の波長より短く,およそ 1 nm より長い放射。”と定義している。
放射線(radiation)
放射線という場合,高い運動エネルギーを持つ物質粒子(粒子放射線)と高エネルギーの電磁波(電磁放射線)をいう。
電磁放射線(electromagnetic radiation)には,放射性崩壊などで生じる短い波長(0.01 nm 以下)のガンマ線(gamma ray),軌道電子の遷移や電子の加速度運動などで発生する波長 0.001 nm ~ 10 nm 程度の X 線(X-ray)がある。
ページの先頭へ
【マクスウェルの方程式(微分形)】
マクスウェルの方程式(Maxwell's equations)は,電磁方程式(electromagnetic field equations)ともいわれ,イギリスの物理学者マクスウェルが見出した電磁場の時間的・空間的変化を記述する古典電磁気学の基礎方程式である。
マクスウェルの方程式(微分形)は,次の 4 つの微分方程式で構成される。なお,以下に紹介する微分方程式における記号「∇·」,「∇×」は,それぞれベクトル場の発散(div)と回転(rot)を意味する。
磁束保存の式(磁場に関するガウスの法則)
磁場の構造に関する式で,磁力線はどこかを起点とすることも終点とすることもできない,すなわち連続であることを示す式。⇒ 磁荷(モノポール)が存在しないことを示す。
![]()
ここで,B は磁束密度(単位はテスラ T )である。
ファラデー・マクスウェルの式(ファラデーの電磁誘導の法則)
磁場の時間変化があるところには電場が生じることを示すファラデーの電磁誘導の法則の定式化である。
変動磁場がないとき,電場は渦なしで電位(ポテンシャル)が定義できる。時間的に磁場が変動するとき,磁場の方向に垂直な面に電場の渦巻きが発生する。この時,電場の向きは磁場の変化を妨げる方向(レンツの法則)となる。
![]()
ここで,E は電場の強さ(単位はニュートン毎クーロン N/ C ),B は磁束密度(単位はテスラ T )である。
マクスウェル・ガウスの式(電場に関するガウスの法則)
この式は,電荷密度と電場に関する式で,電束が電荷の存在するところで発生・消滅し,それ以外のところでは保存されることを示す。
![]()
ここで,ρは電荷密度(単位はクーロン毎立方メートル C/m3 ),D は電束密度(単位はクーロン毎平方メートル C/m2 )である。
電場の強さ E ,誘電率εとしたとき,電場が非常に強くない限り,電束密度 D と電場の強さ E には D =εE の関係がある。
真空の誘電率ε0 とから微分形のマクスウェル・ガウスの式( E – B 対応)は,
![]()
で表すことができる。
アンペール・マクスウェルの式(電流の磁気作用についてのアンペールの法則)
電場の時間変化と電流とで磁場が生じることを示す式である。式は,電流によって磁場が生じることを示すアンペールの法則に電場の時間変化を加えたものである。
実電流の方向と垂直な面に磁場の渦巻きができる。磁場の向きはフレミングの右手の法則に従う。
![]()
ここで j は電流密度(単位はアンペア毎平方メートル Am–2 ),H は磁場の強さ(単位はアンペア毎メートル A/m ),D は電束密度である。
磁場が非常に強くなく,磁場の強度が小さい範囲では,磁束密度 B ,磁場の強さ H ,透磁率)μの間には,B = μH の関係がある。
真空中では,透磁率μは真空の透磁率μ0 = 4π×10–7 N A–2 で置き換えられるので,
![]()
で表すことができる。
【参考:基礎用語】
- マクスウェル(James Clerk Maxwell)
ジェームズ・クラーク・マクスウェル(1831年~1879年)は,イギリスの理論物理学者。熱力学のマクスウェルの関係式,電磁気学のマクスウェルの方程式,統計力学のマクスウェル分布(マクスウェル・ボルツマン分布)で知られる。 - ファラデー(Michael Faraday)
マイケル・ファラデー(1791年~1867年)は,イギリスの化学者,物理学者で,ファラデーの電磁誘導の法則,ファラデーの電気分解の法則,ファラデー定数など電磁気学,電気化学への貢献で知られる。 - ガウス(Carolus Fridericus Gauss)
カール・フリードリヒ・ガウス(1777年 ~ 1855年)は,ドイツの数学者,物理学者で,近代数学,電磁気学など物理学に多くの業績を残す。 - アンペール(André-Marie Ampère)
アンドレ=マリ・アンペール(1775年 ~ 1836年)は,フランスの物理学者,数学者で,アンペールの法則の発見など電磁気学の創始者の一人とされる。なお,電流のSI基本単位「A:アンペア」はアンペールの名に因んで命名されている。 - 電荷密度(density of electric charge , charge density)
電気量(電荷)の密度をいい,単位体積では体積密度,単位面積では面密度,単位長さあたりでは線密度という。
ページの先頭へ
【マクスウェルの方程式(積分形)】
積分形のマクスウェルの方程式も広く用いられるので,それらを次に示す。
磁束保存の式(磁場に関するガウスの法則)
![]()
ここで B は磁束密度,A は 体積 V を囲む閉2次曲面 で,dA は領域の外側へ向かう方向と直交する閉じた曲面 A 上の微小な方形の領域。
ファラデー・マクスウェルの式(ファラデーの電磁誘導の法則)
ファラデーの電磁誘導の法則から,起電力は磁束の変化の速度に比例(‐𝜕φB/ 𝜕 t )する。
この法則は,コイルを含め任意の閉曲線(閉回路)に適用できるので,閉曲線 C 内の領域を通る磁界の変化とループに沿って発生する電界に比例関係がある。また,φBは磁束保存の式で記述された磁束なので,閉じた曲線の線積分
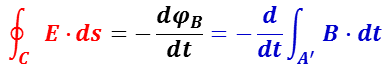
となる。ここでEは誘導電場,ds は閉曲線の微小片,A’ は閉曲線 C を境界とする開 2 次曲面。
マクスウェル・ガウスの式(電場に関するガウスの法則)
ガウスの法則で,電荷の外側へ向かう方向と直交する閉曲面 A 上の微小な方形の領域を dA としたとき,閉曲面当たりの電荷 Q は,
![]()
ここで,ε0 は真空の誘電率である。
なお,電場の強さ E ,誘電率εとしたとき,電場が非常に強くない限り,電束密度 D と電場の強さ E には D =εE の関係がある。
アンペール・マクスウェルの式
微分形式のアンペール・マクスウェルの式の積分形は,
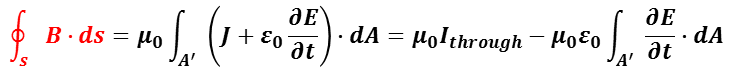
で表される。
B は磁束密度で,磁場が非常に強くなく,磁場の強度が小さい範囲では,磁束密度 B と磁場の強さ H ,透磁率)μの間には,B = μH の関係がある。
μ0 は真空の透磁率, s は開曲面 A の縁となる曲線,J は単位面積に垂直な方向に単位時間に流れる電荷の量(電流密度),ε0 は真空の誘電率,E は電場の強さ。
Ithrough は曲線 s で囲まれた曲面 A を通過する電流
![]()
である。
ページの先頭へ
【電磁波の発生(模式)】
真空中に置かれた導線(アンテナ)に周波数の高い交番電流を流したとき,アンテナから発生する電磁波を模式的に示す。
① 交番電流に応じて,アンテナの周りにアンペールの法則に従い磁場が発生する。磁場は,電流の変動に応じて変動する。磁場の向きは,右手の法則(右ねじの法則)による。
② 磁場も時間的に変動するので,磁場の周辺にファラデーの法則で変動する電場が発生する。なお,電場は,磁場の面に対し垂直な面で,レンツの法則)に従い電場の向きは磁場の変化を妨げる方向を向く。
③ 発生した電場は時間的に変動(変位電流)するため,電場の周辺にマクスウェルの方程式で変動する磁場が発生する。なお,磁場は,電場の面に対し垂直な面で,磁場の向きは電場の変化を妨げる方向を向く。
④ ②に戻りその周辺に電場が発生する。
⇒ 以下②,③の繰り返しにより,磁場と電場が同期した進行波(横波)になる。
このように,進行波は電場誘導と磁場誘導の繰り返しで生じるので,電場のみの波,磁場のみの波は存在できず,電場と磁場の重なる波(互いに垂直な面)が生じる。このため,電場と磁場の両方の波を一緒にした電磁波といわれる。
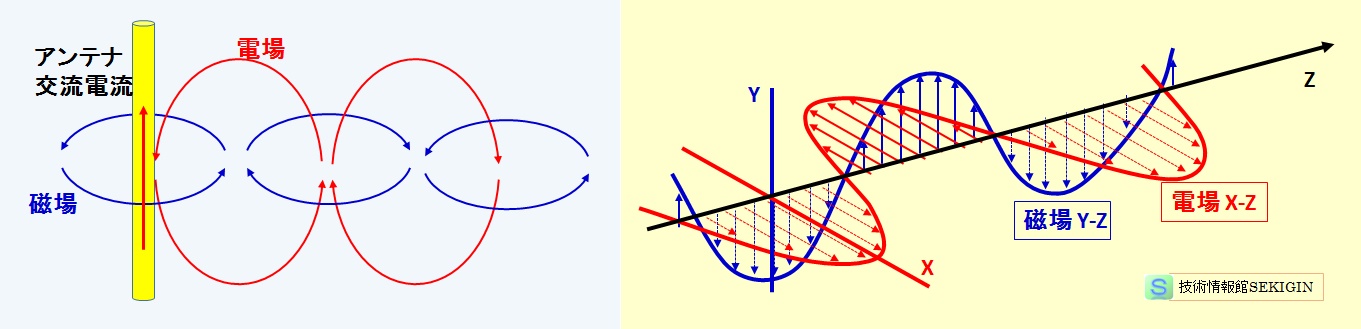
電磁波の発生(模式図)
ページの先頭へ