物理 第六部:電磁気学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,電場の基本に関し, 【電場の中で電荷に働く力】, 【電場の重ね合わせの原理】, 【電気力線,電束】, 【ガウスの法則】, 【帯電体の形状と電場】 に項目を分けて紹介する。
【電場の中で電荷に働く力】
電場(electric field)
工学分野では電界とも呼ばれ,電荷の分布で生じる電気的な力(静電気力)の働く空間(自由電子がない絶縁空間)で,記号 E を用いて表されることが多い。
時間によって変化しない電場を静電場や静電界と呼ぶ。
なお,静電気力(electrostatic force)とは,電荷の間に働く引力や斥力,すなわちクーロン力をいう。
電場内のある 1 点に単位正電荷( 1 C ,クーロン)をおいたとき,これに作用する力をその点における電場の強さ(electric field strength),力の向きを電場の向きという。なお,電場の強さは,電場の向きを含めたニュートン毎クーロン( N/ C )の単位を持つベクトル量である。工学分野では,電場の強さを電界強度(electric field strength)という場合が多い。
なお,日本語のニュアンスが似ているため混用しがちな後述の電束密度(electric flux density)は,電荷により作られる電場を表すベクトル場で,電場の中に置かれた電荷に作用する力を表す電界強度とは定義,単位が異なる。
電場の強さ(電界強度)
電場の強さ E( N/ C )の中で,位置 r に静止する電荷 q( C )に働く静電気力 F( N )は,
F = q E(r)
で与えられる。
この場合,電場の強さの定義により,正電荷の受ける力は電場の向きと一致し,負電荷の受ける力は電場の向きと反対向きとなる。
すなわち,対象とする電場を作る電荷 Q の点電荷からの距離 r の地点の単位正電荷に働く力 F は,電場の定義により,その地点の電荷 Q により作られる電場の強さ E(r) に一致する。
一方で,クーロンの法則( Coulomb’s Low )により,2つの荷電粒子間に働くをクーロン力 ( F ) は,2 つの粒子の電荷の大きさ( q1 と q2 ),粒子間の距離( r ),真空の誘電率 ε0 により,
![]()
で表される。
従って,点電荷 Q からの距離 r の位置における電場の強さ E(r) は,q1 = Q ,q2 = 1 と置いて,
![]()
とできる。
クーロン(Charles-Augustin de Coulomb)
シャルル=オーギュスタン・ド・クーロン(1736年 ~ 1806年)は,フランスの物理学者で,帯電した物体間に働く力を測定からクーロンの法則を発見した。業績に因んで,電荷の単位に「クーロン C 」が用いられている。
ページの先頭へ
【電場の重ね合わせの原理】
複数の点電荷(電荷 Q1 ,Q2 ,・・・ ,Qn ),任意の基準点からの電荷の位置( r1 ,r2 ,・・・ ,rn )とした時,その空間の中のある点の電場 E(r) は,各点電荷の電場のベクトル和として与えられる。
なお,電荷からある点までの距離(スカラー量)は,基準点からある点の位置( r )と基準点から点電荷の位置( ri )までの差( | r – ri | )で与えられるので,ある点の電場 E(r)は,真空の誘電率 ε0 を用いて,
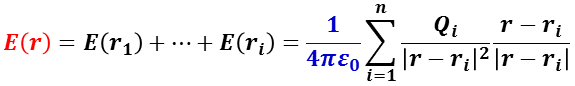
で表される。なお,( r – ri )/ | r – ri | は,電荷 Qi からある点への単位ベクトルを意味する。
ここで,点電荷ではなく,電荷 Q が連続的に分布している物体の場合に,位置 r の電場は,
![]()
となる。ただし,dQ は物体を無限に小さい部分に分割して考えた時の任意の部分の持つ電荷,riはこの部分の位置である。
この関係は,波の重ね合わせの原理(principle of superposition)と同様に,電場の重ね合わせの原理といわれる。
【参考:基礎用語】
- ベクトル(vector)
ベクトルは,有向線分と異なり,平面上の位置に依存せず,大きさと向きだけを持つ量である。
ベクトルには,平面上で方向と大きさで規定される量の平面ベクトルと空間における方向と大きさで規定される量の空間ベクトルに分けられる。単にベクトルという場合は,平面ベクトルを指すのが通例である。 - ベクトル量(vector quantity)
大きさに加え,方向と向きをもつ量で,変位,力,速度,電場,磁場などが例として挙げられる。物理学では,これらの他にもベクトルとして示される量は少なくない。 - 重ね合わせの原理(principle of superposition)
多くの物理系(線形な系)に適用される一般原理で,多数の入力が同時に作用するとき,応答が,それぞれの入力が単独に行われた場合のそれぞれの応答の総和と同等である。
ページの先頭へ
【電気力線,電束】
電気力線(line of electric force , electrical flux line)は,イギリスの化学者,物理学者ファラデーが提案した電気力を視覚的に表現するため,正の電荷から出発して負の電荷で終る仮想的な線をいう。
電気力線は,電場の中の各点での接線が,その点の電場ベクトルの向きと一致する。また,電荷のないところでの途切れ,二つ以上の電気力線の交わりはない。
電気力線は,単に電場の向きを表すだけでなく,その本数に一定の約束をつけることで,電気力線の密度を表すことができる。
例えば,真空の誘電率ε0で,単位正電荷 1 C から発生する電気力線の数を 1/ε0 と定めると,電荷 Q の点電荷から出る電気力線の本数をQ/ε0 とした時,位置 r における電気力線の密度は,半径 r の球の表面積( 4πr2 )当たりの本数と考えることができるので,
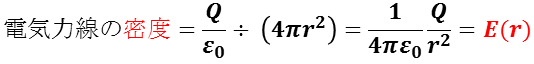
と表せるので,位置 r の電気力線の密度は,電場の強さに比例することが示される。
なお,誘電率εは,次に示すように,電場と電束密度の比例定数として定義されたものである。
電束・電束密度
着目する位置での電気力線の貫通の様子を定量的に規定したものを電束(electric flux)又はフラックスという。
すなわち,上述の例に示すように,定め方により電気力線の数は変わるが,複数の電気力線を束ね,1 (C) の正電荷から 1 本の電束が発生すると定めることで,定量的な表現が可能になる。
この定義では,電束は空間や物体の誘電率に影響されない値になる。
誘電体の中の単位面積当たりの電束を電束密度(electric flux density)や電気変位(electric displacement)といい,記号 D で表す。
上述の例で,電気力線の密度を紹介したが,同様に,点電荷 Q から r 離れた点の電束密度 D は,電束を半径 r の球の表面積で割ったものとなるので,
![]()
となり,電束密度 D は,電荷の存在によって生じる電場 E に比例するベクトル場である。その比例定数εが誘電率と定義される。
電束密度の単位には,クーロン毎平方メートル( C m−2 )が用いられる。
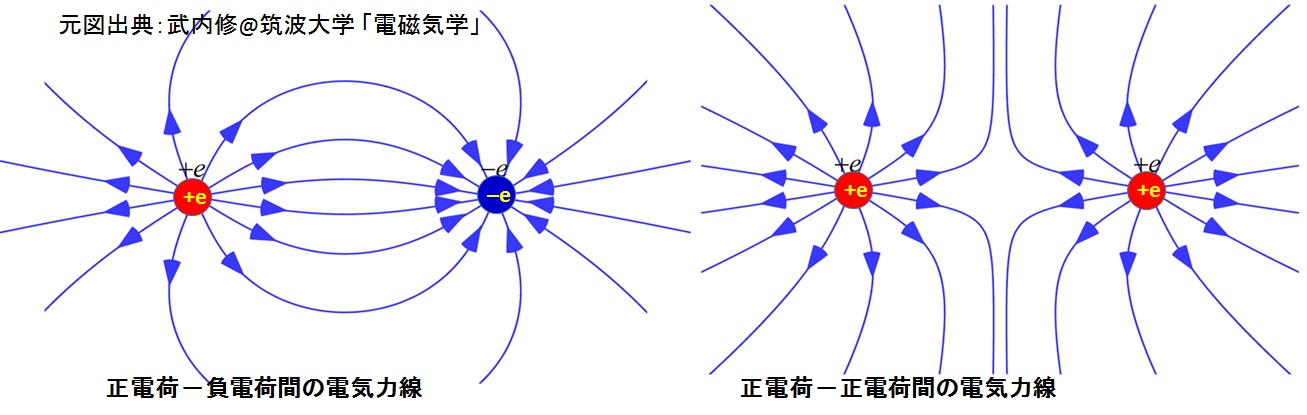
電気力線の模式図
元図出典:武内修@筑波大学 「電磁気学」(2018年当時はフリーアクセス,現在は会員登録必要)
ページの先頭へ
【ガウスの法則】
ガウスの法則(Gauss' law)は,ドイツの数学者,物理学者ガウスが発見した電荷と電場の関係をあらわす方程式で,その後の電気,磁気の基本法則(マクスウェルの方程式)の1つとなった。ガウスの法則は,クーロンの法則(Coulomb’s Low)を時間変化のある場合に一般化したものである。
ガウスの法則では,電場内に想定した曲面の微小部分 dS を垂直に貫く電気力線を考えた時,曲面を通過する電束Ψは,電束密度 D の面積による積分で与えられる。
ここで,電場中の閉曲面(球のみならず任意の形状)を考えると,一般式は閉じた曲線の線積分として
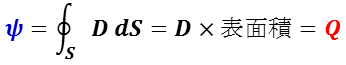
で与えられる。ここで,Q は閉曲面内の全電荷である。式を言い換えると,いわゆるガウスの法則の表現
“電場 E ( = D/ε) の中で任意の閉曲面を通って出ていく全電束 D はその曲面内にある全電荷 Q に等しい。”となる。
ガウスの法則の面積積分を体積積分に直し,divD=ρ (電荷密度)の微分表示を用いたものがマクスウェルの方程式の1つとなる。
マクスウェルの方程式(Maxwell's equations)とは,電磁方程式ともいわれ,イギリスの物理学者マクスウェルが見出した電磁場の時間的・空間的変化を記述する古典電磁気学の基礎方程式で,次の 4 つの微分方程式(法則)で構成される。
○ 磁場の構造に関する磁束保存の式
○ ファラデーの電磁誘導の法則(ファラデー・マクスウェルの式)
○ 電流の磁気作用についてのアンペールの法則(アンペール・マクスウェルの式)
○ 電場および磁場についてのガウスの法則(マクスウェル・ガウスの式)
ファラデー(Michael Faraday)
マイケル・ファラデー(1791年~1867年)は,イギリスの化学者,物理学者で,ファラデーの電磁誘導の法則,ファラデーの電気分解の法則,ファラデー定数など電磁気学,電気化学への貢献で知られる。
ガウス(Carolus Fridericus Gauss)
カール・フリードリヒ・ガウス(1777年 ~ 1855年)は,ドイツの数学者,物理学者で,近代数学,電磁気学など物理学に多くの業績を残す。
マクスウェル(James Clerk Maxwell)
ジェームズ・クラーク・マクスウェル(1831年~1879年)は,イギリスの理論物理学者。熱力学のマクスウェルの関係式,電磁気学のマクスウェルの方程式,統計力学のマクスウェル分布(マクスウェル・ボルツマン分布)で知られる。
アンペール(André-Marie Ampère)
アンドレ=マリ・アンペール(1775年 ~ 1836年)は,フランスの物理学者,数学者で,アンペールの法則の発見など電磁気学の創始者の一人とされる。なお,電流のSI基本単位「A:アンペア」はアンペールの名に因んで命名されている。
ページの先頭へ
【帯電体の形状と電場】
通常の電場の説明では,帯電体として大きさを持たない点電荷を用いて行われることが多い。実際の帯電体は有限の大きさと形状を持つ。ここでは,帯電体の代表的な形状と電場の関係を紹介する。
電束密度・電荷・電場の強さの関係
前述の通りに,電束密度 D は,電場 E と誘電率εとの積で与えられるので,ある閉曲面に垂直な単位ベクトルを n とすると,
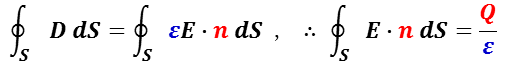
で与えられる。
次には,帯電体が点電荷以外の場合について,電場の強さと形状の関係を紹介する。
帯電球
有限の半径 a を持つ球の内部に電荷 Q が一様の密度で分布している球体を帯電球という。
帯電球の電気力線は,点電荷の場合と同様に,中心から放射状に分布する。従って,電束密度での紹介と同様に,下図左に例示する電荷( Q )を中心とする半径 r の点線で示した球を考え,この球面 S での電場 E を求める。
球面に対しては,すべての電気力線が垂直に通過するので,E・n =| E | とできるので,
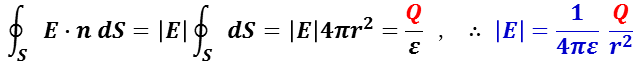
が与えられる。
平板
一定の面密度ρ(単位面積当たりの電荷の量)で電荷が一様に分布している十分に大きい平板の作る電場は,平面の端部付近では歪むが,平板の中央付近では,平板に対して垂直方向の歪みの少ない平行な電気力線になると考えられる。
平板に対して,下図中央に示すように,点線で表す面対称の位置に頂点を持つ直方体の電場 E を求める。
直方体の上面と下面の面積 A したとき, 直方体で囲まれた領域の内部の電荷 Q は,Q = ρA で与えられる。
直方体の側面を貫く電気力線は存在しないので,電場 E の大きさは,上面と下面を貫く成分のみの結果として得られるので,

となり,平面の帯電体の作る電場は,誘電率と電荷の面密度のみで決まる一様な電場である。
直線
電荷の線密度λ(単位長さ当たりの電荷の量)の無限に長い直線状の帯電体では,線に垂直な方向に電気力線が伸びている。
下図右に示すように,点線で表す高さ h ,半径 r の円柱の電荷 Q は,線密度と高さの積( Q = λh )で与えられる。
円柱の上下方向には電気力線が存在しないので,電場 E の大きさは,円柱の側面を貫く成分のみの結果として得られるので,側面積( 2πr h )から
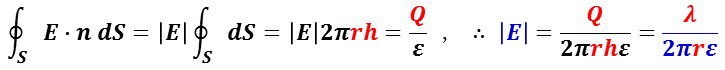
となる。
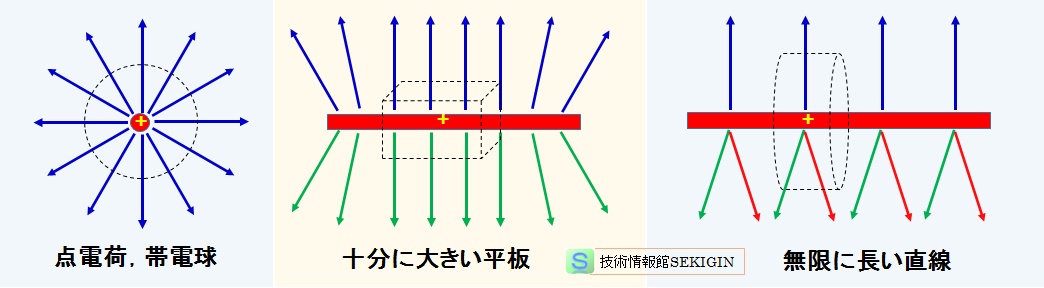
帯電体の形状と電場
ページの先頭へ