第五部:有機化学の基礎 有機化合物の分析
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,赤外線分光の原理に関連し, 【赤外線とは】, 【赤外線の吸収とは】, 【分子運動とは】, 【振動エネルギーの吸収】 に項目を分けて紹介する。
赤外線とは
赤外線( infrared )
単色光(電磁波)成分の波長が可視放射の波長より長く,波長がおおよそ 750nm~1mm と比較的広い波長範囲の光(電磁波)をいう。
赤外線は,波長範囲が広いので,【光の分類】で紹介したように,波長が短く可視光に近い近赤外( 750nm~1.4μm )から短波長赤外( 1.4μm~3μm ),中波長赤外( 3μm~8μm ),熱赤外( 8μm~15μm ),遠赤外( 15μm~1mm )まで,波長範囲で分類される。なお,遠赤外は,マイクロ波の分類とも重なる。
この中で,赤外分光分析法( IR : infrared spectrometry )で利用されるのは,概ね中波長赤外と熱赤外に分類される波長範囲( 2.5μm ~25μm )の光である。
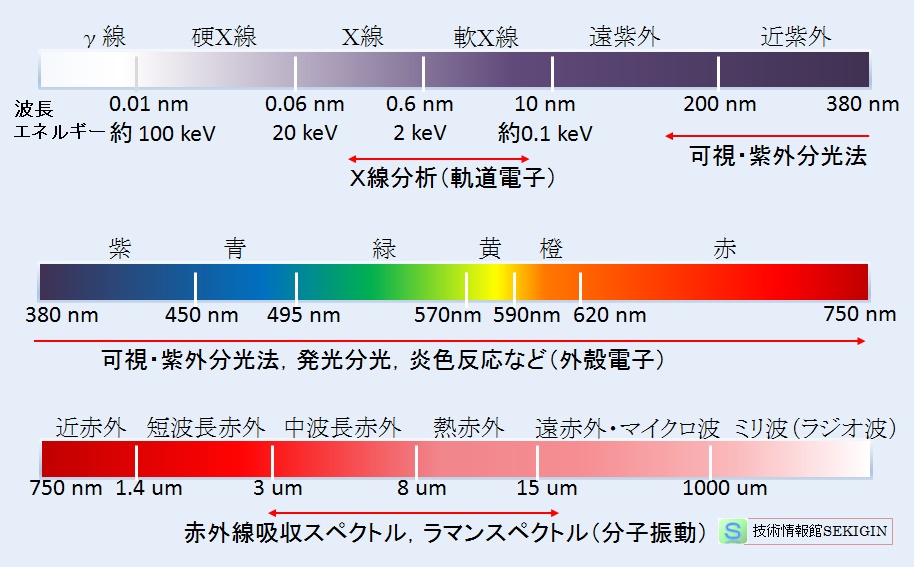
光の波長(エネルギー)区分と分析利用例
ページのトップへ
赤外線の吸収とは
【光の吸収】で紹介したように,光(光子)のエネルギー E ( J )は,プランク定数 h( Js ),周波数ν( s-1 ),波長λ( m ),光の速度 c( m s-1 )とすると,次式で与えられる。
E = hν= h cλ-1
なお,真空中の光速 c = 2.99792458×108 m s-1 ,プランク定数( Planck constant )h = 6.626070040×10-34 Js である。
式から分かるように,周波数νが小さいほど,言い換えると波長λが長いほどエネルギーが低い。すなわち,赤外線は,可視光や紫外線より波長が長く,エネルギーが小さいため,軌道電子の遷移による紫外線や可視光の吸光・発光とは異なる機構で吸収される。
赤外線のエネルギー範囲は,軌道電子の遷移に必要なエネルギーより小さく,分子の運動エネルギーの範囲に相当する。すなわち,分子の運動エネルギー状態の変化により,赤外線の吸光・発光が起きる。
赤外線の吸光・発光
具体的には,分子を構成する軌道電子エネルギー,分子の運動エネルギー(並進,回転,振動)が変化することになる。なお,軌道電子の状態変化には大きなエネルギーが必要で,分子運動の変化は比較的小さいエネルギーで起きる。
一般的には,近赤外線より波長の短い光,すなわち可視光,紫外線,真空紫外線,X線などの持つエネルギーで励起される場合は,軌道電子のエネルギー状態の遷移が起きる。
近赤外線より波長の長い光,すなわちいわゆる赤外線(中波長赤外線,熱赤外線),遠赤外線(マイクロ波)のエネルギーで分子運動(並進,回転,振動)のエネルギー状態が変化する。この中で,次で紹介するように,振動エネルギーの状態変化,すなわち基底状態から励起状態への変化で吸光が,励起状態から基底状態への変化で発光が起きる。
ページの先頭へ
分子運動とは
エネルギーを吸収した分子は,【熱運動】で紹介したように,気体・液体の場合には並進,回転,振動エネルギーが増加し,固体の場合は格子振動エネルギーが増加する。
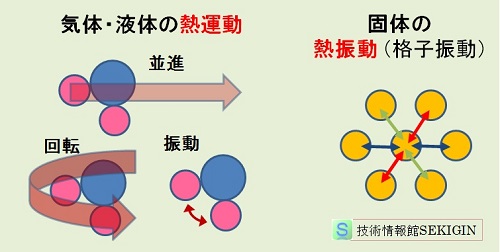
分子・原子の運動
運動エネルギーと温度(熱力学的温度)の関係
並進運動,回転運動のエネルギーは,熱力学的温度(絶対温度)と比例関係にあり,1自由度当たり 1/2kBT のエネルギーが分配される(エネルギー等分配則)。
なお,kB はボルツマン定数( = 1.380 648 52(79)×10-23 JK-1 ),T は熱力学的温度( K :絶対温度)を示す。
エネルギー等分配則( law of equipartition of energy )とは,
“系の持つ自由度ごとに一定量のエネルギーが配分される”
という統計熱力学の一つの法則で,単に等分配則ということもある。
自由度と分子の運動エネルギー
n 個の原子からなる分子は 3n個の自由度を持ち,下図に示す例のように,分子の種別により,次のように自由度が並進,回転,振動の運動に割り振られる。
なお,分子の運動エネルギーは,並進,回転の自由度×1/2kBT であり,振動の自由度に対するエネルギーと分子の運動エネルギーとは区別される。
| 分子の種別 | 自由度 (並進) | 自由度 (回転) | 自由度 (振動) | 運動エネルギー |
|---|---|---|---|---|
| 単原子分子 | 3 | 0 | 0 | 3/2kBT |
| 2原子分子 | 3 | 2 | 1 | 5/2kBT |
| 直線型の3原子分子 | 3 | 2 | 4 | 5/2kBT |
| 非直性の3原子分子 | 3 | 3 | 3 | 3kBT |
| 直線型のn原子分子 | 3 | 2 | 3n-5 | 5/2kBT |
| 非直性のn原子分子 | 3 | 3 | 3n-6 | 3kBT |
振動のエネルギー
振動は,分子内の狭い領域で起きるため,並進や回転と異なる扱いが必要である。
環境温度が十分に高い場合は統計力学でも扱え,1自由度当たり 1kBT (並進,回転の 2 倍)のエネルギーが分配される。
環境温度がさほど高くない場合は,量子力学的な効果を受ける。
すなわち,振動エネルギーは,とびとびのエネルギーしか取れない,温度が低いときは振動運動が基底状態にあり,多少温度が上昇しても励起状態に遷移しないたため,分子運動に対する振動運動の寄与は 0 となる。
すなわち,振動のエネルギー吸収と放出は,軌道電子の場合と同様に,光エネルギーの吸収などによる振動準位間の遷移によって起きる。
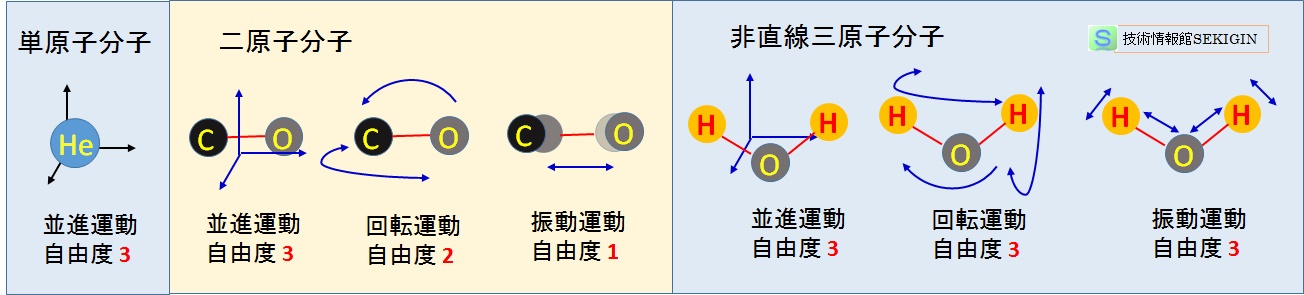
分子運動と自由度(模式図)
ページの先頭へ
振動エネルギーの吸収
振動準位間の遷移は,振動遷移と呼ばれ,主に赤外分光法またはラマン分光法によって観測される。
振動遷移は,振動量子数の変位 ⊿ν=±1 の場合に,振動により双極子の変位がゼロではない場合に赤外線による遷移(赤外線吸収)が起き,分極率の変化がゼロでない場合にラマン効果による遷移(ラマン散乱)が起きる。
分極率( polarizability )とは,原子や分子の電子雲などがもつ電荷分布の相対的な偏りを表す物理量である。
例えば,二原子分子の振動は伸縮振動であるが,等核二原子分子の酸素( O2 )や水素( H2 )は振動での双極子変位が無いので赤外線を吸収しないが,異核二原子分子の塩化水素( HCl )や一酸化炭素( CO )は双極子変位があり赤外線を吸収できる。
振動モード
有機化合物の例として,メチレン基( –CH2– )に見られる許容振動を下図に示す。
伸縮振動( stretching vibration )
2 つの原子の伸縮が同じ方向に起きる対称伸縮( symmetrical stretching )と2 つの原子の伸びと縮みが互いに反対の非対称伸縮( asymmetrical stretching )がある。
変角振動( bending vibration )
3 つの原子で作る面内で結合角が変わる面内変角と面と垂直方向に振動する面外変角に分けられる。また,それぞれには 2 つの原子が同じ方向に動く対称と反対方向に動く非対称に分けられる。
すなわち,対称面内変角(はさみ振動;scissoring ),非対称面内変角(横揺れ振動; rocking ),対称面外変角(縦揺れ振動; wagging ),非対称面外変角(ねじれ振動; twisting )の 4種に分けられる。

振動の種類
ページの先頭へ