第五部:有機化学の基礎 有機化合物の分析
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,赤外分光法に用いる装置に関連し, 【赤外分光光度計とは】, 【光源・検出器】, 【分散素子】, 【干渉計】 に項目を分けて紹介する。
赤外分光光度計とは
赤外分光法( infrared spectroscopy ;IR )
試料に赤外線を照射し,試料を透過又は反射する赤外線を分光することで,赤外線の吸収スペクトルを得て,試料の化学的性状を知る方法である。
吸収スペクトルを得るために用いる赤外分光光度計は,分光方法により,マイケルソン干渉計を用いたフーリエ変換型赤外分光光度計と回折格子などの分光器を用いた分散型赤外分光光度計に大別される。
分散型赤外分光光度計の利用が減り,現在の主流はフーリエ変換型赤外分光光度計( FT–IR )であるが,赤外分光法理解のため,分散型赤外分光光度計を含めて,JIS K 0117 「赤外分光分析方法通則: General rules for infrared spectrophotometric analysis 」を参考に,装置の基本構成,光源,分光器,干渉計などを紹介する。
装置の基本構成
分散型赤外分光光度計は,光源部,試料部,分光測光部(減光器,セクターミラー,分光器,検出器,増幅器),データ処理部,表示・記録部などで構成される。
フーリエ変換型赤外分光光度計は,光源部,試料部,分光測光部(干渉計,検出器,増幅器,A /D 変換器,サンプリング信号発生器),フーリエ変換部,データ処理部,表示・記録部などで構成する。
分光器( spectrometer )
一つの光源からの光を波長分散させて一つの焦点面上に波長順に結像させる機器をいい,スリット,ミラー,分散素子などから構成される光学系である。
分散素子( dispersive device )とは,種々の波長成分の光を含む光を波長ごとに分けるための光学素子で,プリズム,回折格子,又はそれらを組み合わせた光学系が用いられる。
また,分散素子によって単一波長の光を取り出す機器は,モノクロメータ( monochromator )ともいわれる。
干渉計( interferometer )
光の干渉を利用して光路差などを測定する機器をいい,マイケルソン干渉計,マッハ・ツェンダー干渉計,フィゾー干渉計などがある。
以下では,主な光源と検出器,分光器に用いられる分散素子, FT–IR で用いる干渉計を紹介する。
ページのトップへ
光源・検出器
主な光源
古くはネルンスト灯( ZrO2 ,CeO ,ThO2 ),グローバー灯( SiC )が用いられていた。最近の装置では,高輝度セラミック光源,タングステン・ヨウ素ランプ,ハロゲンランプ,タングステン・重水素ランプ,水冷式高圧水銀光源などが用いられている。
なお,FT–IR の干渉図形測定におけるサンプリング信号発生器には,通常の光源には He–Ne レーザのパルスが用いられる。
干渉図形( Interferogram )とは,マイケルソン干渉計からの信号を光の光路差を横軸に,光の強度を縦軸にとって示した図形をいい,インターフェログラムともいう。
赤外線の検出器
古くは熱電対,サーミスターなどの温度で抵抗値の変化する材料を用いたボロメータ(高感度の電気抵抗温度計)が使用されていた。
最近の FT–IR では,内部光電効果を示すテルル化カドミウム水銀( HgCdTe : MCT )検出器,または焦電効果を示す硫酸トリグリシン( (NH2CH2COOH)3·H2SO4 : TGS ),この水素イオンを重水素化した重水素化トリグリシン硫酸結晶( DTGS )などが検出器に用いられている。
TGS は,室温で動作し,透過率や反射率の高い試料など光量の多い赤外光の測定に適するが,反射法での測定など光量の少ない赤外光を高感度で検出するためには,MCT が用いられる。
なお,MCT は低温で動作するため,液体窒素冷却が必要となる。
赤外吸収が非常に強く,通常の透過法や反射法での測定が困難な試料の場合は,光音響検出器を備えた光音響分光法が用いられる。
【参考】
光電効果( photoelectric effect )
物質が光を吸収して自由電子(伝導電子を含む。)を生じる現象で,電気伝導度の増加又は起電力が表れる内部光電効果と,固体表面から光電子が放出される外部光電効果とがある。
フォトダイオードなどの光電流発生の説明に用いる光起電効果( photovoltaic effect )とは,用語は似ているが,定義が異なるので誤用に注意する。
焦電効果( pyroelectric effect )
温度変化で誘電体の分極(表面電荷)が変化する現象である。焦電体は圧電効果も示すので,圧電体の一種でもある。
ページの先頭へ
分散素子
分光器に用いられる代表的な分散素子には,プリズムと回折格子がある。
プリズム( prism )
光を分散・屈折・全反射・複屈折を目的に,周囲の空間と屈折率の異なる透明な媒質でできた多面体をいう。
媒質の屈折率 n は,真空中での光の速度( C )と媒体中での光の速度(ν)との比,n = C /νで表される。
光は電磁波のため,媒質を透過する際に,媒質の電子と相互作用し,媒質の誘電率と分極の影響を受け,媒質中の光の速度が遅くなる。この影響は,光の波長が短いほど大きくなるため,屈折率は,短い波長ほど大きくなる。
従って,屈折率は,媒質の特性と光の波長に依存する。
比較的波長の短い可視光の分光には,ガラスや石英で出来たプリズムを用いることができる。しかしながら,波長の長い赤外線領域の電磁波は,ガラスや石英などでできた一般的なプリズムでは吸収される。
そこで,波長の長い赤外線に対しては,金属塩のプリズムが用いられる。一般的な赤外線用プリズムには,臭化カリウム( KBr ),ふっ化カルシウム( CaF2 ),塩化ナトリウム( NaCl ),臭化タリウム( TlBr )などの金属塩が用いられる。使用する塩の選択は,分析に使用する波長領域により決められる。
回折格子( diffraction grating )
回折( diffraction )とは,水の波(波紋),空気の波(音),電磁波(ラジオ波,光,X線,γ線),粒子の波(電子線,中性子線)などの媒体を伝わる波が,障害物によりその背後に回り込む現象をいう。
障害物が多数存在する場合は,それぞれで回折した波の衝突が起き,ある場所では波が弱め合い,異なる場所で強め合う干渉( interference )が起きる。
回折格子とは,格子状のパターンによる回折を利用して干渉縞を作るために使用される光学素子の総称である。
格子パターンは,直線状の凹凸がμm サイズの周期で平行に並ぶ構造の物が多い。材質,凹凸の厚みや凹凸の周期などは,用途や使用する波長域で異なる。
吸光光度計などの分光に用いる回折格子(ブレーズド回折格子)では,特定波長の回折の次数 n の回折角θm ,回折格子の格子の溝の間隔 d ,入射光の入射角度θ0 とすると,回折光の波長λとに,次の関係にあることが知られている。
nλ= d ( sinθm ± sinθ0 )
すなわち,格子の溝の間隔 d ,波の入射角度θ0 を固定し,スリットを用いて角度θm を変えながら測定することで,回折光の波長λと強度を検出できる。
なお,X線回折法では,用いるX線の波長λを固定し,波の入射角度θ0と角度θm を測定することで,結晶構造の格子面の距離 d を求めるている。
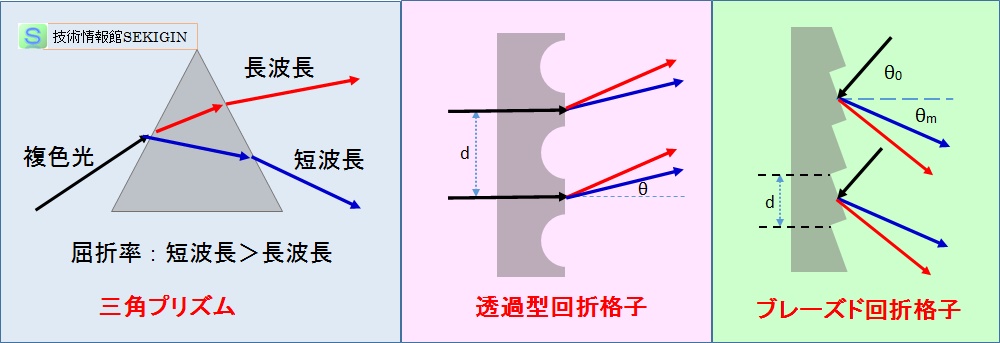
分散型分光器の例
ページの先頭へ
干渉計
光の干渉効果で得られた干渉縞をフーリエ変換することで光スペクトルに変換することができる。前述の分光器に比較して,高い波長分解が得られ,光の利用率が高い特徴がある。
干渉計には,大きく分けて多光束干渉計を用いるものと 2 光束干渉計を用いるものとがある。フーリエ変換型赤外分光光度計では,2 光束干渉計であるマイケルソン干渉計が用いられている。
マイケルソン干渉計( Michelson's interferometer )
最も一般的な干渉計で,ビームスプリッタを用いて光束(光のビーム)を 2 つに分割し,反射させた後,再び合流させることで干渉させる。
2 つの光の経路長を変化させたり,経路上の物質を変えたりすることで種々の干渉縞を生成できる。
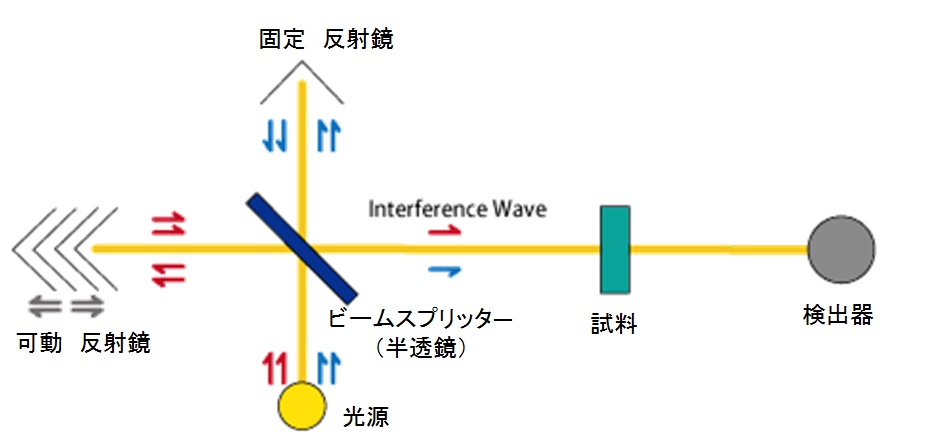
2 光束干渉計と FT – IR 装置基本構成(透過法)
元図出典:日本分光(株)FTIRの基礎
半透鏡と 2 枚の反射鏡(固定鏡,可動鏡)で構成される干渉計に平行光束(レーザー光)が導かれ,半透鏡で 2 つの光束に分割される。
2 つの光束は,固定鏡と可動鏡で反射され半透鏡に戻り再び合成されることで干渉波を発生する。この時,可動鏡の位置(光路差)で異なる光の干渉波が得られる。
可動鏡の位置別の干渉波の信号強度をフーリエ変換することで,周波数成分毎の光の強度に分離し,赤外スペクトルが得られる。
分散型と比較した FT–IR のメリットとして,分散型では測定困難な遠赤外や可視領域までの広い測定領域に対応可能,スキャンが不要なため多波長の同時検出が可能,強度の高い光の利用や信号の積算による S /N 比の向上,可動鏡の可動域を変えることで高い波長分解能が得られるなどが挙げられる。
【参考】
フーリエ変換( Fourier transform )
フーリエ分解ともいい,与えられた関数を別の周期関数に分解して表現する際に用いられる数学的手法で,ある信号に含まれる周波数成分の解析,通信・画像処理などの実用分野で広く利用される。
ページの先頭へ