第五部:有機化学の基礎 有機化合物の分析
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,核磁気共鳴(NMR)分光に関連し, 【核磁気共鳴とは】, 【磁気モーメントとスピン量子数】, 【磁場の中の原子核】, 【核磁気共鳴の原理】, 【共鳴周波数】, 【核磁場共鳴分光スペクトル】 に項目を分けて紹介する。
核磁気共鳴とは
核磁気共鳴( nuclear magnetic resonance : NMR )
外部静磁場に置かれた原子核が固有の周波数の電磁波と相互作用する現象をいう。
これを利用した核磁気共鳴( NMR :nuclear magnetic resonance )分光分析法( spectroscopy )は,有機化学で利用できる最も有効な分光法で,有機化合物の構造決定の際に最初に頼る手法でもある。
有機化学では,化合物の構造を知るために,水素原子の核磁気共鳴分光分析を用いるのが通例である。他に,ふっ素( 19F ),りん( 31P )及び炭素( 13C )の核磁気共鳴分光からそれらの元素周りの構造研究にも活用されている。
ここでは,核磁気共鳴の原理を中心に紹介する。
【参考】
核磁気共鳴画像法( magnetic resonance imaging : MRI )
医療検査で利用される核磁気共鳴画像法( MRI )は,核磁気共鳴において共鳴の緩和時間がその原子核の属する分子の運動状態を反映することを利用したものである。すなわち,生体を構成している水分子の運動状態が,体内の臓器により異なるため,断層撮影法と組み合わせることで,体内の臓器の形状を知ることができる。
ページのトップへ
磁気モーメントとスピン量子数
【原子の構造】で紹介したように,軌道電子は,電荷を持ち,取り得る量子状態に,主量子数,方位量子数,磁気量子数,スピン量子数が割り当てられている。
原子核も電子と同様に,電荷を持ち,量子論的に回転(自転)していると考え,核の周りに磁場が発生し,量子化された角運動量・磁気モーメントを持つと考えられる。すなわち,磁気量子数とスピン量子数が割り当てられる。
原子核の磁気モーメント
陽子と中性子は逆の全角運動量を持つ対を形成するという核構造のモデルによると,核の磁気モーメントは,陽子と中性子の数により次の様に整理されている。
○ 陽子と中性子の数が共に偶数である核の磁気モーメントは,ゼロである。
○ 陽子と中性子の数の一方が偶数で他方が奇数である核の磁気モーメントは,奇数の方の残った不対陽子又は不対中性子の磁気モーメントとなる。
○ 陽子と中性子の数が共に奇数である核の全磁気モーメントは残った不対陽子と不対中性子の磁気モーメントの組み合わせになる。
スピン量子数
スピン量子数とは,粒子固有の角運動量(スピン角運動量)を特徴づける量子数で,半整数( 1/2,3/2 ,5/2 など±整数/2 )又は整数( 1 , 2 , 3 など)を採る。
なお,半整数の値を採る粒子をフェルミ粒子,整数の値をとる粒子をボーズ粒子という。
【原子の構造】で紹介したように,電子はフェルミ粒子で,2 つのスピン量子数 1/2 ,–1/2 を採る。
原子核のスピン量子数
原子核のスピン量子数は,核スピンともいい,量子力学的に求められるが,ここでは,一般的な関係を紹介する。すなわち,原子番号(陽子数)と質量数(陽子+中性子数)の関係から次のように整理される。
なお,有機化合物の核磁気共鳴分光法で利用される代表的な原子の核スピン量子数も併せて紹介する。
1 :原子番号が奇数の場合
a :質量数が奇数
陽子数が奇数で中性子数が偶数となり,スピン量子数は, 1H(1/2) ,15N(1/2) ,19F(1/2) ,31P(1/2) ,35Cl(3/2) ,37Cl(3/2) など半整数値の核スピンを持つ。
b :質量数が偶数
陽子数,中性子数とも奇数で,スピン量子数は, 2H(1) ,14N(1) など整数値の核スピンを持つ。
2 :原子番号が偶数の場合
a :質量数が奇数
陽子数が偶数で中性子数が奇数となり,スピン量子数は, 13C(1/2) ,17O(5/2) など半整数値の核スピンを持つ。
b :質量数が偶数
陽子数,中性子数とも偶数で,12C(0) ,16O(0) ,32S(0) などスピン量子数は,ゼロである。
【参考】
同位体の天然存在比
水素: 1H ( 99.985 %),2H( 0.0149 %),炭素: 12C ( 98.893 %),13C( 1.107 %),窒素: 14N ( 99.6337 %),15N( 0.3663 %),酸素: 16O ( 99.759 %),17O( 0.0374 %),18O( 0.2039 %)
ふっ素: 19F ( 100 %),りん: 31P ( 100 %),硫黄: 32S ( 95 %),33S( 0.76 %),34S( 4.22 %),塩素: 35Cl ( 75.77 %),37Cl( 24.23 %)である。
ページの先頭へ
磁場の中の原子核
前節で紹介したように,原子番号と質量が共に偶数の原子は,磁気モーメントと核スピンが共に ゼロ である。
従って,この原子以外の原子は,核スピン,磁気モーメントともゼロ以外の値を持ち,小さな磁石と仮定できる。
磁気モーメントのエネルギーは量子化されおり,磁気量子数 mⅠで表わされる。磁気量子数は,核スピンⅠの核は磁場中で 2Ⅰ+ 1 個(= –Ⅰ,–Ⅰ+1 … 0 …Ⅰ–1 ,Ⅰ)のエネルギー状態(配向)を取ることができる(ゼーマン効果)。例えば,核スピンⅠ= 1/2 で 2つ,Ⅰ= 1 で 3 つ,Ⅰ= 3/2 で 4 つのエネルギー状態に分裂することになる。
通常は,核スピンがランダムな方向を向いている。ランダムな方向を向く普通の磁石を磁場の中に置くと,磁石のN極は北を指すように磁場方向に整列する。
核スピンを持つ原子の場合は,磁場をかけると整列するが,その磁場方向を向くものと反対方向を向くものに分かれる。
この結果として,強い静磁場を作用させることで,核スピンの向きがそろうことで,全体として磁場をかけた向きに巨視的磁化( macroscopic magnetization )ができるという。
核スピンの「磁石」は,通常の磁石と異なり,外部磁場によりゼーマン効果で分離したエネル―状態により,磁場の方向と同じ向き(平行)に整列するものと反対方向に向くもの 2種類に分かれる。
磁場に平行に配向する核は,反対方向に向く核よりわずかに低いエネルギーを持ち,数もわずかに多い。エネルギー差は,外部磁場の強さに依存する。
静止磁場で配向した 2 種の核は,外部から電磁波を与えると,電磁波のエネルギーを吸収,又は放出で状態(方向)を変えることができる。
この核スピンのエネルギーの吸収・放出を観測する手法が,核磁気共鳴( NMR )分光分析法( nuclear magnetic resonance spectroscopy )である。
【参考】
ゼーマン効果( Zeeman effect )
1896 年にオランダの物理学者 P. ゼーマンの発見した原子から放出される電磁波のスペクトルが磁場中で複数に分裂する現象から,磁場中でのエネルギー順位の分裂現象をいう。
一般には,主量子数 n と方位量子数 l が等しく,磁気量子数 ml だけが異なる軌道電子が,磁場の存在で,磁気量子数と磁場の積に比例して軌道エネルギーの縮退が解けて分裂することになる。このようにスピン角運動量を無視して軌道角運動量のみを考えたときの分裂を正常ゼーマン効果という。
多くの原子の場合には,より複雑なスペクトル線の分裂が見られる。このスピン角運動量と軌道角運動量の両方を考慮した場合の分裂を異常ゼーマン効果という。
電子のスピン角運動量と軌道角運動量がカップリングする結果,より複雑なエネルギー準位の分裂が起こることが原因と分かった。このスペクトル線の分裂はNMRやMRIなどに応用されている。
ページの先頭へ
核磁気共鳴の原理
外部磁場の影響
磁場の中の原子核で紹介したように,原子核のエネルギー状態は,スピン量子に応じて,下図に示すように,外部磁場で分裂する。
例えば,水素( 1H )は核スピンⅠ=1/2 なので,外部磁場中に置かれた水素原子核は 2 つ( =2Ⅰ+1 )のエネルギー準位に分裂する。分裂した準位間のエネルギー差(⊿E )は,外部磁場の大きさ( B0 )のみに依存する。
磁気モーメントμとすると,エネルギー差⊿E は,水素( 1H )の核スピンⅠ= 1/2 なので,次式で表される。
⊿E =μB0/Ⅰ= 2μB0
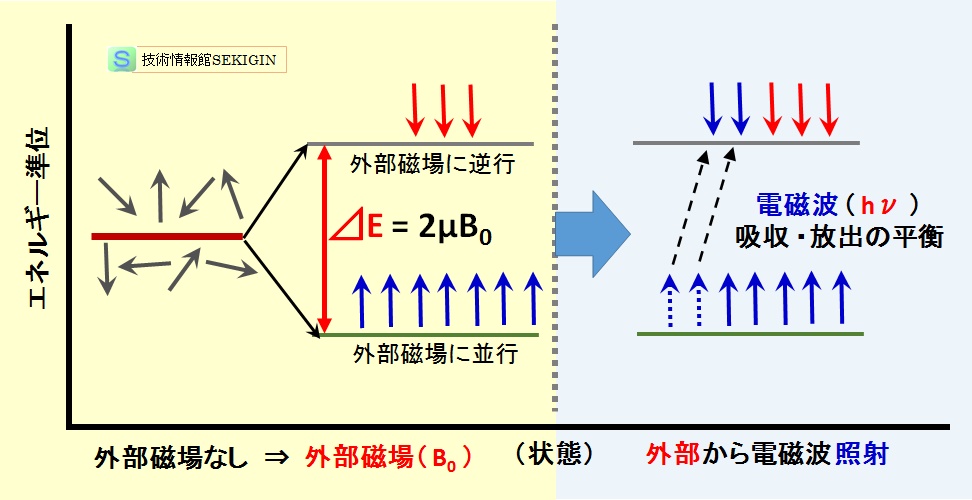
核磁気共鳴の原理
外部磁場を加えた状態で,準位間のエネルギー差(⊿E )に相当する電磁波( hν)を照射すると,上図に示したように,一部の核の遷移が起こる。この時の周波数νを共鳴周波数という。
共鳴周波数の電磁波を照射し続けると,ついには両準位の核が同数となる。その後は,吸収と放出の平衡で両準位の数に変化は見られない。この状態に至った時を飽和と呼ぶ。また,電磁波の照射を停止することで,元の状態に戻る。なお,飽和に至ると NMR 測定が不可能になる。
ページの先頭へ
共鳴周波数
磁気モーメント(μ)は,磁気回転比(γ)とスピン角運動量(Ⅰh /2π)とに次の関係がある。
μ=γⅠh /2π
磁気回転比( gyromagnetic ratio )とは,物理学において,角運動量に対する磁気双極子モーメントの割合をいう。
前述の準位間のエネルギー差(⊿E )に関する式とから,磁気回転比(γ)とエネルギー差には次の関係が成立する。
⊿E =μB0/Ⅰ= γB0 h/2π
一方で,外部磁場に置かれた磁気モーメントを持つ核は,自転している考えられ,重力場に置かれたコマの様に首振り運動(ラーモア歳差運動という)をする。
ラーモア歳差運動( Larmor precession )
電子,原子核,原子などの粒子の持つ磁気モーメントが外部磁場によって歳差運動(首振り運動)を起こす現象をいう。
ラーモア歳差運動は,核磁気共鳴( NMR ),電子スピン共鳴( EPR ),強磁性共鳴( FMR )などの現象にとって重要な概念である。
外部磁場( B0 ),磁気回転比(γ)とした時,回転運動の角周波数(ω)はラーモア周波数( Larmor frequency )と呼ばれ,次式で表される。なお,磁場中でのラーモア周波数を共鳴周波数とも呼ぶ。
ω=γB0
すなわち,エネルギー準位間のエネルギー差(⊿E)との関係は,
⊿E=μB0 /Ⅰ=γB0 h/2π=ωh/2π
となり,角周波数ωと周波数νとの関係 ω=2πν より,
⊿E=hν
が得られる。
すなわち,外部磁場の強度に比例して分裂したエネルギー準位のエネルギー差は,ラーモア周波数の光子(電磁波)の持つエネルギーと一致する。
【参考】
ラーモア歳差運動( Larmor precession )
外部磁場に置かれた磁気モーメントを持つ核は,自転している考えられ,重力場に置かれたコマの様に首振り運動(歳差運動という)をする。このように,電子,原子核,原子などの粒子の持つ磁気モーメントが外部磁場によって歳差運動を起こす現象をアイルランドの物理学者ジョゼフ・ラーモアにちなみラーモア歳差運動といわれる。
ラーモア(Joseph Larmor)
ジョゼフ・ラーモア(1857年 ~ 1942年)は,イギリスの物理学者で,著書『エーテルと物質:Ether and matter 』,磁場中の電子の歳差運動で知られる。
ページの先頭へ
核磁場共鳴分光スペクトル
外部磁場に置かれた原子核に対してラーモア周波数と同じ周波数で回転する回転磁場をかけると磁場と原子核の間に共鳴が起こる。この共鳴現象が核磁気共鳴と呼ばれる。
下図には,外部から回転磁場をかけた時の歳差運動,回転磁場を除去した時の緩和過程について模式的に示した。
図左(励起過程)
強力な静磁場(超電導磁石など)に対して,垂直な面内に設置したコイルに,ラーモア周波数に一致させた周波数の交流電流( RF )を流して回転磁場を加える。
これにより,巨視的磁化 M が,静磁場( B0 )の方向を中心に回りながら,エネルギーの吸収と共に次第に傾いてゆく。
回転磁場を与えるコイルとは別にコイルを設置し,回転磁場の吸収量を測定することで核磁場共鳴分光スペクトルが得られる。
図右(緩和過程)
交流電流を止めると,くるくる回りながら,エネルギーを放出しつつ静磁場の方向へ戻る。
M の傾きの大きさ(フリップ角)は,回転磁場をかける時間で決まるので,その時間を調節することで M を任意の角度にでき,その回転磁場を RF パルスという。
外部磁場に対して垂直方向( 90°)のフリップ角を持たせるための RF パルスを特に 90°パルス,外部磁場と反対向き( 180°)のフリップ角を持たせるためものを 180°パルスという。
RF パルスで倒された M は静磁場の方向を中心に回転するので,その付近にコイルを設置することで,交流電流として信号が得られる。
90°パルスを加えた後,回転磁場を止めることで,観測される信号の振幅が時間とともに減衰する。この現象を自由誘導減衰( free induction decay : FID )と呼ぶ。
回転磁場を与えるコイルとは別にコイルを設置し,RF パルスを与えた後に測定された自由誘導減衰をフーリエ変換することで吸収スペクトルを得る方法をフーリエ変換 核磁気共鳴分光分析法( FT NMR )という。
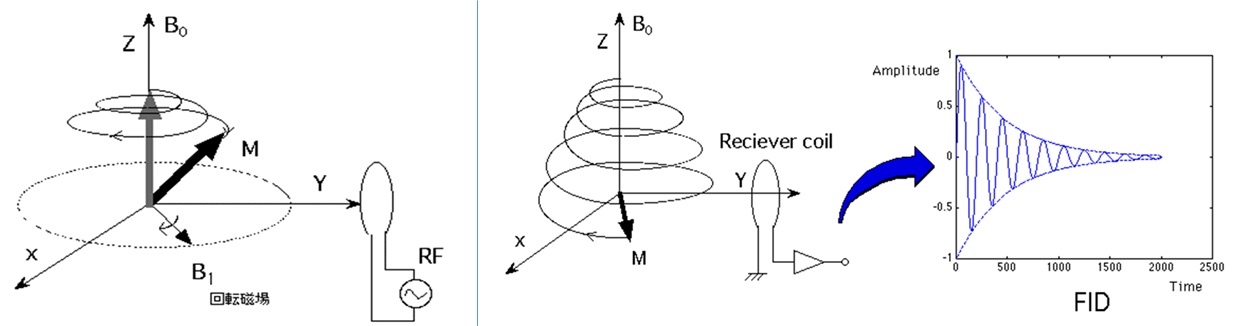
核磁気共鳴(歳差運動)と緩和模式図
図出典:金沢工業大学 先端電子技術応用研究所樋口研究室
ページの先頭へ