物理 第六部:電磁気学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,磁場の基本に関し, 【磁気と磁性】, 【基本用語】, 【磁場とは】, 【磁性体】, 【原子構造と磁性】, 【磁性の種類】 に項目を分けて紹介する。
【磁性と磁気】
磁性(magnetism)は,磁石に特有な他の物質に対して引力や斥力を及ぼす物理的性質をいう。
磁性は,電流の中の電子の運動(電磁気)や量子力学的な電子の軌道運動やスピンで生じる。
磁性の強さは,原子を構成する電子,原子核の磁気モーメント(magnetic moment)によって特徴づけられるが,電気の電荷に相当する磁荷(magnetic charge)は未だに発見されていない。
Magnetism の語源
古代ギリシアのマグネシア地方に産する鉱石が鉄片をひきつけるという奇妙な性質をもっていたので,これがマグネット(magnet :磁石)と呼ばれ,その性質について命名されたといわれている。
磁石の語源
中国で磁鉄鉱が釘を吸着する様子から,慈しんで抱く石から慈石と呼ばれ,後に,磁石になったといわれている。
Magnetisim とは
日本語では,磁性の他に磁気とも訳される。明確な区別はないが常磁性,強磁性,反磁性など物理的性質を意味する場合は磁性を用いる場合が多く,磁気は電磁気,核磁気など磁性によって生じる特性やこれによる現象などに用いられる場合が多い。
次には,英訳に magnetism を含む用語の例を紹介する。
磁性
強磁性(ferro magnetism),常磁性(para magnetism),反磁性(dia magnetism),超常磁性(superparamagnetism), 異常磁性(anomalous magnetism),動的磁性(dynamic magnetism),界面磁性(interface magnetism),アモルファス磁性(amorphous magnetism),磁性形成(magnetism formation)など
磁気
電磁気(electro magnetism),核磁気(nuclear magnetism),地磁気(geo magnetism),残留磁気(residual magnetism),誘導磁気(induced magnetism),磁気特性(magnetism property),動物磁気(animal magnetism),高温磁気(high-temperature magnetism)など
形容詞(magnetic)を用いる用語には,磁性と訳する例は少なく,磁気と訳する場合が多い。
magnetic を含む用語の日本語約の例
磁性
磁性原子(magnetic atom),磁性合金(magnetic alloy),磁性細菌(magnetic bacteria)など
磁気
磁気モーメント(magnetic moment),磁気力(magnetic force),磁気双極子(magnetic dipole),磁気加速(magnetic acceleration),磁気作用(magnetic action),磁気浮上(magnetic levitation), 磁気増幅器(magnetic amplifier),核磁気共鳴(nuclear magnetic resonance),磁気異方性(magnetic anisotropy),磁気異常(magnetic anomaly)など
ページの先頭へ
【基本用語】
磁極(magnetic pole)
磁石の強磁性体を引き付ける性能の最も強い点をいう。磁石は必ず1対の磁極をもち,それぞれ正極・負極という。
地球磁場では,北に引かれるほうを正極(N極,北極),南に引かれるほうを負極(S極,南極)とする。
磁荷(magnetic charge)
電荷に対応する磁荷は発見されていないが,磁極の帯びている磁気の量(単位ウェーバ)を磁荷,磁気量,磁極の強さとして扱われる。この時,N 極の磁荷を正,S 極の磁荷を負と定義される。
これは,磁荷をもちいることで,電磁気学の計算が簡単になる利点があるため,道具として使われている。実際に観測される磁気は,磁荷によるものではなく電荷の移動(電子の運動)によるものである。
磁気力(magnetic force)
磁力ともいわれ,磁荷 m1 の粒子(磁極)と距離 r の位置にある磁荷 m2 の粒子(磁極)間に働く力 F で,クーロンの法則の電荷を磁荷に置き換えた形で書くことができる。
すなわち,真空の透磁率μ0 とすると,
![]()
で表される。
単位磁荷とは
真空の透磁率は,μ0 = 4π×10–7 N A–2 で与えられるので,磁極間の距離 r = 1 m のとき,磁気力の大きさ F = (4π)–2×107 N となる磁荷を 1 ウェーバ( Wb )と定められる。
なお,磁荷の単位を SI 基本単位で表すと Wb = kg m2 s–2 A–1 = N m A–1 となる。
透磁率(magnetic permeability)
導磁率ともいわれ,磁場の強さ H と磁束密度 B との間の関係を B = μH で表した時の比例定数μである。
透磁率の単位は H/ m (ヘンリー毎メートル),又は N/ A2(ニュートン毎平方アンペア)で与えられる。
真空の透磁率μ0 と真空の誘電率ε0 と真空中の光速 c との間には
![]()
の関係がある。
真空の透磁率:μ0 = 4π×10–7 N A–2
真空中の光速: c = 2.99792458×108 m s–1
真空の誘電率:ε0 = 8.854×10–12 A2 s2 N−1 m−2
である。
主な SI 単位及び SI 組立単位
磁場関連の主な物理量とその記号,及び SI 単位を紹介する。
磁場(の強さ)H ,磁化 M
アンペア毎メートル: A・m‐1
磁荷 Qm ,磁束 φ
ウェーバ (weber) : Wb = V・s = m2・kg・s‐2・A‐1
磁束密度 B ,磁気分極 Pm
テスラ (tesla) : T = Wb・m‐2 = kg・s‐2・A‐1
透磁率 μ
ヘンリー毎メートル:H・m‐1= m‐1・V・A‐1・s = m・kg・s‐2・A‐2 =N・A‐2
磁場に対応する電場関連の主な物理量とその記号,及び SI 単位を紹介する。
電場(の強さ)E
ボルト毎メートル: V・m‐1
電荷 Q ,電束 ψ
クーロン (coulomb) :C = s・A
電束密度 D ,電気分極 P
クーロン毎平方メートル: C・m‐2 = s・A・m‐2
誘電率 ε
ファラッド毎メートル: F・m‐1= C・V‐1・m‐1 = m‐3・kg‐1・s4・A2
【参考】
クーロン(Charles-Augustin de Coulomb)
シャルル=オーギュスタン・ド・クーロン(1736年 ~ 1806年)は,フランスの物理学者で,帯電した物体間に働く力を測定からクーロンの法則を発見した。業績に因んで,電荷の単位に「クーロン C 」が用いられている。
ウェーバー(Wilhelm Eduard Weber)
ヴィルヘルム・エドゥアルト・ヴェーバー(1804年 ~ 1891年)は,ドイツの物理学者で,磁気の測定器具などの開発で電磁気学に大きく貢献し,磁束の SI 単位「ウェーバ」に名を残した。
ヘンリー(Joseph Henry)
ジョセフ・ヘンリー(1797年 ~ 1878年)は,アメリカの物理学者で,イギリスの物理学者マイケル・ファラデーと同時期に電磁誘導の発見,自己誘導現象の発見などで知られ,インダクタンスの SI 単位ヘンリーに名を残した。
電荷(electric charge)
素粒子の持つ性質の一つである。電荷の量を電気量(quantity of electricity)や電荷量(quantity of electric charge , charge quantity)という。
なお,電気量や,電荷を持つ粒子そのものを電荷と称する文献,参考書,解説なども少なくなくない。
電荷を持つ粒子(電子や陽子など)を荷電粒子(charged particle),大きさを無視できる理想化された荷電粒子を点電荷(point charge)という。
誘電率(permittivity)
電媒定数ともいい,電束密度と電場の強さとの比をいうが,一般に誘電率といった場合は,誘電体の誘電率を真空の誘電率でわった比誘電率(dielectric constant , relative permittivity)を指すことが多い。
誘電率は。誘電体の誘電分極が生じる程度を表す物質定数,すなわち,外部から電場を与えたとき,物質内の原子や分子の応答の程度を表す。
基本的なの SI組立単位
ボルト (volt) V = W・A‐1 = m2・kg・s‐3·A‐1 :電位差 (電圧)・起電力
ヘンリー(henry) H = V・A‐1・s = m2・kg・s‐2・A‐2 :インダクタンス( L )
ファラド (farad) F = C・V‐1 = m‐2・kg‐1・s4・A2 :電気容量(静電容量 C )
ニュートン (newton) N = m・kg・s‐2 :力
パスカル (pascal) Pa = N・m‐2 = m‐1・kg・s‐2 : 圧力・応力
ジュール (joule) J = N・m = m2・kg・s‐2 : エネルギー・仕事・熱量
ワット (watt) W ¬= J・s‐1 = m2・kg・s‐3 :仕事率・工率・放射束
ページの先頭へ
【磁場とは】
磁場(magnetic field)
磁界ともいわれ,磁石や電流により作られる磁気力の作用する空間を指す。これは,静電気力がおよぶ空間を電場(electric field)というのと同様に,磁気力がおよぶ空間をいう。
磁場の強さ
磁場の強さは,単に磁場ともいうが,単位磁荷( 1Wb)の磁極(正極)を置いた時に受ける力(ベクトル量)をいう。磁場の強さの単位は,ニュートン毎ウェーバ( N/ Wb = A m–1 )となる。なお,磁場の強さの SI 単位はアンペア毎メートル(A/ m)である。
磁場の強さのスカラー量を磁場の大きさといい,力の向き,すなわち磁場の向きは,磁極が正極(N極,北極)の場合は磁場と同じ方向で,負極(S極,南極)の場合は反対向きになる。
従って,磁場 H(単位 N/ Wb = A m–1 )の中に置かれた磁極 m(単位 Wb)の受ける磁気力のベクトル F (単位 N )は,
F= m H
で表される。
磁力線と磁束密度
電気力線と同様の考えに基づき,磁場内において,各点における磁場(ベクトル)の接線方向に一致する曲線を磁力線(line of magnetic force)という。ある点における磁力線の密度はその点における磁場の強さに比例している。
棒磁石のつくる磁力線は,正極( N極)から負極( S極)に向う曲線として示される。
ある点における磁場の強さと方向を,1 Wb を 1 本とした磁力線の束で表したものを磁束(magnetic flux)や磁気誘導束という。
磁束の単位面積当たりの面密度を磁束密度(magnetic flux density)といい記号 B で表される。磁束密度の SI 単位はテスラ( T ),又はウェーバ毎平方メートル( Wb m–2 )が用いられる。
磁束密度と磁場の強さの関係
磁場の強さ H と磁束密度 B との関係は,
H = (μ0 )–1 B - M
で表される。
ここで,μ0(真空の磁化率)で,M は磁場により磁性体内に生じた分極を意味し,磁化(magnetization)や磁気分極といわれる値である。
磁化 M は,磁化された磁性体中の微小な部分における一定に分極した双極子の密度 N ,磁気モーメント m としたとき,M=Nm で与えられる。
ページの先頭へ
【磁性体】
磁性体(magnetic material ,magnetic substance)
磁石を近づけたとき,磁気力の方向と平行に磁化する常磁性(para magnetism)を持つ常磁性体(para magnetic substance),反対方向に磁化する反磁性(dia magnetism)を持つ反磁性体(dia magnetic substance),及び鉄鋼,磁鉄鉱などの物質自身が容易に磁化する強磁性(ferro magnetism)を持つ強磁性体(ferro magnetic substance)に分けられる。一般的に磁性体という場合は,強磁性体のみを指すことが多い。
なお,磁極が比較的簡単に消失,反転する磁性体は軟質磁性体と呼ばれ,容易に変化しない磁性体は硬質磁性体とも呼ばれる。
常磁性(para magnetism)
外部磁場が無いときには磁化を持たず,外部磁場を印加するとその方向に弱く磁化する磁性を指す。
後述するように,常磁性を持つ物質の原子や分子の不対電子のスピンによる磁気モーメントを持っている。外部磁場がない場合は,熱ゆらぎによりバラバラな方向を向いているが,外部磁場が加えられることで,磁場の方向に配向する。
反磁性(dia magnetism)
外部磁場をかけたとき,物質が磁場とは逆の向きに磁化される現象である。この現象は,超電導体で顕著であり,磁気浮上式鉄道(リニアモーターカー)の浮上の原理に用いられている。
原子・分子中の対電子は,弱い反磁性を必ず生み出す。すなわち,全ての物質が反磁性を有している。
これは,運動している荷電粒子に磁場をかけると,ラーモア歳差運動(Larmor precession)により,外部磁場とは逆の磁気モーメント(反磁性)を持つためである。
反磁性は非常に弱く,常磁性や強磁性の原因である不対電子のスピンによる磁性の影響が勝るため,反磁性が顕在化する物質(超伝導体,ビスマス,ダイヤモンド・炭素,銅,鉛,水銀,銀,水など)は少なく,超伝導体(ニオブスズ合金,ニオブチタン合金,銅酸化物高温超伝導体など)以外の多くは非磁性物質として扱われている。
なお,反磁性体は,強磁性体と異なり,自発磁化をもたず,磁場をかけた場合にのみ反磁性の性質が表れる。
強磁性(ferro magnetism)
磁場をかけるとその方向にきわめて強く磁化し,磁場を取去っても残留磁化(residual magnetization)を示す性質をいう。
強磁性を示す単体は,原子番号 26 の鉄( Fe ),原子番号 27 のコバルト( Co ),原子番号 28 のニッケル( Ni ),18 ℃以下の原子番号 64 のガドリニウム( Gd )と少ない。
これらの原子を含む物質では,不対電子を持つことで磁気モーメントが生じる。また,隣り合うスピンが同一方向を向いて整列し,全体として大きな磁気モーメントを持つことができる。

強磁性体の磁化
磁化していない強磁性体 ( a ) , 外部磁場 ( H ) を加えると,磁区間の磁壁が移動し,外部磁場と同じ方向の磁区が成長 ( a ) ,外部磁場がある強さ以上で達する磁区の飽和状態 ( c )
元図出典:物質・材料研究機構(NIMS) 磁性・スピントロニクス材料研究拠点( 2018年参照の図,2021年時点で改変)
磁性体に外部磁場をかけたとき,後述するように,磁性体の中の磁区が磁気的に分極(磁壁の移動で向きが揃う)して磁石になる現象を磁化や磁気分極(magnetic polarization)と呼ばれる。
磁化という場合には,上記の他に,磁性体の磁化の程度を表す物理量(磁場の強さと同じ単位アンペア毎メートル: A・m‐1)としても用いられる。
自発磁化(spontaneous magnetization)
強磁性体(単体では鉄 Fe ,コバルト Co ,ニッケルNi )の他に,反強磁性体(一酸化マンガン MnO ,酸化クロムⅢ Cr2O3 などの化合物),フェリ磁性体(マグネタイト Fe3O4 などの Fe 系の磁性材料)は,外部磁場が無くとも,転移温度以下では自発的に磁化をもっている。これを自発磁化という。
自発磁化は,不対電子のスピン間の交換相互作用によりスピンが平行あるいは反平行にそろうことに起因して起きる。自発磁化の方向は異方性エネルギーが最小となる方向である。
残留磁化(residual magnetization)
磁性体(強磁性体など)に外部磁場を加え,その後に磁場を取り除いても磁性体に残留する磁化をいう。
磁区(magnetic domain)
磁気モーメントがすべて平行に並び自発磁化した小さな領域の集合とみなされる強磁性体で見られる現象である。この自発磁化をもつ領域を磁区という。
【参考:基礎用語】
- ラーモア歳差運動( Larmor precession )
外部磁場に置かれた磁気モーメントを持つ核は,自転している考えられ,重力場に置かれたコマの様に首振り運動(歳差運動という)をする。このように,電子,原子核,原子などの粒子の持つ磁気モーメントが外部磁場によって歳差運動を起こす現象をアイルランドの物理学者ジョゼフ・ラーモアにちなみラーモア歳差運動といわれる。 - ラーモア(Joseph Larmor)
ジョゼフ・ラーモア(1857年 ~ 1942年)は,イギリスの物理学者で,著書『エーテルと物質:Ether and matter 』,磁場中の電子の歳差運動で知られる。
ページの先頭へ
【原子構造と磁性】
物質の構成粒子は,最小単位の素粒子(elementary particle)であるが,一般的には,化学,物性の側面からは,原子(atom)と考えてよい。
原子は,原子核(atomic nucleus)と軌道電子(orbital electron)で構成されている。
原子核による磁化
水素以外の原子核は,正の電荷を持つ陽子(proton)とほぼ同じ質量で電荷を持たない中性子(neutron)がいくつか集まってできている。
原子核は,電荷を持ち,量子論的に回転(自転)していると考えられるので,核の周りに磁場が発生し,量子化された角運動量・磁気モーメントを持つ。
原子核の磁気モーメントは,陽子と中性子の組み合わせにより異なる。陽子と中性子の数が共に偶数の場合の磁気モーメントはゼロとなる。陽子又は中性子の何れかが奇数の場合は,不対陽子又は不対中性子による磁気モーメントを有する。共に奇数の場合は,不対陽子と不対中性子の磁気モーメントの組み合わせになる。
原子核の磁気モーメントと核スピンがゼロ以外の場合は,外部から強い静磁場を作用させると,核スピンの向きが揃い巨視的磁化(macroscopic magnetization)が起きる。
ちなみに,外部磁場により生じる原子核の磁気モーメントのエネルギー状態の配向,すなわちゼーマン効果(Zeeman effect)を利用した核磁気共鳴(nuclear magnetic resonance : NMR )は,有機化合物の定性・定量分析,臨床検査などに利用されている。
軌道電子による磁化
物質の磁性は,原子を構成する軌道電子の影響を強く受ける。軌道電子は,負の電荷を持ち,原子核の周りを運動していると同時に,自転している。
電子の運動や自転によりその周りに磁気モーメントが生じる。これをスピン磁気モーメントと呼ぶ。すなわち,電子一つ一つが微小な磁石として作用する。
なお,電子一個の軌道運動で発生する磁気モーメントは,磁気モーメントの最小単位でボーア磁子(Bohr magneton)と呼ぶ。
電気的に中性の原子では,原子核の周りに,陽子と同数の電子が,主量子数( main quantum number ) n ,方位量子数( azimuthal quantum number ) l (エル) ,磁気量子数( magnetic quantum number ) m で指定されるエネルギー準位の軌道で運動している。
パウリの排他原理(Pauli principle)により, 1 つの軌道には異なるスピン角運動量( spin wave function :上向きのスピン,下向きのスピン)の2つの電子しか入れない。このため,大部分の電子は対電子となり,電子の自転による磁気モーメントは,スピンが打ち消しあうことで,物質の磁気モーメントに寄与しない。また,軌道運動による磁気モーメントも複数の軌道からの打ち消しの効果で物質の磁気モーメントへの寄与が小さい。
しかしながら,鉄( Fe )などの d 軌道が閉殻(電子で埋まっている)となっていない遷移金属では,フントの法則(Hund's rule)により,対になっていない電子(不対電子)が 1 ~ 5 個存在する。例えば,26 番元素の鉄は,4d 軌道に 6 個の電子を持つが,そのうち 4 個の電子が不対電子である。不対電子があると,電子のスピンにより磁気モーメントの合計がゼロにならない。
【参考:基礎用語】
- ボーア磁子(Bohr magneton)
電子の磁気モーメントの基本単位で,記号μB で表す。電気素量 e ,プランク定数 h ,電子の静止質量 me とした時,μB = eh/ 4πme = 9.274×10-24 J・T-1(ジュール毎テスラ)である。デンマークのニールス・ボーアによって再発見されたためボーア磁子と命名された。 - ニールス・ボーア(Niels Henrik David Bohr)
ニールス・ヘンリク・ダヴィド・ボーア(1885年 ~ 1962年)は,デンマークの理論物理学者で,ボーアの原子模型,ボーアの量子条件,ボーア半径,ボーア磁子などの業績により量子論の育ての親として知られる。 - パウリの排他原理(Pauli principle)
パウリにより提唱された原理で,排他律あるいは禁制原理などとも呼ばれる。「 2つ以上のフェルミ粒子は,同一の量子状態を占めることはできない。」と表現され,一つの原子内では,2 個以上の電子が同時にエネルギー・スピンなどの同じ状態をとることはないことを示す原理である。 - パウリ(Wolfgang Ernst Pauli)
ヴォルフガング・エルンスト・パウリ(1900年 ~ 1958年)は,スイスの物理学者で,スピンの理論,パウリの排他原理の発見など現代化学の基礎を築く業績で知られる。 - フントの法則(Hund's rule)
原子のエネルギー準位に関する次の三法則(経験則)をいう。
第一法則:同じ電子配列から生じる状態の中では,多重度の大きいものほど安定となる。
第二法則:同じ電子配列で同じ多重度をもつ状態の中では,軌道角運動量の大きいものほど安定となる。
第三法則:微細構造の中で外殻電子が半分以下しか満たされていない場合は,全角運動量の量子数が小さいものほど安定となるが,半分以上電子が充てんしているときは,全角運動量量子数の大きいものほど安定となる。
ページの先頭へ
【磁性の種類】
d 軌道や f 軌道が閉殻となっていない原子は,不対電子のスピンによる磁気モーメントを持つ。スピンは互いに影響しあい同じ方向を向く強い相互作用が働く。
温度が高い場合には,熱運動の影響がスピン相互作用に勝り,スピンが互いに勝手な方向を向く。この状態に外部磁場をかけると磁性を示すので,常磁性といわれる。
なお,一般的に常磁性材料という場合は,常温(室温付近)でこの状態となる磁性材料をいう。
温度が高くない場合には,スピン相互作用の影響が表れ,下図に示すように,磁気モーメントが規則的に配列する強磁性,反強磁性,フェリ磁性,不規則に配列する常磁性の 4 種類に分類される。
強磁性(ferromagnetism)
強磁性体では,磁気モーメントが同一方向に配列するように交換相互作用(exchange interaction)が働く。分かり易く解説すると,スピン A に近接するスピン B , C , D , E があり,スピン B , C , D が上向きで,スピン E が下向きのとき,スピン A が上向きにするような磁場ができるように作用する。
この考え方は,フランスの物理学者 P.ワイスが提唱した分子場(molecular field ,分子磁場,平均場ともいう)の考え方である。
これにより,A の平均のスピンが上向きになる。ついで,E を中心に考えると,A による分子場によって,E のスピンも上向きをとる傾向が増す。結果として,ある一定の温度(キューリー温度)以下では,ほとんどのスピンが一定の方向を向くようになる。
前述の消磁状態のように,強磁性体が全体として磁化していない場合は,磁性体が数多くの磁区と呼ばれる区域(幅 0.1 mm 程度)に分かれ,それぞれの磁化方向が打ち消され,外に対して磁気作用が現れないためである。
磁区間の境目を磁壁といい,外部磁場が作用すると,磁壁のスピンが反転し,外部磁場の方向と同じ方向の磁区が成長する方向に磁壁が移動する。この結果,強磁性体は全体として外部磁場の方向に磁化する。
室温で強磁性を示す単体には,鉄(Fe),コバルト(Co),ニッケル(Ni)などである。
反強磁性(antiferromagnetism)
反強磁性体では,交換相互作用が隣り合う原子の磁気モーメントを反対方向に配列させるように作用する。結果として,全体として磁性を持たない物質となる。
互いに磁気モーメントが打ち消し合うので,磁気モーメントの配列に規則性があっても自発磁化は消失する。このような物質を反強磁性と呼ぶ。
反強磁性体には,酸化マンガン(MnO),酸化ニッケル(NiO),マンガン,クロム,ランタノイド元素などが挙げられる。
フェリ磁性(ferrimagnetism)
フェリ磁性体では,反強磁性のように,物質中にある方向のスピンと逆方向(ほぼ逆方向)のスピンの 2 種類が共存しするが,一方のスピンが優勢なため,全体として磁化を持つ。
フェリ磁性を持つ物質の代表は,マグネタイト(Fe3O4)のようなフェライトと呼ばれる Fe 系の磁性材料がある。
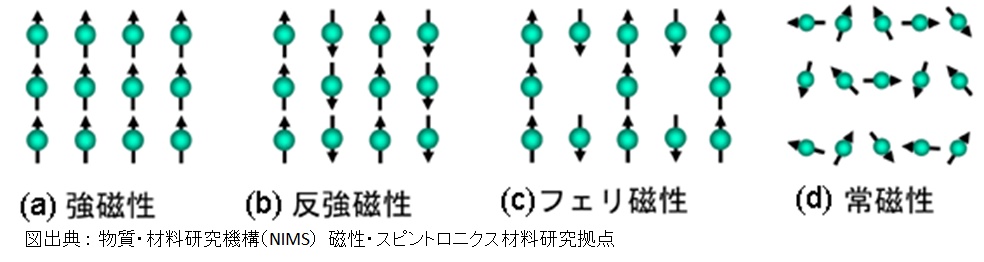
磁性の種類
元図出典:物質・材料研究機構(NIMS) 磁性・スピントロニクス材料研究拠点( 2018年参照の図,2021年時点で改変)
- 交換相互作用(exchange interaction)
物質の磁性を理解するための中心的な概念の一つで,原子のスピン間や異なる軌道上の電子間に働く見かけ上の相互作用をいう。
磁性の担い手である電子の磁気モーメントは,電子のスピンに依存する。すなわち,電子のスピンの向きがそろうと,磁気モーメントの向きがそろい,強磁性が発現する。
このような電子のスピンの向きをそろえるような,同種粒子間に働く量子力学的効果を交換相互作用という。 - 分子場(molecular field)
強磁性理論の初期において,ワイスが導入した磁区の生成を説明するための分子磁場の概念をはじめに,しだいに拡張され,平均場または有効場ともいわれるようになった。分子場は,1つの要素と他の要素との相互作用をこの要素に働く有効な外場と考えて,多体問題を一体問題で近似(平均場近似)する理論である。
ワイスの分子磁場では,孤立した原子は外部磁場によって磁気モーメントを帯びるが,磁性体の中では原子が磁気モーメントを帯びると,これに比例する分子磁場を周囲の原子に及ぼすと考える。 - ワイス(Pierre Weiss)
フランスの物理学者ピエール・ワイス(1865 ~ 1940年)は,分子磁場(分子場)の提唱者,キュリーの法則を拡張したキュリー・ワイスの法則で知られる。 - キュリー温度(Curie temperature)
強磁性体の加熱で永久磁化を失い,常磁性体に変化する転移温度をいう. - P.キュリー(Pierre Curie)
ピエール・キュリー(1859年 ~ 1906年)は,フランスの物理学者で,結晶学,磁性(キュリー温度)で知られ,放射能分野では妻のマリ・キュリー(Maria Skłodowska-Curie :1867年 ~ 1934年)と共に先駆的研究で知られる。 - キュリー・ワイスの法則(Curie-Weiss law)
強磁性や反強磁性のキュリー点θ以上の温度 T における磁化率χm の振る舞いを説明する法則である。
χm = C/ (T‐θ)
ここで,C はキュリー定数である。
ページの先頭へ