第三部：化学反応　化学反応とエネルギー

　自由エネルギー（ free energy ）
　ある系の化学反応による平衡と自発性の指標で，ヘルマン・フォン・ヘルムホルツが 1882 年に提唱した概念である。
　熱力学的過程の中で，等温等積過程の自由エネルギーをヘルムホルツの自由エネルギー（ Helmholtz free energy ：記号 F ）と呼び，等温等圧過程の自由エネルギーはギブズの自由エネルギー（Gibbs free energy：記号 G ）と呼ばれる。
　なお，IUPAC （国際純正・応用化学連合）では，名称から自由を除いたヘルツホルツエネルギー，ギブズエネルギーとの名称使用を推奨している。また，Gibbs の日本語表記には，分野や時代により，ギブズとギブスの 2種が用いられている。特に，古い文献等ではギブスが多く，最近の文献ではギブズが多い。

　化学反応は，熱力学第二法則（ the second law of thermodynamics ）に従い，系のエントロピー増大，すなわち自由エネルギーが減少する方向に進行し，物質の出入りが無い閉じた系（閉鎖系）の平衡では自由エネルギーが極小値をとる。
　言い換えると，自由エネルギー変化が負であれば化学反応は自発的に起こり，自由エネルギーが極小の一定値を取るとき，系が平衡状態にあることを意味する。

　ギブズエネルギー変化が負で自発的に起きる反応は，発エルゴン反応（ exergonic reaction ）という。逆に，ギブズエネルギー変化が正で自発的に起きない反応は，吸エルゴン反応（ endergonic reaction ）という。
　吸エルゴン反応は，加熱，電気分解，他の発エルゴン反応との組み合わせなど，外部から仕事を与えなければ進行しない反応である。他の発エルゴン反応と組み合わせることを共役という。

　【参考】
　系（ system ）
　考察の対象として，注目する部分を系という。系には，物質とエネルギーの出入りが許される開放系（ open system ），エネルギーの出入りは許されるが，物質の出入りが許されない閉鎖系といわれる閉じた系（ closed system ），及び物質とエネルギーの出入りが許されず，外界から完全に独立した孤立系（ isolated system ）に分けられる。
　熱力学第二法則（ the second law of thermodynamics ）
　エネルギーの移動の方向とエネルギーの質に関する熱力学の基本法則の一つで，様々に表現される。代表的なものに次の 2 つがある。
　エントロピー増大則：断熱系において不可逆変化が生じた場合、その系のエントロピーは増大する。
　クラウジウスの法則：低温の熱源から高温の熱源に正の熱を移す際に，他に何の変化もおこさないようにすることはできない。
　他には，トムソンの法則，ケルビンの法則，クラウジウスの不等式などが第二法則の表現として知られる。
　熱力学では伝統的にはクラウジウスの不等式（Σ( Qi / Ti ) ≦ 0 ）を用いてエントロピーを定義している。
　エントロピー（ entropy ）
　系の微視的な「乱雑さ」を表す物理量という意味付けがなされていた。エントロピーはエネルギーを温度で割った次元（ J/K ）を持ち，記号 S を用いて表される。

　ヘルムホルツの自由エネルギー（ Helmholtz free energy ）
　IUPACでは，名称としてヘルムホルツエネルギー（ Helmholtz energy ）を推奨している。
　等温等積条件の下で，膨張仕事として取り出し可能なエネルギーを表す示量性状態量である。ヘルムホルツエネルギー F は，
　　　　　F ＝ U － T S
　　　　　ここで，U ：内部エネルギー ，T ：熱力学的温度，S ：エントロピーである。
で定義される。

　ギブズ（又はギブス）の自由エネルギー（ Gibbs free energy ）
　IUPACでは，名称としてギブズエネルギー（ Gibbs energy ）を推奨している。
　化学平衡などの等温等圧条件下で，非膨張の仕事として取り出し可能なエネルギーを表す示量性状態量である。ギブズの自由エネルギー G は，
　　　　　G ＝ H － T S
　　　　　ここで，H ：エンタルピー ，T ：熱力学的温度，S ：エントロピー
と定義される。

　等温等圧条件のギブズの自由エネルギー G と等温等積条件のヘルムホルツの自由エネルギー F には，
　　　　　　G ＝ F ＋ ＰV
の関係にある。すなわち，圧力 P ，体積変化 V が系外に為す仕事（ PV ）の分だけ異なる。
　従って，ギブズの自由エネルギー G と内部エネルギー U には，
　　　　　G ＝ U － T S ＋ PV
の関係にある。

　【参考】
　仕事（ work ）
　エネルギーは，“物体や系が持つ仕事をする能力”と定義され，仕事の前後のエネルギー差（ dE ）が仕事 W に相当する。
　物理学においては，力 F を受けた物体が，力の方向に x 移動（変位）した時に，ベクトルの力と変位の積（内積）を，その力のした仕事 W（＝Fx ）という。
　熱力学における仕事は，対象の系と周囲（外界）との間でやり取りするエネルギーである。等温定圧過程（系の温度と圧力が一定での状態変化）で取り出せる仕事は，体積変化を伴う膨張仕事，電気仕事や光仕事などの体積変化を伴わない形態の非膨張仕事に分けられる。
　状態量（ quantity of state ）
　熱力学において，対象とする系（主に平衡状態の物質や場）の状態で一意的に決まる物質量である。状態量は，履歴や経路には依存しない。状態量には，示量性の状態量と示強性の状態量に分けられる。
　示量性（ extensive property ）
　示量性に関する一般的な解説には，「物質量に依存する特性。」，「系全体の量が部分系の量の和に等しくなること。」，「系の大きさ，体積，質量に比例すること。」，「空間内のある 1 点付近における単位体積（あるいは単位面積）当たりの分量を表す物理量のこと。」などがある。
　示量性の状態量の例は，物質量，質量，体積，モル数，化学ポテンシャル，内部エネルギー，エンタルピー，エントロピーなどである。
　「系全体の量が部分系の量の和に等しくなること。」とは，例えば，質量が 1 kg と 1 kg の系を合わせると 2 kg の系になることや，内部エネルギーが 1 J （ジュール）と 1 J の系を合わせると 2 J の系になる（エネルギー保存則）ことを意味する。
　示強性（ intensive property ）
　示強性に関する一般的な解説には，「物質量に依存しない特性。」，「示量性を持たないこと。」，「強さを表す物理量のこと。」，「空間内のある１点における強さを表す物理量のこと。」などがある。
　圧力は，強さを表す物理量で，物質量に依存せず，圧力 1 atm と 1 atm の系を合わせても 2 atm の系にはならない。など示量性を持たない特性（示強性）を示す。
　他に示強性の状態量の例には，温度，密度，濃度，モル体積，モル比熱，速度などがある。

　エントロピー変化と自由エネルギー変化
　熱力学第二法則（ the second law of thermodynamics ）
　等温での状態変化に伴うエントロピー変化ΔS は，その変化を可逆的に行ったときに移動する熱量 Q_rev を熱力学的温度（絶対温度） T で割ったものに等しい。

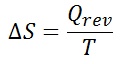
　閉鎖系（closed system）とその周囲（外界）を含む全エントロピー変化（ΔS_全 ）は，それぞれのエントロピー変化の和で表される。
　　　　　　ΔS_全 ＝ ΔS_系 ＋ ΔS_外
　周囲のエントロピー変化（ΔS_外）と系のエントロピー変化（ΔS_系）とには，系の状態変化が可逆的な場合は，ΔS_外 ＝ －ΔS_系の関係にあり，不可逆的な場合は，ΔS_外 ＜ －ΔS_系の関係にある。
　従って，全エントロピー変化は，
　　　　　　ΔS_全 ＝ ΔS_系 ＋ ΔS_外 ≧ 0
となる。ここで，系と周囲との間を可逆的に移動する熱量を Q とすると，ΔS_外 ＝ －Q/ T と表せるので，
　　　　　　ΔS_全 ＝ ΔS_系 － Q/T ≧ 0
とできる。また，等温等圧過程では，Q ＝ΔH_系 とでき，全エントロピー変化の不等式は，
　　　　　　TΔS_全 ＝ TΔS_系 －ΔH_系 ≧ 0
と書き換えることができる。
　ここで，安定化の方向，すなわち不可逆が進む方向（ TΔS_全 が増加する方向）をエネルギーが減少する方向と規定し，自由エネルギー変化をΔG ＝ －TΔS_全 と定義する。
　従って，等温等圧過程での自由エネルギー変化ΔG は，系のエンタルピー変化ΔH とエントロピー変化ΔS を用いて
　　　　　　ΔG ＝ －TΔS_全 ＝ ΔH － TΔS ≦ 0
となる。

　系が周囲にする仕事につて
　W を外界（周囲）が閉鎖系に成した仕事，Q を外界が閉鎖系に与えた熱量としたとき，系の内部エネルギー変化量 ΔU は，
　　　　　　ΔU ＝ Q ＋ W
　等温等圧過程での仕事 W を体積変化による膨張仕事（ －PΔV ）と電気仕事や光仕事などの非膨張仕事（ W_非膨張 ）に分けて表すと，
　　　　　　ΔU ＝ Q － PΔV ＋ W_非膨張
となる。ここで，熱量とエントロピーの関係式，すなわちクラウジウスの不等式（Clausius inequality）　TΔS ≧ Q　を代入すると
　　　　　　ΔU ≦ TΔS － PΔV ＋ W_非膨張
　　　　　　∴　W_非膨張 ≧ ΔU ＋ PΔV － TΔS ＝ ΔH － TΔS ＝ ΔG
の関係が得られる。従って，自由エネルギー変化は，外界が系にした非膨張仕事より小さいことが示される。
　すなわち，系が外界にする非膨張仕事は，逆向きの不等号となるので，自由エネルギー変化以上の仕事を取り出せないこと，言い換えると，自由エネルギー変化量が取り出せる非膨張仕事の最大量になることを示している。

　以上のことからギブズの自由エネルギー変化は，“化学平衡などの等温等圧条件下で，非膨張の仕事として取り出し可能なエネルギーを表す示量性状態量である。”といえる。

　化学平衡（ chemical equilibrium ）
　一般的には，二つの物体を接触させたとき，化学反応による構成成分の変化がなく，物質移動（拡散・溶融・相変化等）がない閉じた系（閉鎖系）での現象をいう。
　可逆反応において正反応の進行速度と逆反応の進行速度とが釣り合って，見かけ上反応が停止した状態の化学平衡では，物体の接触前後の化学ポテンシャルが互いに等しい。

　化学ポテンシャル（ chemical potential ）
　ギブズにより導入された浸透圧や化学反応のようなマクロな物質量の移動が伴う開放系での現象における重要な示強性状態量（ intensive property ）の一つである。
　化学ポテンシャルは，混合物中に存在する一つの成分 1 モル当たり，又は 1 分子当たりの定温・定圧下でのギブズの自由エネルギーを指す。
　言い換えると，ギブズの自由エネルギー（ G ）のある成分 i の偏微分で得られる部分モル量が，ある成分 i の化学ポテンシャル μ_i である。

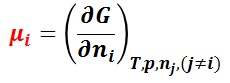
　溶液の成分 A を溶媒とし，その他の成分 i を溶質とする。
　温度 T，圧力 P におけるの純溶媒 A の化学ポテンシャルを μ_A⁰(T,P) としたとき，一般の溶液では溶媒の活量 a_A を用いて，溶媒 A の化学ポテンシャル μ_A は，次のように表現できる。


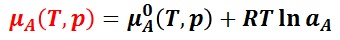
　溶質の混合熱がゼロでなくとも，溶媒についてラウールの法則がおおよそ成立し，溶質についてヘンリーの法則が成り立つ溶液を理想希薄溶液という。
　具体的には，溶媒のモル分率を 1 とみなせるほど溶質の量が極めて少ない希薄溶液は，理想希薄溶液とみなせる場合が多い。
　理想希薄溶液では，溶媒の活量 a_A を溶媒成分のモル分率 χ_A で置き換えることができので，溶媒 A の化学ポテンシャルは，モル分率を用いて次のように表現できる。


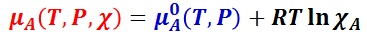
　溶媒 A と溶質 i の種類で決まる温度 T，圧力 P の関数を μ_i^A(T,P) とした時，溶質 i の化学ポテンシャルは次のように表現される。
　

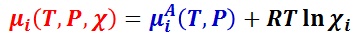
　【参考】
　偏微分（ partial derivative ）
　多変数関数を「特定の変数以外を定数だとみなして」，一つの変数のみに関する微分である。偏微分はベクトル解析や微分幾何学などで用いられる。
　部分モル量（ partial molar quantity ）
　多成分系において，温度，圧力が一定のもとで，そのなかのある一成分を全体の組成がほとんど変化しないような範囲内でさらに添加したとき，その成分 1 mol 当たりのその系の熱力学的状態関数の増加量をいう。たとえば，部分モル体積，部分モルギブズエネルギーなどがある。後者はとくに化学ポテンシャルとよばれる。【化学辞典(第 2版)；森北出版】