第三部:化学反応 化学反応速度
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,化学反応の速度に関連し, 【反応次数と速度定数の関係】, 【反応次数と速度定数の求め方】 に項目を分けて紹介する。
反応次数と速度定数の関係
反応次数(べき乗係数)とは
前節の【反応速度式とは】では,次の化学平衡
αA +βB +γC +・・・ ⇆ ν'α'A' +β'B' +γ'C' +・・・
の反応速度 ν と反応物の濃度との関係は,
ν = k [ A ]α [ B ]β [ C ]γ ・・・
と表すこと,α,β,γをべき乗係数(各物質の反応次数)と呼ぶこと,化学反応式の各成分の係数(化学量論係数)とは概念的に異なることを紹介した。
反応速度式において,べき乗係数の総和( n =α+β+γ+・・・)を全反応次数( overall reaction order )といい,係数 k を n 次反応の速度定数( rate constant )と呼ぶ。
べき乗係数は,理論的に求めることが困難で,実験結果から得られるものである。このため,化学量論係数と異なる場合も少なくない。
さらに,べき乗係数は整数とならない場合,反応条件を変える(多段階反応,触媒の存在など)ことなどによりべき乗係数が変わる場合もある。中には,触媒の作用で,反応物の濃度に依存しない反応もあり,その場合はゼロ( 0次反応)となる。
反応次数(べき乗係数)と化学量論係数が異なる例
例 1 :化学反応に溶媒分子が関わる場合
代表的なもののひとつに,溶媒中で溶媒分子の関わる反応,例えば“ A + H2O → X ”では,化学量論的には 2 次反応と思われるが,反応物 A に比較して溶媒(水の量)が圧倒的に大きいので,水の濃度変化は無視できる。
このため,反応速度式は,A の濃度変化のみに依存するν= k [ A ] で表され,1 次反応の様にふるまう。これを擬 1 次反応ともいう。
例 2 :化学反応が多段階反応の場合
H2 + I2 → 2HI : ν= k [ H2 ] [ I2 ]
水素( H2 )とよう素( I2 )の反応は,化学量論的にも反応速度的にも 2 次反応であるが,同じハロゲン族の分子である臭素( Br2 )との反応は,化学量論的には 2 次反応であるが,反応速度式は,
H2 + Br2 → 2HBr : ν= k [ H2 ] [ Br2 ]1/2 / ( 1 + k’ [ HBr ] / [ Br2 ] )
と複雑な式になる。この要因は,反応が複数の素反応からなる 多段階反応になっているためと考えられる。
ページの先頭へ
反応次数(べき乗係数)と速度定数の求め方
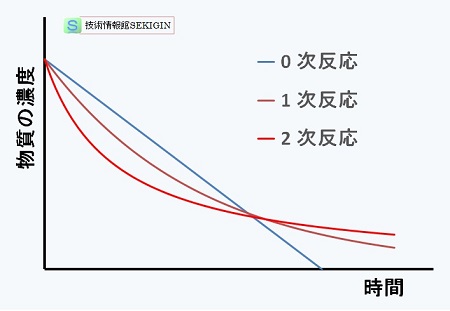
反応次数と濃度変化【模式図】
実験的に直接求められる量は,物質の濃度と時間間隔である。従って,濃度測定の時間間隔や初期濃度を変えることで,種々の時間平均反応速度が得られる。
これらの実験値を用いたべき乗係数の求め方として,代表的な 3 種を次に紹介する。なお,べき乗係数が決まれば,実験で得られた物質濃度変化と時間平均反応速度を反応速度式に代入し,速度定数 k を計算できる。
1)簡便法(濃度プロット)
適当な時間間隔で各反応物の濃度を計測する方法である。
例えば,反応物 A の濃度を C とすると,dC/dt = k[ A0-C ]α と書ける場合を想定する。
この場合は, [ A0-C ]-αdC = -kdt とでき,t = 0 で C = A0 の条件から,積分により
α= 0 の場合: C = -kt + A0
α= 1 の場合: ln C = -kt +ln A0
α= 2 の場合: C-1 = -kt + A0
の関係が得られるので,横軸に時間を採り,縦軸に濃度から得られる次の値をプロットする。
このとき,
濃度 C のプロットで直線が得られた場合はべき乗係数 0 (0次反応),
濃度 ln C のプロットで直線が得られた場合はべき乗係数 1 (1次反応),
濃度 1/C のプロットで直線になった場合はべき乗係数 2 (2次反応)
と判断できる。
2)微分法
反応速度式 ν = k [ A ]α [ B ]β [ C ]γ・・・の両辺の対数をとると,
log10 ν = log10 k +α log10 [ A ] +β log10 [ B ] +γ log10 [ C ]・・・
と変形できる。
短い時間間隔で物質濃度の測定が可能な場合は,複数の濃度別の時間平均反応速度を計測し,各物質の濃度と速度の両対数プロットの傾きから各物質のべき乗係数が求められる。
3)半減期法
反応物 A の初期濃度 A0 の半分の濃度( A0 / 2 )になる期間( t1/2 )を求める。
a )簡便法(測定継続)
濃度測定を継続し,2 × t1/2 の経過時の濃度と初期濃度と関係から求める。
濃度 ほぼ0 :べき乗係数 0 (0次反応)
濃度 A0 / 4 :べき乗係数 1 (1次反応)
濃度 A0 / 3 :べき乗係数 2 (2次反応)
b )初期濃度を変えて測定する方法
初期濃度 A0 の半減期( t1/2 )と異なる初期濃度A'0 での半減期( t'1/2 )を計測し,次式から求める。
α= 1 + ( log10 t1/2 - log10 t'1/2 ) / ( log10 A0 - log10 A'0 )
作図的には,濃度を変えて,横軸に濃度の対数,縦軸に半減期の対数をプロットした場合に,得られた直線の傾きが(α-1 )であることを意味する。
ページの先頭へ