物理 第五部:熱力学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,エネルギー保存則である熱力学第一法則に関し, 【熱力学の基礎】, 【熱力学第一法則とは】, 【定積過程,定圧過程】, 【カルノーサイクル】 に項目を分けて紹介する。
【熱力学の基礎】
熱力学では,巨視的な状態を巨視的な量(圧力,体積,温度などで,状態量という)で記述する。記述に際して,状態量(quantity of state)の間の普遍的な関係(法則)と経験式(状態方程式)とが用いられる。これらの関係を用いることで,少ない状態量(状態変数:state variable , state space)で熱力学的状態を記述できる。
熱力学的状態の記述に用いられる状態量の関数は,例えば内部エネルギー,エントロピー,自由エネルギーなどで,状態関数(state function),熱力学関数(thermodynamic function),熱力学ポテンシャル(thermodynamic potential)と呼ばれる。
なお,熱力学ポテンシャルは,系(system)の熱力学的性質の情報を全て持つように作られた熱力学関数なので,完全な熱力学関数とも呼ばれる。
熱工学などの実用面では,これらの間の関係式を求めることで,熱力学的現象の一般的結論を導き出す手法が用いられる。
系(system)
物理学や化学における系とは,一定の相互作用や相互連関のもとにあるものから成る全体を意味する。W. グライナー,L. ナイゼ,H. シュテッカー著の「熱力学・統計力学」(シュプリンガー・フェアラーク東京,1999)では,熱力学における系について,次のように定義している。
孤立系(isolated system):周囲のものとはいかなる相互作用もしない系をいう。
閉じた系(closed system):周囲とエネルギーのやり取りは許されるが,物質のやり取りがない系をいう。
開放系(open system):周囲とエネルギーおよび物質のやり取りを行なう系をいう。
均一な系(homogeneous system):系のどの部分をとっても性質が同じな系をいう。
不均一な系(heterogeneous system):系の性質がある境界の領域を境に不連続に変化する場合をいう。不均一な系において均一な部分を相(phase), 各相を囲む領域を相境界(phase boundary)という。
状態量(quantity of state , state quantity)
熱平衡にある巨視的な系において,経路に依存せず,熱力学的状態を特徴づける物理量を状態量という。状態量は,直接的に操作できるような量で,通常用いられる状態量には,温度( T ),圧力( P ),体積( V ),物質量( N )などが挙げられる。
独立変数の状態量を熱力学的変数として考えるときには状態変数(state variable , state space)といい,従属変数の状態量は,状態変数の関数となるので,この状態量を状態関数(state function)や熱力学関数(thermodynamic function)という。状態関数を状態変数で表す数式を状態方程式(equation of state)という。
どの状態量を独立変数として選ぶかは任意であり,どの状態量も変数にも関数にもなれるので,一般的には状態変数と状態関数は状態量の同義語としても使われる。
すなわち,状態量(状態変数)は熱平衡状態にある巨視的な系の状態を特徴づける量といえる。
状態量の分類
状態量(状態変数)は,示量性を持つか示強性を持つかにより分類される。
示量状態量(extensive property)
示量変数(extensive variable)ともいわれ,系内の物質の量に比例する状態量をいう。例えば,体積,物質量,質量,エントロピー,エンタルピーがが挙げられる.
示強状態量(intensive property)
示強変数(intensive variable)ともいわれ,物質の量に依存しない状態量をいう。例えば,圧力,温度,密度,濃度,エントロピー,化学ポテンシャルが挙げられる。
状態方程式(equation of state)
状態方程式とは,状態関数を状態変数(状態量)で表す数式(関係式)をいい,巨視的な系の熱力学的性質を反映している。状態方程式の形は,対象とする系により変化する。
具体的な状態方程式は実験的に求められるが,統計力学に基づき,熱力学からは与えられない。
一般的に状態方程式という場合は,流体の圧力を温度,体積と物質量で表す式を指す場合が多いが,固体の弾性体,磁性体,誘電体における状態方程式を考える場合もある。
次には,状態方程式の例として,流体の状態方程式,理想気体の状態方程式を紹介する。
流体の状態方程式
状態量の温度 T ,体積 V ,物質量 N の平衡状態にある流体の圧力 P を適当な関数 f によって
P = f(T , V , N)
のように表した一般式を状態方程式という。
物理学では,変数の記号と関数の記号を混用し,
P = p(T , V , N)
と表すことが多い。
理想気体の状態方程式
熱力学的温度 T ,体積 V ,物質量 n の平衡状態にある理想気体の圧力 P は,気体定数 R を用いて
P = n R T/ V
で与えられる。
この式は,ボイル・シャルルの法則とアボガドロの法則から導かれる。なお,一般的には,分母を払った
P V = n R T
の形で扱われることが多い。
【参考:基礎用語】
- 熱力学的平衡(thermodynamic equilibrium)
熱力学的系が熱的,力学的,化学的に平衡,すなわち,巨視的状態量が一定の値を保つ,変化しない状態をいう。⇒ 熱平衡,力学的平衡,化学平衡 - 熱平衡(thermal equilibrium)
熱の交換が可能な物体系(例えば二つの物体を熱を通す壁を隔てて接触させた系)で,物体間の熱移動がなく相変化もない時に,両物体は熱平衡の状態にあるという。なお,熱平衡にある各物体の温度は等しい。⇒ 熱力学第ゼロ法則 - 力学的平衡(dynamic equilibrium)
二つの物体が釣り合って安定している状態をいう。すなわち,両者の圧力が互いに等しいことなどを意味する。 - 化学平衡(chemical equilibrium)
二つの物体を接触させたとき、化学反応による構成成分の変化や、拡散・溶融・相変化等による物質の移動が生じないとき、両物体は化学平衡 の状態にある(物質移動は物理変化であるが、化学平衡に含めて扱われる)。この場合には、化学変化前後または各独立成分の化学ポテンシャルが互いに等しいことを意味する。 - 独立変数(independent variable)
従属変数を予測するために使われる変数をいう。自由変数(free variable)あるいは不定元(indeterminate)ともいわれる。回帰分析では説明変数(explanatory variable)といわれる。 - 従属変数(dependent variable)
独立変数の変化に応じて変わる数,すなわち予測の対象となる変数をいう。束縛変数(bound variable)ともいわれる。回帰分析では応答変数(response variable , responding variable)や目的変数(target variable)といわれる。
ページの先頭へ
【熱力学第一法則とは】
熱力学の第一法則(first law of thermodynamics)は, 内部エネルギー(internal energy)という概念を導入した熱力学におけるエネルギー保存の法則(law of the conservation of energy)である。
前出の力学的エネルギー保存の法則では,保存力のみが作用する保存力場(conservative force field)での質点の力学的エネルギーが一定となること,すなわち,運動エネルギー K ,位置エネルギー U のとき,力学的エネルギー E は,
K + U = E(一定)
で表されることを紹介した。
熱力学的エネルギー保存の法則である熱力学の第一法則では,系外からの力学的作用,熱的作用,質量作用がない孤立系のエネルギーとして,熱力学的問題に大きく影響しない系全体の運動エネルギー,流体内部の相対的流動に関わる運動エネルギー,外力に対する位置エネルギーを差し引いた系内部の粒子の運動エネルギーと位置エネルギーに対し,内部エネルギーという概念を導入し,熱力学でこの内部エネルギーに対するエネルギー保存則を扱う。
繰り返しになるが,内部エネルギーとは,系の総エネルギーから,系が全体としてもつ運動エネルギー,位置エネルギーを引去った残りのエネルギー,すなわち系内部の状態で決まるエネルギーをいう。具体的には系を構成する分子間の位置エネルギー,分子の並進運動(translational motion)の運動エネルギー,分子の回転・振動によるエネルギーの総和になる。
内部エネルギーは系の状態によって定まる状態量であるが,一般的な物理的,工学的現象では,ある系の状態が変わった場合の変化が問題となる。
孤立系では内部エネルギーは変化しないが,閉じた系又は開放系では,状態の変化で内部エネルギーが変化する。
閉じた系(closed system)
系外から受けた仕事又は系外にした仕事による力学的作用(Mechanical Action),系と系外との熱の出入りに関する熱的作用(Thermal Action)により内部エネルギーが変化する。
状態 1 から状態 2 へ変化するとき,外力が系になす仕事,外界から吸収する熱量の総和が問題となるが,力学的エネルギー保存則と同様に,熱力学第一の法則は,“状態の変化量は,途中の過程によらず,最初と最後の状態によって決まる”と言い換えられる。
例えば,
外部が系に成した仕事 ∂W ,系に与えた熱量 ∂Q としたとき,内部エネルギー変化量 d U は,
d U = ∂Q + ∂ W
で与えられる。
表現を,外部から系に与えた熱量 ∂Q により系が外部にした仕事 ∂W と内部エネルギー変化量 d U の関係は,
∂Q = d U + ∂ W
と表現され,系と外部との関係により正負が変わるので注意しなければならない。
開放系(open system)
閉じた系に加えて,系と系外との物質の出入りに関する質量的作用(mass action)が加わる。すなわち,この系の内部エネルギー変化では,質量的作用として,加えられた質量 m と等価なエネルギー増加分( mc2 :c 光速)を考えなければならない。
実験装置
実験などで,質量的作用のない系を作るためには,考える系を容器で外界と遮断することで可能である。
仕事的作用(力学的仕事,電気的仕事)以外の方法で中の物体に変化を生じないようにするためには,容器の壁を断熱壁で囲むようにすることで可能である。
系の外と仕事以外のやり取りが無く,状態 1 から状態 2 に変化させる過程( d U = ∂W )を断熱過程(adiabatic process)といい,熱力学的な実験では,断熱壁で覆われた容器を用い,できるだけゆっくり(準静的)と変化させることで実現できる。
例えば,カルノーサイクルは,準静的な断熱過程の代表で,この過程は可逆過程である。
ゆっくりとは,系の緩和時間(変化が系全体に均一化されるのに要する時間)より長い時間をかけることで,エントロピー増大を伴わない変化を実現できる。一方,緩和時間より短い時間で変化させると,系の外部のエントロピーが減少し,系の内部のエントロピーが増大する変化が起きる。
ページの先頭へ
【定積過程,定圧過程】
仕事(work)とは,力 F を受けた物体が,力の方向に x 移動(変位)した時に,力と変位の積(内積)をいう。
W = Fx
一方,静止流体の圧力(静圧)は,設定した面に対して法線方向の垂直応力(normal stress)のみが働き,法線方向のせん断力は働かない。
圧力や張力などの垂直応力は,力に垂直な面の単位面積当たりの力と定義されるので,断面積 A ,力 F のとき,圧力 p は
p = F/ A
で表される。
従って,外部の圧力 p の場合に,系が外部に対してする仕事 𝜕 W は,
𝜕 W = PAx =p dV
となり,圧力( P )と体積増加分( Ax = dV )との積で表される。
このことは,体積変化が無ければ,どのような圧力であっても仕事をしない( 𝜕 W = 0 )ことを意味する。
静圧を受ける系の静的な変化に対し,系に与えた熱量 𝜕 Q ,内部エネルギー変化量 dU ,系がした仕事 𝜕 W ,に関する熱力学第一法則の式は,
𝜕 Q = dU + 𝜕 W = dU + p dV
と書ける。
定積過程(isochoric process)
系の体積を一定に保ちながら,系の状態を変化させる熱力学過程で,等容変化ともいわれる。すなわち,体積一定(dV = 0)なので,熱力学第一法則の式は,
𝜕 Q = dU
と,系の変化で出入りした熱量に等しい分だけ内部エネルギーが変化する。すなわち,定積過程では,どのような経路を経ても熱が保存される。
エンタルピーの変化(d H)に関しては,体積一定(dV = 0)なので,
d H = d ( U + pV ) = d U + p dV +V dp = dU+ V dp
と書ける。
定圧過程(isobaric process)
流体の系の圧力を一定に保ちながら,系の状態を変化させる準静的な熱力学過程である。この場合は,体積変化を伴うので,系が仕事をする( W ≠ 0 )ので,熱力学第一法則の式は,
𝜕 Q = dU + 𝜕 W = dU + p dV
と書ける。
エンタルピーの変化(d H)に関しては,圧力一定(dp = 0)なので,
d H = d ( U + pV ) = d U + p dV +V dp = dU + p dV = 𝜕 Q
と書ける。エンタルピーは,系の状態のみで決まる量(状態量)なので,圧力一定の時は,系に入る熱量は系の状態のみに依存し,変化経路によらず一定(⇒ヘスの法則)であることを示す。
ヘスの法則(Hess' law)
ヘスの法則とは,熱力学第一法則が確立する以前に,ロシアの化学者ジェルマン・アンリ・ヘス(1802 ~ 1850 年)が化学反応(熱化学反応)に関して提唱した法則で,総熱量不変の法則( the law of constant heat summation )ともいわれる。
ヘスの法則は,「化学反応での反応熱は,反応前後の状態のみで決まり,反応経路によらず一定である」や「化学反応のエンタルピー変化は,反応経路によらず一定」と表現される。
ページの先頭へ
【カルノーサイクル】
カルノーサイクル(Carnot's cycle)とは,フランスの物理学者ニコラ・レオナール・サディ・カルノー(1796 ~1832 年)が,熱機関(蒸気機関)の熱効率について行った思考実験で,熱効率が最大になる理想的な可逆サイクルをいう。
カルノーサイクルは,温度の異なる2つの熱源の間で動作する可逆熱サイクルの一種で,蒸気などが高温と低温との間を断熱圧縮→等温(吸熱)膨張→断熱膨張→等温(放熱)圧縮の 4 行程(準静的過程)で循環する。なお,断熱変化,等温変化に関しては別途紹介する。
蒸気の熱エネルギーを機械エネルギーに変換する機関(蒸気機関,汽力発電など)の熱サイクルは,T-S 線図,P-V 線図を用いて説明されるのが一般的である。
T-S 線図とは,熱力学(的)温度( T )を縦軸,熱量の変化エントロピー( S )を横軸にしたグラフで,P-V 線図とは,蒸気の圧力( P )を縦軸,蒸気の体積( V )を横軸にしたグラフである。
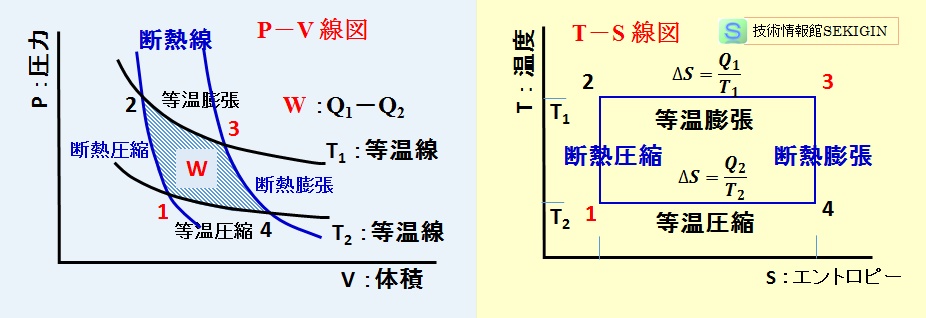
カルノーサイクルの P-V 線図,T-s 線図
熱力学の第一法則よりカルノーサイクルの理論熱効率ηth は,
で与えられ,理論熱効率を超える熱効率の機関が存在しないことが示される。
ここで,T2 = 0 K(絶対零度)のとき,熱効率 1 となるので,理論上では第二種永久機関と成りうるが,実用上では,絶対零度に達することが不可能なことや熱力学第二法則(エントロピー増大則)により,第二種永久機関の実現は不可能である。
なお,カルノーサイクルのエントロピー変化量は,
で与えられ,T – S 図に示すように,全行程を経ると,エントロピー変化量は差し引きゼロになる。
ページの先頭へ