第三部:化学反応 酸・塩基反応
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,酸・塩基反応を利用した化学分析法(中和滴定)の基本を, 【弱酸を強塩基で滴定】, 【滴定曲線】, 【当量点の pH 】 に項目を分けて紹介する。
弱酸を強塩基で滴定
完全に電離している強酸と異なり,弱酸の電離平衡では,水溶液中に未電離の分子が多数存在する。その程度は弱酸の種類と濃度により大きく異なる。
そのため,当量点での pH 変化が明瞭なものから不明瞭なものまで様々である。
1価の弱酸を 1価の強塩基で滴定(イオン濃度と pH変化)
ここでは, 1 価の弱酸(酢酸など)の試験液を 1 価の強塩基(水酸化ナトリウムなど)の水溶液で滴定する場合を考える。
水溶液の pH は,【弱酸・弱塩基の pH 】で紹介したように,電解平衡,水の自己解離定数,物質収支,電気的中性原理から求めることができる。
① 電離平衡
1 価の強塩基は,解離定数が著しく大きいので,完全に電離しているものと仮定できる。
強塩基の水溶液 : YOH + 2H2O → Y+ (aq) + OH-
一方,1 価の弱酸は,次の電離平衡を考慮しなければならない。
弱酸の水溶液 : HX + 2H2O ⇆ X- (aq) + H3O+
Ka = [ X- ] [ H3O+ ] /[ HX ] 式 1)
② 水の自己解離定
2H2O ⇆ H3O+ + OH-
KW = [ H3O+ ] [ OH- ] = 1.0×10-14 式 2)
③ 物質収支
試験液中の酸のモル濃度 CA は,滴定操作による試験液容量の変化を考慮しなければならない。そこで,滴定前の酸の初期モル濃度 CA0 (知りたい値),容量 VA とし,塩基水溶液(滴定剤)の添加した容量を VB とすると,試験液中の酸のモル濃度は,
酸の全量 : CA = [ HX ] + [ X- ] = CA0 VA /( VA + VB ) 式 3)
となる。
一方,強塩基はすべてイオン化するので,試験液中の塩基イオンのモル濃度 [ Y+ ] は,滴定に用いる溶液(滴定剤)の初期モル濃度を CB0(既知濃度)とすると,
[ Y+ ] = CB0 VB /( VA + VB ) 式 4)
となる。
④ 電気的中性原理
[ H3O+ ] + [ Y+ ] = [ X- ] + [ OH- ] 式 5)
⑤ 添加剤の量と pH の関係
式 1)と式 3)から
Ka = [ X- ] [ H3O+ ] / [ HX ] = [ X- ] [ H3O+ ] /( CA - [ X- ] )
∴ [ X- ] = Ka CA / ( [ H3O+ ] + Ka ) 式 6)
式 2)と式 5)から
KW = [ H3O+ ] [ OH- ]
= [ H3O+ ] ・〔 [ H3O+ ] + [ Y+ ] - [ X- ] 〕 式 7)
式6)と式 7)を用いて [ H3O+ ] に関してまとめると
[ H3O+ ]3 + [ H3O+ ]2 ( Ka + [ Y+ ] ) + [ H3O+ ] ( Ka [ Y+ ] - Ka CA - KW ) - Ka KW = 0
となり,pH は,三次方程式の正の実数根から求められるが,この解を求めるのは容易ではないので,次の 2つの仮定(当量点より酸性側,塩性側)から二次方程式に変換して求める。
仮定 1(酸性側)
当量点より酸性側では,イオン積 KW ( 10-14 ) は,他の項に比較し著しく小さいので,無視( 0と置く)できる。そこで,
[ H3O+ ]2 + [ H3O+ ] ( Ka + [ Y+ ] ) + Ka ( [ Y+ ] – CA ) ≒ 0
と近似でき,この二次方程式の正の解は,
[ H3O+ ] = { -( Ka + [ Y+ ] ) + [ ( Ka + [ Y+ ] ) 2 – 4 Ka ( [ Y+ ] – CA ) ] 1/2 } /2
となる。
仮定 2(塩基性側)
当量点より塩基性側では,ヒドロニウムイオンの量が小さいので,[ H3O+ ] 3 の項を無視できるとする。そこで,式は
[ H3O+ ] 2 ( Ka + [ Y+ ] ) + [ H3O+ ] ( Ka [ Y+ ] – Ka CA – KW ) – Ka KW ≒ 0
と近似でき,この二次方程式の正の解は,
[ H3O+ ] = { -( Ka [ Y+ ] – Ka CA – KW ) + [ ( Ka [ Y+ ] – Ka CA – KW ) 2 + 4 ( Ka + [ Y+ ] ) Ka KW ] 1/2 } /2( Ka + [ Y+ ] )
となる。
従って,pH ( = - log10 [ H3O+ ] ) は,滴定剤の陽イオン濃度([ Y+ ] )の関数として得られる。
ページの先頭へ
滴定曲線(弱酸・強塩基滴定)
濃度 CA0 ,CB0 ,及び容量 VA は,滴定操作を進めても変化しない値である。一方,滴定操作で変化する値は,VB となる。
従って,横軸に添加した強塩基の容量 ( VB ) ,縦軸に溶液の pH をとると,下図の弱酸の試料を強塩基で滴定した曲線(滴定曲線)が得られる。
下図の滴定曲線は,0.1 mol/L の酢酸( Ka = 1.75×10-5 )水溶液を強塩基水溶液で滴定した場合を想定し,酸性側の推定式と塩基性側の推定式から得られた値を示す。
滴定が進み,当量点 [ Y- ] = CA に近づくと pH の急激な変化が起こるが,前節で紹介した【強酸の強塩基による滴定】に比較して,当量点付近の変化は緩慢で,終点の判定が難しいことが想定される。
当量点における滴定剤の添加量( VB )と塩基のモル濃度( CB0 )から,未知の酸の初期モル濃度を,
CA0 VA /( VA + VB ) = CB0 VB /( VA + VB )
∴ CA0 = CB0 VB /VA
から求められる。
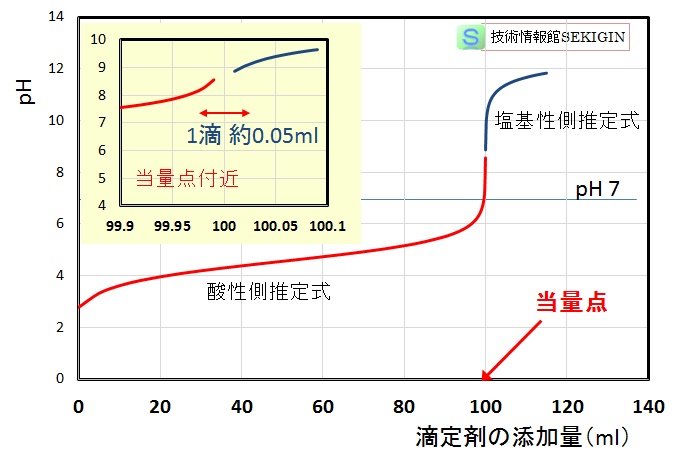
滴定曲線: 酢酸 Ka = 1.75×10-5
弱酸水溶液( 0.1 mol /L ,100ml )を強塩基(0.1 mol / L)水溶液で滴定
ページの先頭へ
当量点の pH
0.1 mol /L の酢酸( Ka = 1.75×10-5 )水溶液を強塩基水溶液で滴定した場合の当量点( CA )付近の pH を上記の近似式で計算すると,酸性側の近似式では 0.9999 CAで pH 8.54 ,塩基性側の 1.0001 CA で pH 8.87 と計算された。
当量点 pH の簡便な求め方
滴定に強塩基として水酸化ナトリウムを用いた場合に,当量点の水溶液は,酢酸ナトリウムを水に 0.1 mol /L となるように溶解した場合と同じと考えることができる。
すなわち,水溶液中では,
CH3COONa (aq) → CH3COO- (aq) + Na+ (aq)
CH3COO- (aq) + H2O ⇆ CH3COOH (aq) + OH-
K = [ CH3COOH (aq) ] [ OH- ] / [ CH3COO- (aq) ]
の反応が想定される。
ここで,電離定数 K の分母と分子にヒドロニウムイオン( [ H3O+ ] )を掛ける。
次いで,酢酸の酸解離定数 Ka = [ CH3COO- ] [ H3O+ ] / [CH3COOH (aq) ] の関係と水のイオン積 KW = [ H3O+ ] [ OH- ] の関係を用いると,
K = [CH3COOH (aq) ] [ OH- ] [ H3O+ ] /( [CH3COO- ] [ H3O+ ] )
= [ OH- ] [ H3O+ ] ・( [CH3COOH (aq) ]/( [CH3COO- ] [ H3O+ ] )
∴ K= KW・( Ka-1 ) 式 1)
の関係が得られる。
一方で,電気的中性の条件
[ H3O+ ] + [ Na+ ] = [ CH3COOー ] + [ OH- ]
に物質収支の関係
[ Na+ ] = [ CH3COO- ] + [CH3COOH (aq) ]
を代入することで,
[ H3O+ ] + [ CH3COO- ] + [ CH3COOH (aq) ] = [ CH3COO- ] + [ OH- ]
∴ [CH3COOH (aq) ] = [ OH- ] - [ H3O+ ]
が得られる。
ここで,0.1mol/L 酢酸水溶液中のイオンの関係, [ Na+ ] ≫ [ H3O+ ] を考慮すると,[ OH- ] ≫ [ H3O+ ] と仮定できる。従って,上式は,
[ CH3COOH (aq) ] ≒ [ OH- ] 式 2)
と近似できる。
さらに,Ka = 1.75×10-5 なので [ CH3COO- ] ≫ [CH3COOH (aq) ] すなわち,
[ CH3COO- ] ≒ CA 式 3)
と近似できる。
以上の近似をまとめ,式1)に式 2),3)を代入する。
KW /Ka = K = [ CH3COOH (aq) ] [ OH- ] /[ CH3COO- ]
≒ [ OH- ] 2 /CA
∴ [ OH- ] ≒ ( CA KW /Ka ) 1/2
の関係が得られる。従って,酢酸水溶液( CA = 0.1mol/L )の当量点の pH は,
pH = -log10[ H3O+ ] = -log10( KW /[ OH- ]) ≒ -log10{( KW Ka /CA )1/2}
= ( pKW + pKa + log10 CA ) /2 = ( 14 + 4.56 - 1 ) /2 = 8.78
が得られる。
ページの先頭へ