物理 第五部：熱力学

　熱力学第一法則で紹介したように，熱力学で扱う過程には，前提とする条件の違いや定義の違いで，断熱過程（adiabatic process），等温過程（isothermal process），定積過程（isochoric process），定圧過程（isobaric process），準静的過程（quasistatic process），可逆過程（reversible process），不可逆過程（irreversible process）などが知られる。
　
　断熱過程（adiabatic process）
　断熱変化（adiabatic change）ともいわれ，外部との熱の出入りなしに行われる物体の状態変化の過程で，断熱圧縮と断熱膨張の過程がある。
　気体の場合は，断熱圧縮では外部からされた仕事により温度が上がり，断熱膨張では気体が外部にした仕事だけ内部エネルギーが減って温度が下がる。
　詳細を後述するが，理想気体が準静的な断熱変化を行う場合，ポアソンの法則が成り立つ。理想気体の準静的な断熱変化は可逆過程のためエントロピーは一定である。
　一般には，断熱変化を可逆的に行えばエントロピーは変わらないが，不可逆的に行えば，熱力学第二法則で紹介するように，エントロピーは減少することなく増大する。
　
　等温過程（isothermal process）
　等温変化（isothermal change）とも呼ばれ，熱の出入りは許すが，系をある状態から別の状態へと変化させる等温過程の前後で，系の温度は変化しない。
　詳細を後述するが，理想気体では系の内部エネルギーも変化せず，準静的な等温過程ではボイルの法則 （ pv＝一定）が成り立つ。
　
　定積過程（isochoric process）
　系の体積を一定に保ちながら，系の状態を変化させる熱力学過程で，等容変化ともいわれる。すなわち，体積一定（dV = 0）なので，熱力学第一法則の式は，
　　　　　　　𝜕 Q = dU
と，系の変化で出入りした熱量に等しい分だけ内部エネルギーが変化する。すなわち，定積過程では，どのような経路を経ても熱が保存される。
　
　定圧過程（isobaric process）
　流体の系の圧力を一定に保ちながら，系の状態を変化させる準静的な熱力学過程である。この場合は，体積変化を伴うので，系が仕事をする（ W ≠ 0 ）ので，熱力学第一法則の式は，
　　　　　　　𝜕 Q = dU + 𝜕 W = dU + p dV
と書ける。
　エンタルピーの変化に関しては，圧力一定（dp = 0）なので，
　　　　　　　d H ＝ d (U ＋ pV ) = dU ＋ p dV ＋V dp = dU＋ p dV = 𝜕 Q
と書ける。エンタルピーは，系の状態のみで決まる量（状態量）なので，圧力一定の時は，系に入る熱量は系の状態のみに依存し，変化経路によらず一定（⇒ヘスの法則）であることを示す。
　
　準静的過程（quasistatic process）
　系がある状態から別の状態へ移る場合に，途中のどの状態も熱力学的平衡の状態から極めてわずかしかずれないようにして，ゆっくり変化する過程をいう。
　準静的過程は，理論的には無限の時間をかけて変化ことを想定した熱力学上の理想的な概念である。しかし，実用上では変化の速度が十分に遅ければ準静的過程とみなされる。一般的には，変化に要する時間が緩和時間（relaxation time）より長い場合に準静的過程とみなされる。
　準静的過程では，同じ条件のもとで変化を逆行させることができるので，準静的過程は可逆過程である。しかし，可逆過程は必ずしも準静的過程ではない。
　
　可逆過程（reversible process）
　ある系が状態 A から状態 B へ移った時，系以外の外界に変化を生ずる。なんらかの過程を用いて再び状態 A へ戻す。このときに外界になんの変化も残さず戻せた（外界も元の状態に戻る）場合に，状態 A から状態 B への変化を可逆変化（reversible change）といい，用いた過程を可逆過程という。
　可逆過程は，状態変化がない平衡状態でのみ生じる過程であるため，厳密には，可逆過程は理想化されたもので存在し得ない。
　しかしながら，準静的過程を用いることで，状態の可逆的な変化を想定することが出来る。
　
　不可逆過程（irreversible process）
　ある系が状態 A から状態 B に移った時，系以外の外界に変化を生ずる。この系を再び状態 A に戻した時，外界が元の状態に戻らない変化を不可逆変化（irreversible change）や非可逆変化といい，この過程を不可逆過程という。
　日常生活で目にするほと んど全ての過程は，膨張や摩擦を伴う不可逆過程であ る。
　
　【参考：基礎用語】

• 緩和時間（relaxation time）
  　外的条件の変化で，系が新しい状態に移行するまでの時間。熱力学的には，系が非平衡から平衡に変化するまでに要する時間（目安）。
• 断熱圧縮（adiabatic compression）
  　外部との熱の出入りなしに気体を圧縮すること。外部からの仕事で温度が上がる。
• 断熱膨張（adiabatic expansion）
  　気体が外部との熱のやりとりなしに膨張すること，外部に仕事をして温度が下がる。
• 理想気体の特性
  　比熱比：γ= C_p/ C_V ，定積モル比熱： C_V = R/ (γ– 1 ) ，定圧モル比熱： C_p = γR/ (γ– 1 ) ，内部エネルギー：U = U₀ + C_V ( T – T₀ )，エンタルピー： H = H₀ + C_p ( T – T₀ )

　 断熱過程では，系の外部との熱の出入りがないので，熱力学第一法則の式は，系に与えた熱量 𝜕 Q = 0 となり，内部エネルギー変化量 dU ，系がした仕事 𝜕 W ，の関係は，
　　　　　　　dU ＝ – 𝜕 W
となる。
　すなわち，断熱過程では，系が外部に仕事をすると内部エネルギーが減少（断熱膨張）し，逆に外部から系に仕事をすると内部エネルギーが増加（断熱圧縮）する。
　一般的には，断熱圧縮で温度が上昇し，断熱膨張で温度が低下する。ただし，真空中に気体を拡散する場合など，外部の圧力がゼロの場合は，膨張しても仕事をしないので，断熱自由膨張（adiabatic free expansion）と呼ばれ，内部エネルギー，温度の変化が無い。
　
　準静的断熱過程（quasistatic adiabatic process）
　別途紹介したカルノーサイクルが代表的な準静的断熱過程である。
　準静的断熱過程は，外部と仕事のやりとりのみが存在する可逆の過程である。
　可逆過程ではエントロピー（ S ）と熱量（ Q ），熱力学(的)温度（ T ）の間に
　　　　　　
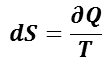
の関係がある。断熱過程では，外部と系の熱の出入りが無いので 𝜕Q = 0 ，すなわち，dS = 0 となるので，準静的断熱過程は，エントロピーが変化しない過程で，等エントロピー過程ともいわれる。
　
　仕事
　理想気体が準静的断熱過程で変化するとき，圧力と体積の間にはポアソンの法則が成り立つので，理想気体の比熱比をγ，適当な定数を C₁ とした時，ポアソンの法則は，
　　　　　　
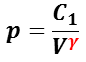
とできる。
　系の状態 A から状態 B への準静的断熱過程の全仕事量 W_{A – B} は，体積 V_{A – B} から V_{A – B} までの仕事（ 𝜕 W = p dV ）>の積分なので，
　　　　　　
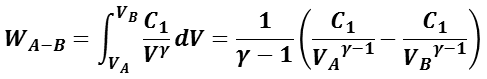
となる。ここで，ポアソンの法則の定数 C₁ は，系の状態 A から状態 B とも同一なので，
　　　　　　
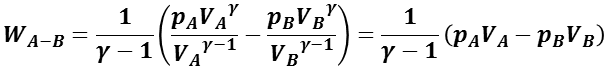
とできる。ここで，理想気体の状態方程式（ pV = nRT ）を用いると，
　　　　　　
となり，内部エネルギーの変化に等しい。

　ポアソンの法則（Poisson's law）とは，理想気体が準静的な断熱変化を行う場合の圧力 P と体積 V の次の関係をいう。
　　　　　　　pV^γ = 一定
　ここで，指数のγは比熱比で与えられる。
　
　前述したように，理想気体の準静的断熱過程で，系が外部にした仕事 pdV とすると，
　　　　　　　dU ＝ – 𝜕 W = – pdV
とできる。
　1 モルの気体分子は，温度 T で 1 自由度につき RT/ 2 （ R ：気体定数）の内部エネルギーを持つので，気体分子の自由度 f と内部エネルギー U の関係は，
　　　　　　　U = f×RT/ 2
となる。従って，
　　　　　　　dU ＝ (f / 2)×R dT = – pdV
と変形できる。ここで理想気体 1 モルの状態方程式（ pV = RT ）とから，
　　　　　　　(f / 2)×dT/ T = – dV/ V
が得られる。この両辺を積分すると，
　　　　　　　(f / 2)× ln (T/ T₀) = – ln (V/ V₀)
となるので，整理すると，
　　　　　　　
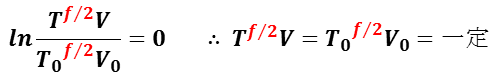
とできる。理想気体分子の自由度 f と比熱比γの関係（ γ＝ ( f＋2 )/ f ）から，
　　　　　　　TV^{γ – 1} = 一定
と変形できる。
　理想気体の状態方程式を用いると，ポアソンの法則として知られる
　　　　　　　pV^γ = 一定
に変形できる。
　
　【参考：基礎用語】

• 自由度（degree of freedom）
  　一般には，変数のうち独立に選べるものの数をいう。物理的には，ある運動状態や平衡状態を表すのに必要な任意に独立に変化させることができるものの数をいう。
  　分子種の自由度と比熱比
  　気体分子の自由度の観点からは，He , Ar などの単原子分子，N₂ , O₂ などの 2 原子分子，CO₂ , NH₃ , CH₄ などの多原子分子に分けられる。
  　単原子分子
  　自由度 f ＝ 3 （並進），γ≒ 5/ 3（1.67）
  　2 原子分子
  　自由度 f ＝ 4（並進 3 ＋回転2 ），γ≒ 7/ 5（1.40）
  　多原子分子
  　 f＝ 6（並進 3 ＋回転 3 ），γ≒ 4/ 3（1.33）

　等温過程（isothermal process）とは，等温変化（isothermal change）とも呼ばれ，系の温度が常に一定であることを意味するのではなく，熱の出入りは許すが，等温過程の初めと終わりの温度が同一となる過程である。
　理想気体では系の内部エネルギーも変化せず，準静的な等温変化ではボイルの法則 （ pV ＝一定）が成り立つ。
　
　温度一定の環境下で，系が平衡状態の遷移で外部に行う仕事には上限が存在する。このため，ヘルマン・ルートヴィヒ・フェルディナント・フォン・ヘルムホルツ（1821 ～ 1894年）が，静力学における位置エネルギー（ポテンシャルエネルギー）と同様な形で，熱力学における状態量として，自由エネルギー（free energy）を導入した。
　
　静力学とは，建築物，構造物，機械などの部材で，静的状態（時間で系の要素の相対的な位置が変化しない状態）に働く力やトルクなどを扱う分野をいう。
　
　自由エネルギーは，等温等積過程の記号 F で表されるヘルムホルツの自由エネルギー（Helmholtz free energy），等温等圧過程の記号 G で表されるギブズの自由エネルギー（Gibbs free energy）に大別される。
　なお，ヘルムホルツの自由エネルギー F とギブズの自由エネルギー G との間には，その定義により，系の体積変化がする仕事 pV だけ異なる
　　　　　　　G = F + pV
の関係にある。
　
　ヘルムホルツの自由エネルギー
　内部エネルギー U ，温度 T ，エントロピー S とすると，
　　　　　　　F ＝ U－TS
　で定義される。圧力 p ，体積 V とすると，微分形の関係式は dF＝－SdT－pdV である。
　ヘルムホルツの自由エネルギーは，系の持つ内部エネルギーのうち仕事として外部に取り出せるエネルギーの最大値といわれる。
　
　ギブズの自由エネルギー
　内部エネルギー U ，温度 T ，エントロピー S ，圧力 p ，体積 V とすると，
　　　　　　　G ＝ U－TS＋pV
　あるいは，
　　　　　　　G = F + pV
で定義される。微分形の関係式は dG ＝－SdT＋Vdp である。
　ギブズの自由エネルギーは，系の持つエンタルピー（ H ＝ U ＋ pV）のうち仕事として外部に取り出せるエネルギーの最大値といわれる。
　
　ヘルムホルツ（Hermann Ludwig Ferdinand von Helmholtz）
　ヘルマン・ルートヴィヒ・フェルディナント・フォン・ヘルムホルツ（1821年～1894年）は，ドイツ出身の生理学者，物理学者。1847年に論文『力の保存について』を発表。マイヤー，ジュール，ケルビン卿と並ぶエネルギー保存則（熱力学の第一法則）確立者の一人。ヘルムホルツ方程式，ヘルムホルツの自由エネルギー，ケルビン・ヘルムホルツ不安定性，ギブズ-ヘルムホルツの式などで知られる。
　
　ギブズ（Josiah Willard Gibbs）
　ジョサイア・ウィラード・ギブズ（1839年～1903年）は，アメリカの数学者，物理学者，物理化学者。熱力学ポテンシャル，化学ポテンシャル概念を導入。相平衡理論，相律の発見など今日の化学熱力学の基礎を築く。ベクトル解析の創始，ギブズの自由エネルギー，ギブズ-デュエムの式，ギブズ-ヘルムホルツの式などで知られる。

　物質量 n の理想気体を等温過程（絶対温度 T ）で，状態 A から状態 B に移行した場合のヘルムホルツの自由エネルギーの変化（Δ F ）を考える。
　
　理想気体の状態方程式（ pV = nRT ： 物質量 n モル，気体定数 R ）を用いると圧力 p は， 温度 T ，体積 V の関数として，
　　　　　　　
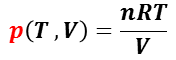
で与えられる。
　
　等温過程（ dT = 0 ）のヘルムホルツの自由エネルギーの変化（Δ F ）は，
　　　　　　　
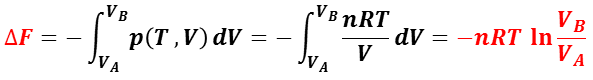
となる。
　
　等温可逆過程では，系が外部になす仕事はヘルムホルツの自由エネルギーの減少量に等しく（ W = ΔF ），理想気体では系の内部エネルギーも変化しない（Δ U = 0 ）。
　従って，系が外部から得る熱 Q は，
　　　　　　　
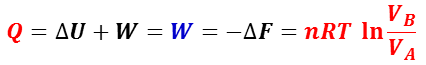
となる。
　なお，等温自由膨張では W = 0 なので，Q = W = 0 である。