物理 第五部:熱力学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,熱力学第二法則に関し, 【熱力学第二法則とは】, 【可逆変化と不可逆変化】, 【クラウジウスの法則】, 【ケルビンの法則(トムソンの法則)】, 【エントロピーとは】, 【熱伝導】, 【断熱自由膨張】 に項目を分けて紹介する。
【熱力学第二法則とは】
熱力学では,物体の熱力学的状態を,状態量(圧力,体積,温度など)の関数である熱力学特性関数(内部エネルギー,エントロピー,自由エネルギーなど)で表し,それらの間の関係式を求めることで,現象の一般的結論を導き出す手法が用いられる。
熱力学の基本原理は,熱力学第ゼロ法則(熱平衡の概念),熱力学第一法則(エネルギー保存),熱力学第二法則(エントロピー増大),熱力学第三法則(絶対零度に関するネルンスト・プランクの仮説)などの経験則で構成される。
熱力学第二法則(second law of thermodynamics)
エントロピー増大の法則(law of entropy increase)ともいわれ,エネルギーの移動の方向とエネルギーの質に関する経験則で,歴史的に様々に表現されてきたが,その内容はほぼ同じである。
例えば
● 巨視的にみると,動的な現象は不可逆である。
● 熱化学サイクルを一巡したときに,他に効果をいっさい残さずに,熱を低温熱源から高温熱源へ移動させることはできない(クラウジウスの法則)。クラウジウスの不等式などの表現がある。
● 一つの熱源から正の熱を受け取り,これを全て仕事に変える以外に,他に何の変化もおこさないようにするサイクルは存在しない(ケルビンの法則,トムソンの法則)
● 断熱系において不可逆変化が生じた場合,その系のエントロピーは増大する(エントロピー増大則)。
ページの先頭へ
【可逆変化と不可逆変化】
可逆変化(reversible change)
振り子の運動など,力学的エネルギーにおいて保存力(conservative force)のみが作用する保存力場(conservative force field)では力学的エネルギー保存の法則が成立する。
このため,周期的運動(振動)で紹介したように,状態 A から状態 B への変化に対し, 他に影響を与えずに状態 B から状態 A に戻ることができる。
熱力学でも同様に,物質系がある状態 A から他の状態 B に変化した時,再びもとの状態 A に戻る(同じ経路の必要はない)ときに外界に対して何の変化も残さない時,状態 A から B の変化を可逆変化という。可逆過程は,実用面での利用目的より,理論的考察のために理想化された過程である。
不可逆変化(irreversible change)
実環境での振り子は,支点の摩擦,空気抵抗などの保存力ではない力が作用する。この場合は,減衰振動で紹介したように,外力を加えるなどの影響なしには,状態 B から状態 A に戻ることができない。
熱力学でも同様に,物質系がある状態 A から他の状態 B に変化した時,物質系のみならず外界の変化もなく,元の状態に戻す過程が存在しないとき,状態 A から状態 B の変化を不可逆変化という。不可逆変化は非可逆変化ともいわれる。
物質を構成する分子や原子の運動は,可逆的な法則で支配されているにもかかわらず,巨視的な物質での摩擦現象,や後述の熱伝導,気体の真空膨張(自由膨張)などは,感覚的にも明らかな不可逆変化と考えられる。
この不可逆性を微視的な運動から明確に証明するのは困難(不可逆性問題)である。
熱力学第二法則は,熱力学第一法則では説明困難な巨視的な物質の不可逆過程をエントロピー増大の概念を用いて扱っている。
【参考:基礎用語】
- 保存力(conservative force)
物体が力 F の作用を受け,ある点から別の点に移動する時に,力 F のする仕事 W が経路によらず位置 r だけで決まる場合の力 F を保存力という。
この場合に,位置 r での位置エネルギーを V(r) とした時,保存力 F = – ∇V(r) で与えられる。
重力,ばねの復元力,クーロン力などの保存力のみが働く場(保存力場)では,力学的エネルギー保存則(law of the conservation of energy)が成り立つので,この力を保存力と呼ぶようになったといわれている。 - 振動(oscillation , vibration)
物体の位置,電流の強さなどの物理量が一定時間(周期)ごとに一定の(減衰振動などではほぼ一定の)値をとるよう,規則正しく変動することをいう。
振動系はその構造によって定まった固有振動をもつ。振動系に復元力だけが働くときには自由振動(free vibration),抵抗などのように振幅を減少させる制動力も働くときには減衰振動(damped vibration)が起る。周期的な強制力が加わると強制振動(forced vibration)が起り,強制力と固有振動との振動数が一致すれば共振(共鳴,resonance)が生じる。 - 摩擦(friction)
物体が他の物体の表面に接しながら運動しようとするとき,接触面に沿って相対運動を妨げる力(摩擦力)がはたらく現象をいう。物体が相対的に静止している場合の静止摩擦,運動を行っている場合の動摩擦に分けられる。
ページの先頭へ
【クラウジウスの法則】
クラウジウスの法則(Clausius statement)は,クラウジウスの原理(Clausius theorem)ともいわれ,ドイツの物理学者ルドルフ・ユリウス・エマヌエル・クラウジウス(1822 ~ 1888年)の提案した法則で,次のように表現される。
“低温の熱源から高温の熱源に正の熱を移す以外に,他に何の痕跡も残さないようにすることはできない”,
“高温の熱源から低温の熱源に正の熱が移る現象は不可逆である”
クラウジウスは,氷と水の共存している 0 ℃の低熱源と水と水蒸気の共存している 100 ℃の高熱源の間で,準静的断熱過程の代表で可逆過程のカルノーサイクル(Carnot's cycle)が働く装置を考え,高熱源から熱を取り出し,低熱源に熱を移し,カルノーサイクル自身ももとに戻る過程が可能であることは示された。
次いで,低熱源から熱を取り,高熱源に熱を移す過程(例えばエアコン)で,カルノーサイクル自身が元に戻り,なんの影響も残さないようにすることを試みたが,いずれの試みも失敗した。
これらの試みの結論として,このような装置はないとの結論に至り,上述のクラウジウスの法則にまとめた。
クラウジウスの不等式(Clausius inequality)
仕事から熱 Q が発生した時,熱力学的温度 T との比 Q/ T (熱効率)とした時,カルノーサイクルなどの可逆過程では,
![]()
が成り立つ。
すなわち,可逆過程で高熱源 T1 に接している状態から低熱源 T2 に接している状態に変化しても,Q/ T は不変となる。クラウジウスが,これをエントロピーと命名した。
可逆過程の全過程では,
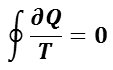
が成立するが,不可逆過程を考慮した場合として,
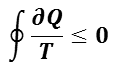
を提案している。これをクラウジウスの不等式という。
記号 ⨕ は,閉曲線の場合の線積分(curvilinear integral)を示す。
線積分とは,曲線積分ともいい,空間内のある領域において関数が連続で,またその領域においてなめらかな曲線が与えられているとき,これを曲線に沿う関数の積分をいう。
クラウジウス(Rudolf Julius Emmanuel Clausius)
ルドルフ・ユリウス・エマヌエル・クラウジウス(1822年~1888年)は,ドイツの物理学者。熱力学第一法則・第二法則の定式化,エントロピーの概念の導入など、熱力学の基礎を築く。
ページの先頭へ
【ケルビンの法則(トムソンの法則)】
ケルビンの法則(Kelvin statement,Kelvin's expression of second law of thermodynamics)は,日本では一般的にトムソンの法則ともいわれ,一般的には,ケルビン卿として知られるイギリスの物理学者初代ケルヴィン男爵ウィリアム・トムソン(1824 ~ 1907 年)が,同時代のクラウジウスとは独立して発見した熱力学の原理で,次のように表現される。
“一つの熱源から熱をとり,外に対して正の仕事をするサイクルを行う装置は存在しない”
他に,“一つの熱源から正の熱を受け取り,これを全て仕事に変える以外に,他に何の変化もおこさないようにするサイクルは存在しない”や,“一つの熱源から熱を吸収するだけで,それをすべて仕事に変換することは不可能である”などとも表現される。
ここで,ケルビンの法則(トムソンの法則)が正しくないと仮定する。すなわち,ケルビンの法則で否定されている装置(一つの熱源から熱をとり,外に対して正の仕事をするサイクルを行う装置)を仮定することになる。
仮定した装置には,1 サイクルの間に,一つの高熱源から熱 Q をとり,外に対して正の仕事 W(= Q )をする装置 1 があり,この仕事 W を使い,高熱源より温度の低い他の低熱源との間にある理想気体のカルノーサイクルを逆に運転する装置 2 がある。
カルノーサイクルでは,低熱源から正の熱 Q1 を取り,高熱源に熱 Q2 を移す。装置 2 では,熱力学第一法則より,
Q2 = W + Q1
が成立する。
装置 1 +装置 2 の全体装置としては,低熱源から正の熱 Q1 を取る。
高熱源では,仕事 W をするための熱 Q をとる行程があるので,
Q2 – Q = W + Q1 – Q = Q1
が与えられ,系の他に何の影響も残さないように働くことになる。
以上から,仮定した装置は,クラウジウスの法則“低温の熱源から高温の熱源に正の熱を移す以外に,他に何の痕跡も残さないようにすることはできない”に反することになり,ケルビンの法則が正しくないという仮説は否定される。
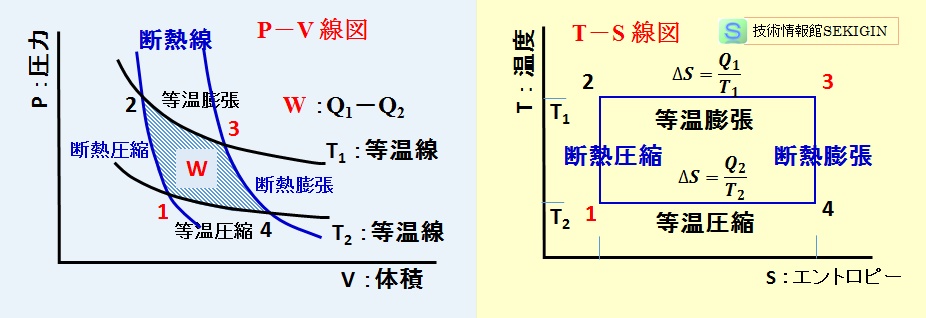
カルノーサイクルの P-V 線図,T-s 線図
- カルノーサイクル(Carnot's cycle)
フランスの物理学者ニコラ・レオナール・サディ・カルノー(1796 ~1832 年)が,熱機関(蒸気機関)の熱効率について行った思考実験で,熱効率が最大になる理想的な可逆サイクルをいう。
カルノーサイクルは,温度の異なる2つの熱源の間で動作する可逆熱サイクルの一種で,蒸気などが高温と低温との間を断熱圧縮→等温(吸熱)膨張→断熱膨張→等温(放熱)圧縮の4行程(準静的過程)で循環する。 - ケルヴィン(William Thomson, 1st Baron Kelvin OM)
初代ケルヴィン男爵 ウィリアム・トムソン(1824年~1907年)は,イギリスの物理学者。爵位に由来するケルビン卿(Lord Kelvin)の名で知られる。絶対温度(熱力学(的)温度,ケルビン)の導入,クラウジウスとは別に熱力学第二法則(トムソンの原理,ケルヴィンの原理)の発見,ジュール=トムソン効果の発見,ケルビンの渦定理など,古典的な熱力学の開拓者の一人。ケルビンやトムソンとも呼ばれる。
ページの先頭へ
【エントロピーとは】
熱力学におけるエントロピー(entropy)は,系の微視的な「乱雑さ」を表す指標として,前述のクラウジウスの不等式(Clausius inequality)を用いて定義される。エントロピーは,エネルギーを温度で割った次元( J・K– 1 )をもつ。
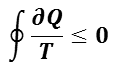
可逆過程のエントロピー
クラウジウスの法則(Clausius theorem)で,可逆過程の全過程(閉じた状態変化のサイクル)は,可逆的な過程の「状態 A →状態 B →状態 C 」と「状態 C →状態 D →状態 A 」に分けることができるので,

が成立する。なお,全過程が可逆なのでクラウジウスの不等式は等号となる。
すなわち,始まりと終わりの状態が同じ場合には,途中の経路の状態が異なってもエントロピーは不変である。
ここで,可逆過程の状態 A から状態 B のエントロピーを S (A-B) ,可逆過程状態 A から状態 C でのエントロピーを S (A,C) とした時,エントロピーの差 S (A,C) - S (A,B) は,可逆過程の状態 A から状態 B を経由して状態 C に至ると考えることができるので,
S (A,C) - S (A,B) = S (A,B) +S (B,C) - S (A,B) = S (B,C)
となる。
このことは,基準とする状態(状態 O )のエントロピー値が不明でも状態 A と状態 C のエントロピー差(ΔS)は求められることを意味する。
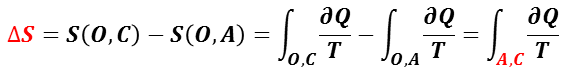
準静的可逆過程の微小な変化は,両辺を微分して,
![]()
で与えられる。なお,断熱過程(∂Q = 0 )では dS = 0 である。
従って,準静的な定圧過程の熱力学第一法則から,
![]()
が成立する。
不可逆過程を含めたエントロピー
状態 A から状態 C へと移る不可逆過程を含む任意の過程( A,C )と,状態 C から状態 D を経由して状態 A へ移る可逆過程( C,D,A )のサイクルを考える。
このとき,可逆過程のエントロピーは,S(C,D,A) = – S(A,D,C) とできるので,サイクル全体では,不可逆過程を含むので,クラウジウスの不等式を用いて次のようになる。
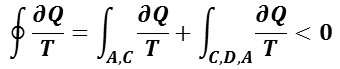
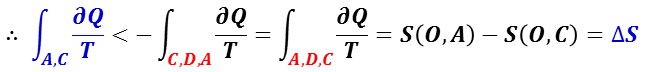
となり,不可逆過程を含む状態変化の微小変化については,
![]()
と書け,断熱過程(∂Q = 0 )では dS > 0 となる。
すなわち,可逆な断熱過程は,エントロピー変化がゼロの等エントロピー過程であるが,不可逆過程を含む断熱過程では,正のエントロピー変化を有する。
従って,不可逆過程を含む状態変化ではエントロピーが増加するため,熱エネルギーのすべてを他のエネルギーに変換することはできない。
これが,熱力学第二法則,すなわちエントロピー増大の法則(law of entropy increase)である。
ページの先頭へ
【熱伝導】
ここで,簡単のため,2 つの物体( A ,B )の定積熱容量 CV が等しく,それぞれの温度が TA < TB とする。
物体 A と B を接触させ,熱平衡に達したときに温度 Tf になった場合を考える。
ここで,エントロピー変化を見るため,直接接触の過程は複雑なので,それぞれの物体を隔離して別々に準静的に変化させ,温度 Tf になってから接触させる過程を考える。
準静的過程でのエントロピーの微小変化 dS =∂Q/ T ,定積過程の熱力学第一法則(∂Q = dU ),定積熱容量( CV = dU/ dT ) とからエントロピーの変化量ΔS は,
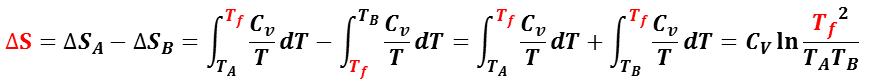
で与えられる,
一方,熱平衡に至る過程で物体 A に入った熱量と物体 B から出た熱量が同じなので,
![]()
となる。
ここで,TB = TA +α,α > 0 ,とすると,
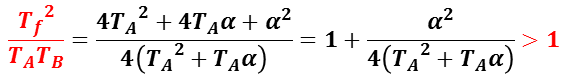
とできる。
すなわち,エントロピー差 ΔS > 0 となり,物体の接触による熱伝導過程は不可逆といえる。
ページの先頭へ
【断熱自由膨張】
断熱膨張(adiabatic expansion)とは,断熱変化の一つで,熱の出入りなしに体積を増大する現象である。外部へ仕事をする場合は,内部エネルギーの減少,気体の温度の低下が起きる。
自由膨張(free expansion)とは,気体を真空中に噴出させて膨張させた場合など,外部に対して仕事をせずに膨張することをいう。
断熱自由膨張は,熱の出入りなしで,外部に仕事をしないで膨張する現象で,温度の変化が無いので,等温自由膨張ともいわれる。
体積 V の理想気体が真空に向かっていっきに体積 V’まで膨張する場合,途中の温度を定義するのが困難であるが,変化の前後の温度が同じである。
そこで,連続に変化する準静的等温膨張を考える。
エントロピーの微小変化 dS と理想気体 1 モルの熱量変化∂Q は,熱力学第一法則,定積熱容量( CV = dU/ dT),理想気体の状態方程式( pV = nRT )から,
![]()
と書ける。
断熱自由膨張では,初めと終わりの温度が同じ( dT = 0 )で体積が増大( V’/ V > 1 )するので,
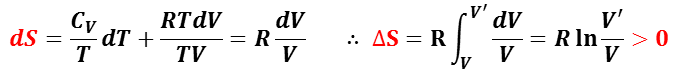
となり,エントロピー差 ΔS > 0 から断熱自由膨張は不可逆といえる。
ページの先頭へ