第三部:化学反応 化学反応速度
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,化学反応の開始と速度に影響する要因に関連して, 【反応開始とは】, 【活性化とは】 に項目を分けて紹介する。
反応開始とは
日常の生活に用いている都市ガス(天然ガス)は,メタン( CH4 )がその主成分( 90 %程度)である。メタンが空気中で燃焼する際の熱化学方程式は,
CH4 (g) + 2O2 (g) → CO2 (g) + 2H2O (g) ⊿CH0 = -890.71 kJ/mol
又は
CH4 (g) + 2O2 (g) = CO2 (g) + 2H2O (g) + 890.71 kJ
で表される。反応式から,メタンの燃焼は発熱反応で,メタン 1 mol当の燃焼により 890.71 kJ のエネルギーを取り出せることが分かる。
【熱化学方程式】では,発熱反応は,自発的に進む反応と紹介した。
実際には,室温で都市ガスを空気と混合しただけでは反応せず,ガスと空気の混合物に,種火や放電火花などの火源を近づけなければ着火しないことを日常で経験している。
このことは,室温でこの化学反応(発熱反応)を開始するためには,瞬間的に高温状態となる点火源などの引き金( trigger )が必要であることを意味する。
メタンの燃焼反応の引き金を考察するために,可燃物の引火点,燃焼点,発火点(着火点)について整理する。
引火点( flash point )
火源が無くなると反応が進まない温度をいう。
燃焼点( fire point )
引火点より数℃程度高い温度で,火源がなくなっても燃焼が継続できる最低温度である。消防法の危険物の分類では,引火後に 5 秒間燃焼が継続する最低の温度をいう。
発火点( ignition point )
空気中で,火源がなくとも化学反応が開始する最低温度である。自然発火温度,着火温度ともいわれる。
すなわち,着火のための火源とは,メタンと空気の混合物の一部を発火点以上の温度するための装置と考えられる。
なお,発熱反応により,十分な反応熱が得られる場合には,周辺のガスを燃焼点以上の温度に維持できるため,火源を遠ざけても燃焼が継続される。
しかし,発熱反応の反応熱が小さい場合には,火源を遠ざけると,放熱が発熱に勝り,燃焼点以上の温度を維持できないため,ついに周囲の温度が引火点を下回ることで燃焼反応が停止する。
参考
メタン( CH4 )
モル質量 16.042 g /mol ,融点 – 182.5 ℃,沸点 – 161.6 ℃,引火点 - 188 ℃(代表例),発火点 537 ℃(代表例),
ページの先頭へ
【活性化とは】
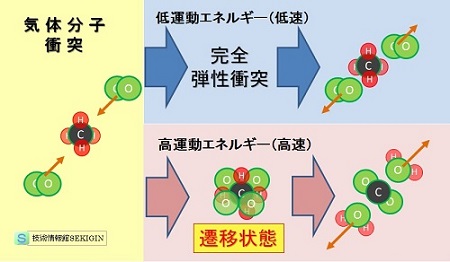
分子衝突時のエネルギーと衝突後の挙動【模式図】
簡単・分り易さのため3分子同時衝突の図にしたが,実際には時間差を持つ複雑な挙動である。
気体分子は,【気体分子の熱運動】で紹介したように,互いの衝突(完全弾性衝突)で運動エネルギーを交換しながら,与えられた温度(内部エネルギー)に応じた速度分布を持つ。
発火点以下の温度では,分子が衝突しても完全弾性衝突となり,互いのエネルギーを交換するだけで分子構造に変化はない。
しかし,気体の温度上昇(内部エネルギーの増加)により,上昇温度に比例して気体分子の持つ運動エネルギーが増加する。
分子の運動エネルギーがある値を超えると,下図に示すように,分子同士の衝突で分子間の斥力を超えて互いに接近する。これにより,衝突した複数の分子で構成される遷移状態( transition state )を経て化学反応が起きると考えられる。
分子の持つエネルギー分布
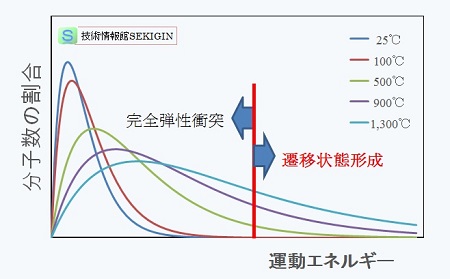
ある分子のエネルギー分布と衝突後の挙動【模式図】
気体の温度を上げてゆくと,【気体分子の熱運動】で紹介したように,与えられた温度での分子の速度分布が変わる。
分子の持つ並進運動のエネルギーは,その速度の二乗に比例するので,下図には,マクスウェルの分布を参考に,温度を変えた時の分子の運動エネルギーと分子数の割合の関係を模式的に示した。
温度の上昇と共に,高い運動エネルギーを持つ分子の数が増えることが分かる。遷移状態を形成できる最少の運動エネルギーが存在し,そのエネルギーを超える運動エネルギーを有する分子が反応継続に必要な数だけ出現する温度を発火点と考えることができる。
遷移状態とは
化学反応で反応物から生成物に変わる過程で通る最もエネルギーの高い状態を遷移状態という。遷移状態では,衝突した分子の力学的エネルギー(運動エネルギー)が分子内部のエネルギーに変換され,元の構造と異なるゆがんだ構造となる。この状態になった分子を活性錯体,活性複合体,活性錯合体などとも呼ぶ。
遷移状態は,直接観察できる反応中間体とは異なり,新たな結合の形成過程で直接観測することができない状態と考えられている。
【参考】
マクスウェル分布( Maxwell distribution )
熱力学的平衡状態で気体分子の速度が従う分布関数(マクスウェル-ボルツマン分布:Maxwell - Boltzmann distribution ともいう)である。
ここで,分子の質量 m ,ボルツマン定数 k ,温度(ケルビン) T とすると,分子速度νの分布は,次の分布式で表せる。
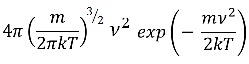
マクスウェル速度分布式
衝突( collision )
運動している 2 つの物体が接触し,短時間に力を相互に及ぼし合う物理的現象をいう。 2 つの物体が衝突した時,衝突前の一方の物体の相対速度をνとすると,衝突後の相対速度ν’は,ν’= - e νとなる。
e は反発係数と呼ばれ,0 から 1 の間の値を取る。e = 1 であれば運動エネルギーが保存されるので,完全弾性衝突( perfectly elastic collision )といわれる。完全弾性衝突以外は,運動エネルギーの一部が熱エネルギーなどに変換される。
ページの先頭へ