第三部:化学反応 化学反応速度
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,化学反応の速度に関連し, 【速度定数と活性化エネルギー】, 【活性化エネルギー(アレニウスプロット)】, 【速度定数の温度依存性】, に項目を分けて紹介する。
速度定数と活性化エネルギー
ここでは活性化エネルギーと反応速度の関係を簡潔に紹介する。
化学反応は,活性化エネルギーを超える運動エネルギーを持つ分子(粒子)の衝突で生じる。すなわち,
反応速度 ∝ 「分子の衝突頻度」×「活性化エネルギーを超える分子の割合」
と定義できる。
分子の衝突頻度
気体分子運動論によると,分子 A と B の衝突頻度 ZAB は,
ZAB = nA nB πρAB ( 8kBT /πμ)1/2
ここに,nA, nB :単位体積に含まれる分子の数
ρAB :衝突半径
T :熱力学的温度
kB :ボルツマン定数
μ:分子の速度
で表される。すなわち,衝突頻度は,分子 A,B の分子の数 n(濃度)の積に比例する。
活性化エネルギーを超える分子の割合
活性化エネルギーを超える分子の割合は,1 mol 当たりの活性化エネルギー( Ea ),気体定数( R )と熱力学的温度( T )を用いて
exp ( -Ea / RT )
で与えられる。この関数はボルツマン因子と呼ばれる。
式から,活性化エネルギーを超える分子の割合は,活性化エネルギーの指数に逆比例することが分かる。
参考
ボルツマン因子( Boltzmann factor )
温度 T の熱平衡状態の系で,特定の状態が発現する相対的な確率を定める重み因子をいう。
Z :分配関数,kB :ボルツマン定数(=気体定数 / アボガドロ数),T :熱力学的温度のとき,エネルギー Ei の状態が出現する確率は
Z-1 exp ( - Ei /kBT )
で表せる。指数関数の項をボルツマン因子と呼ぶ。
ページの先頭へ
活性化エネルギー(アレニウスプロット)
アレニウスの式( Arrhenius equation )とは,1884年にスウェーデンのスヴァンテ・アレニウスが提唱した化学反応の速度を予測する式である。このため,活性化エネルギーはアレニウスパラメータとも呼ばれる。
アレニウスの式: k = A exp ( -Ea / RT )
ここに,k :速度定数
A :頻度因子
Ea :活性化エネルギー
R :気体定数(≒ 8.314 J K-1 mol-1 )
T :熱力学的温度
指数関数部分は,前述のボルツマン因子である。
速度定数は,アレニウスの式で示されるように 1 mol 当たりの活性化エネルギーと温度に依存する。
アレニウスの式の対数をとると,
ln k = ln A - Ea / RT = - ( Ea / R ) ( 1/T ) + ln A
となる。
すなわち,横軸に熱力学的温度の逆数( 1/T ),縦軸に速度定数の対数( ln k )をとり作図(アレニウスプロット)すると,図のような直線が得られる。この直線の傾き( Ea /R )から当該化学反応の活性化エネルギーを求めることができる。
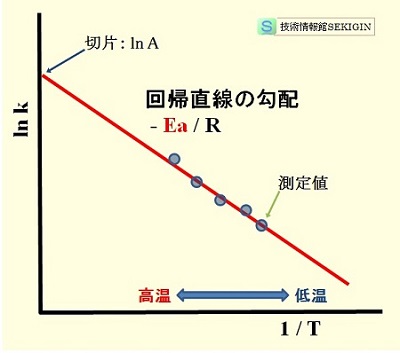
アレニウスプロットとは【模式図】
前項で紹介した速度定数を求める実験を,温度を変えて複数回( 4 回以上)実施する。
化学反応の種類によっては,下図に示すように,ある温度で反応経路が変わり,折れ線になるなど,必ずしも単調な直線にならない反応もあるので,できるだけ広い温度範囲で複数回実験するのが望ましい。
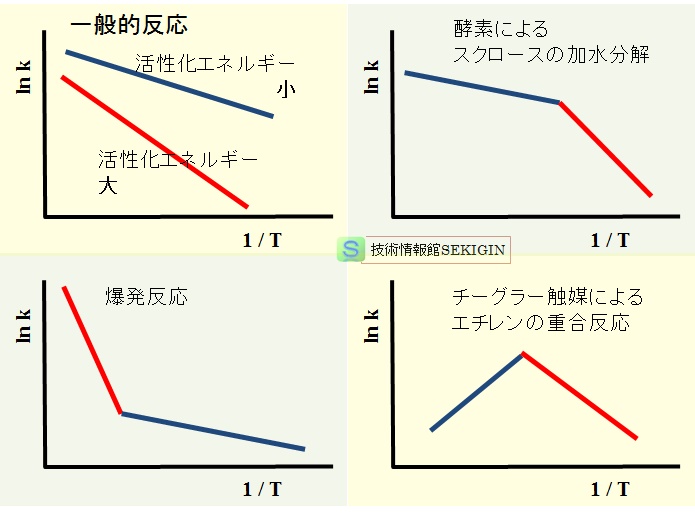
アレニウスプロットにみる化学反応のタイプ【模式図】
参考図:化学便覧
ページの先頭へ
速度定数の温度依存性
一般的に,化学反応は,温度が 10 ℃上がると反応速度は 2 ~ 3 倍上昇すると説明される。これは,室温付近で容易に進む身近な反応に対する目安であり,厳密には活性化エネルギーから計算するのが望ましい。
反応速度,すなわち速度定数の温度依存は,アレニウスの式{ k = A exp ( -Ea /RT ) }で評価できる。
温度を 20 ℃→ 30℃に変えた時,速度定数が 2 倍になる活性化エネルギーを求めると, Ea ≒ 51.2 kJ mol-1 となる。3 倍になるには, Ea ≒ 81.2 kJ mol-1 のときである。
活性化エネルギーの大きい反応の例
ヨウ化水素( HI )の分解反応( 2HI → H2 + I2 )の活性化エネルギーは,Ea = 174 kJ mol-1 (白金触媒下では 49 kJ mol-1 )である。この値を用いて,アレニウスの式で無理やり計算すると,20 ℃→ 30℃の温度上昇で速度定数は約 10.5 倍になる。本当か!?
実際は,ヨウ化水素の分解反応の活性化エネルギーが大きいので,室温に放置したのでは反応が進まない。反応開始には加熱( 400 ℃以上)が必要で,反応開始温度付近( 400 ℃→ 410℃)で計算すると,速度定数は 10 ℃の温度上昇で約 1.6 倍となる。
ページの先頭へ