第三部:化学反応 電極反応
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,電気化学での起電力・電気量に関連し, 【電極の電位と起電力】, 【ボルタ電池で何が起きている】, 【電気量】 に項目を分けて紹介する。
電極の電位と起電力
電極間の電位分布
電池内部の電極間の電位分布を模式的に示すと,下図のように,電極表面極近傍の電解液に形成する電気二重層( charge double-layer )内で電位が変化し,電解液の沖合では電位変化はほとんどないと考えてよい。
電気二重層内の電位は,酸化反応,又は還元反応での物質濃度の変化に起因する電位変化,すなわち電極電位と考えられる。
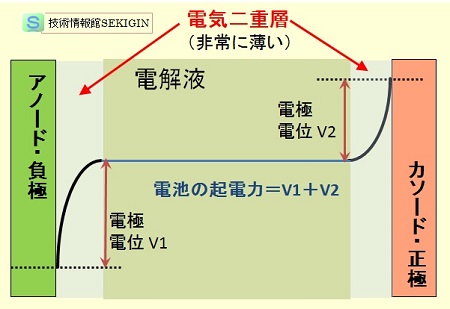
電極間の電位分布【模式図】
起電力( electromotive force , EMF )とは,電流を生じさせる電位の差(電圧)である。
化学反応による電池の起電力は,標準電極電位から理論的な起電力を,式量電位と過電圧からはより実用的な起電力が計算できる。
【電池】では,電池別の起電力を紹介したが,その起電力について詳しく見てみる。
電池の理論起電力は,電池図の左の電位(アノード,負極)と右の電位(カソード,正極)とを合わせたものであるが,右の半反応は酸化反応であるため,標準電極電位,又は式量電位の決まり(還元反応で表す)から,電位の符号は逆の符合になる。従って,電池の起電力は,電極電位の絶対値
電池の理論起電力=|(左・アノードの電極電位)-(右・カソードの電極電位)|
で表される。
次表には,代表的な電池の半反応と電極電位( V vs. SHE )をまとめて示す。なお,各電池の起電力(理論値:実測値)は,ボルタ電池( 0.7626 V : 1.1 → 0.4 V ),ダニエル電池( 1.10 V : 1.1 V ),鉛蓄電池( 1.81 V : 約 2 V ),水素燃料蓄電池( 1.23 V : 1.2 V )である。
| 電池名 | 電池図 | 負極(左) | 電位 | 正極(右) | 電位 |
|---|---|---|---|---|---|
| ボルタ電池 | Zn | H2SO4(aq) | Cu | Zn → Zn2+ + 2e- | - 0.7626 | 2H+ + 2e- → H2 | 0.0000 |
| ダニエル電池 | Zn | ZnSO4(aq) || CuSO4(aq) | Cu | Zn → Zn2+ + 2e- | - 0.7626 | Cu2+ + 2e- → Cu | 0.340 |
| 鉛蓄電池 | Pb | H2SO4(aq) | PbO2 | Pb → Pb2+ + 2e- | - 0.1263 | PbO2 + 4H+ + SO42- + 2e- → PbSO4 + 2H2O |
1.685 |
| 水素燃料電池 | Pt・ H2 | KOH | O2 ・Pt | 2H2 → 4H+ + 4e- | 0.0000 | O2 + 4H+ + 4e- → 2H2O | 1.229 |
【参考】
電気二重層( electric double layer )
組成が異なる二つの相の接触界面で,一方の側に余分の正電荷が,他方の側に余分の負電荷が分布する層。( JIS K 0213 )
式量電位( formal potential )
ネルンスト式において,活量の代わりにモル濃度を用いてネルンスト式と同じ形式で表して定義したときの値( E0' )。 電極反応 O+ne ⇄ R において,電気活性物質 O,R のモル濃度をそれぞれ CO,CRとし,気体定数を R,ファラデー定数を F,絶対温度を T とすれば,平衡電位 E は次の式で表す。
E = E0' + ( RT/nF ) ln ( CO / CR )
この値は活量係数に関する項を含むので,溶液のイオン強度によって変化する。見かけの電位ともいう。( JIS K 0213 )
ネルンストの式( Nernst equation )
酸化還元反応: ox + ze- ⇆ red
が平衡状態の時,基準電極(標準水素電極)との電位差 E (平衡電極電位)は,
E = E0 + ( RT /zF ) ln ([ox] /[red] )
の関係にある。
ここで,E0 :標準電極電位,R :気体定数( 8.314 JK-1mol-1 ),T :熱力学的温度( K ),
z :酸化還元反応にて授受される電子数,F :ファラデー定数( 96,485 C mol-1 ),ln :自然対数,
[ox] :酸化型の化合物の活量,[red] :還元型の化合物の活量である。
なお,25℃の時は,RT /F = 0.0592 となる。
ページの先頭へ
ボルタ電池で何が起きている
電解液(希硫酸水溶液)に導線で結ばれた亜鉛板と銅板を浸漬して形成されるボルタ電池の実測起電力は,電極の電解液浸漬直後に 1.1V を示し,時間と共に低下し,最終的には 0.4V 程度で安定する。
この測定結果は,次に示す電池の電極電位から求まる理論起電力 0.7626V とは大きく異なる。
ボルタ電池の電池図: Zn | H2SO4(aq) | Cu
アノード反応: Zn → Zn2+ + 2e- 電極電位: -0.7626 V(vs.SHE)
カソード反応: 2H+ + 2e- → H2 電極電位: 0.0000 V(vs.SHE)
電池の理論起電力=|(-0.7626) - (0.000) |= 0.7626 (vs.SHE)
実際の電池で測定された起電力と理論起電力の違いは,硫酸に浸漬する直前の銅板表面が酸化銅で覆われていること,浸漬後の水素イオンの還元反応で水素過電圧の影響を受けることによるものと考えられる。
銅板(カソード)表面の影響
ボルタ電池構成直前のカソード電極の銅表面は,大気中で構成された酸化銅の被膜で覆われていると考えられる。
電極を希硫酸に浸漬した直後を観察すると,水素の発生が見られず,銅板表面の変色(綺麗になる)ことが経験される。
すなわち,酸化した銅表面で,酸化銅( CuO )などの還元反応が生じていると考えられる。
カソード反応: CuO + 2H+ + 2e- → Cu + H2O 電極電位: 0.340 V(vs.SHE)
電池の理論起電力=|(-0.7626) - (0.340) |= 1.10 (vs.SHE)
水素過電圧の影響
しばらくして,銅板表面の酸化銅が消費されると,起電力が低下し,水素イオンの還元反応に移行する。しかし,銅板表面で水素の還元反応を始めるための活性化エネルギーが比較的大きく,反応を継続するためには,このエネルギーに相当する電圧が必要となる。これに相当する電圧を水素過電圧という。
水素過電圧は,電極にもちいる材料,電極表面の性状,電解液の組成の影響を受けるが,ボルタ電池の銅電極の水素過電圧は 0.3 V程度となる。このため,電池の起電力は理論起電力の 0.76V から 0.4V 程度まで低下した。
【参考】
中性の水や常温の空気中の銅表面
酸素,水,二酸化炭素,環境汚染因子などと反応し,生成した黒色の酸化銅(Ⅱ)( CuO ),青緑色の緑青( 塩基性炭酸銅 CuCO3・Cu(OH)2 ,塩基性塩化銅 CuCl2・Cu(OH)2 ,塩基性硫酸銅 CuSO4・Cu(OH)2 など)の比較的厚い層で表面が覆われる。
過電圧( overpotential , overvoltage )
単一電極において,ある値の電流が流れているときのその電極の電位と平衡電位との差。
作用電極に電流 i が流れているとき,その電極の電位を E( I ) とすれば,過電圧 E( I ) = E( 0 ) – I R で表す。
ここに,E( 0 ) : I = 0 のときの E( I ) の値,R :溶液の抵抗( JIS K 0213 )
水素過電圧( hydrogen overvoltage )
過電圧には,反応物質の活性化に余計なエネルギーが消費されるための活性化過電圧( activation overpotential , activation overvoltage ),電極表面と溶液内部の濃度が異なるために生じる濃度過電圧( concentration overpotential , concentration overvoltage ),電極表面での抵抗から生じる抵抗過電圧が複合的に作用している。
水素発生反応に対しては,水素過電圧と称している。例えば,主な金属の硫酸( 0.5 mol/L )中の水素過電圧は,Pt ( 0.005 V ) ,Au ( 0.02 V ) ,Fe ( 0.08 V ) ,Ag ( 0.15 V ) ,Ni ( 0.21 V ) , Cu ( 0.23 V ) ,Pb ( 0.64 V ) ,Zn ( 0.7 V ) ,Hg ( 0.78 V ) などである。電気めっきなどの場合に重要な情報である。
ページの先頭へ
電気量
電荷(electric charge)は,素粒子(elementary particle)の持つ性質の一つである。電荷の量を電気量(quantity of electricity)や電荷量(quantity of electric charge , charge quantity)という。
単位時間当たりにある面を通過する電気量は,電流(electric current)と定義される。従って,電気量=電流×時間と定義される。
電流の国際単位系の単位( SI 単位)は,基本単位 アンペア(A)と定義されているので,電気量(電荷量)の単位は,電流(A)×時間(s)=クーロン(C), SI 組み立て単位 C = A・s となる。
電気量と物質変化量
電気分解の電気量と分解量,電気めっきの付着量と電気量,電池の放電容量と電極での反応量は,酸化還元反応による物質変化量と電気エネルギーとの関係から求められる。
電気量と物質変化量の関係は,1833 年にイギリスの科学者マイケル・ファラデーによって発見された次の 2つの物理法則,すなわちファラデーの電気分解の法則( Faraday's laws of electrolysis )で説明される。
第一法則
電極で反応したり,生成したりするイオンや物質の量(物質量)は,電解液中を通過した「電気量」に比例する。
電極で反応・生成する物質量 n ( mol ) ,流れた電気量 Q ( C ) =電流 I ( A ) ×時間 t ( s ) ,比例定数 K としたとき,第一法則は次式で表せる。
n = K・I・t = K・Q
第二法則
同じ電気量によって反応したり,生成したりするイオンの物質量は,そのイオンの「価数」に反比例する。
電極で反応・生成する物質量 n ( mol ) ,流れた電気量 Q ( C ) ,比例定数 K’ ,イオンの価数 z としたとき,第二法則は次式で表せる。
n = ( K'/z )・Q
ここで,物質量 1mol の 1価のイオンを反応させる電気量を F と定めると,比例定数は K = K'/z = 1/(zF) とできる。この物質量 1mol 当たりの電気量 F をファラデー定数 ( 9.6485 × 104 C/mol ) とする。
物質の分子量 M ( g/mol )としたとき ,ファラデーの電気分解の法則により,電気量 Q( C )で反応する物質の質量 m( g )は,
n = m/M = Q/( zF ) ∴ m = Q・M/( zF )
ここに,z :イオン価数,F :ファラデー定数 ( 9.6485 × 104 C/mol )
とできる。すなわち,反応する物質の量は,流れた「電気量」と物質の「電気化学当量」に比例する。
備考
物質の化学反応の量的関係を表す当量( equivalent )とは
化学当量( chemical equivalent )=分子量/価数= M/z
電気化学当量( electrochemical equivalent )=化学当量/ファラデー定数 = M/(zF)
【蛇足】:電池の容量については,電気量(C=As)ではなく,一般的には電池内の反応物質を 1時間で使い切ってしまう場合を想定した容量( Ah や mAh )で表示され,放電容量と称される。なお,俗語で電流量と称している例もみられる。
ページの先頭へ