第二部：物質の状態と変化　気体の圧力

　気体は，粒子（分子，原子）間の距離が長く，粒子間の相互作用をほとんど受けず，熱運動の影響のみを受ける。
　気体に熱を与えると，エネルギー保存の法則（熱力学第一法則）に従い，熱量（ Q ）は，仕事（ W ）と内部エネルギー（ U ；粒子の運動エネルギーの総量）の和になる。

　　　　δU ＝ δQ －δW
　　　　δU ：内部エネルギーの変化量，δQ ：外から与えられた熱量，δW ：系外に取り出される仕事

　【熱運動】で紹介したように，気体の粒子の運動は，並進運動（一定速度での直進運動），回転運動，分子内振動に分けられる。
　気体では粒子間の相互作用が小さいので，閉じられた系などの外に対する仕事が小さい場合には，与えられた熱は並進運動の増加使われると考えてよい。
　すなわち，粒子の質量（ m ）は変わらないので，与えられた熱エネルギー（ E ）は，粒子の並進運動の速度（ ν ）の増加（ E ＝ 1 / 2・mν² ）になる。

　気体は多数の粒子の集合体のため，粒子間の距離が離れているとはいえ，粒子同士の衝突がある。気体を構成する原子や分子の衝突は，完全弾性衝突（ perfectly elastic collision ）と考えられるので，衝突により互いのエネルギーを交換する。
　すなわち，一つの粒子に注目した時，ある時に速度 ν1 で移動し，衝突後に速度 ν2 に変わる。これを繰り返しながら存在することになる。従って，ある温度の気体は，幅広い速度分布（マクスウェル分布）を持った粒子の集まりで，粒子の速度はその平均値でしか表せないことになる。
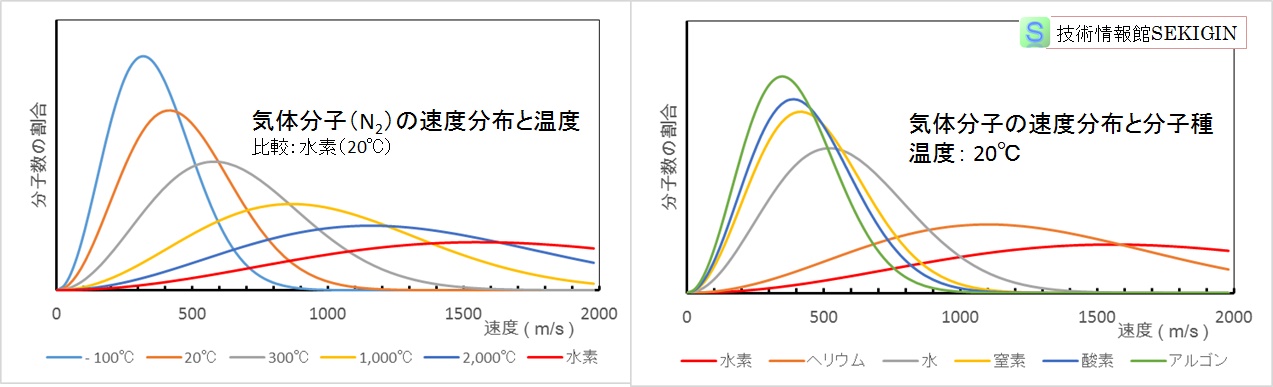
　下図には，窒素分子（ N₂ ）の温度と分子速度の関係，温度 20℃での各種気体分子（ H₂ ，He，H₂O ，N₂ ，O₂ ，Ar ）の速度分布の計算結果を示す。計算には，ボルツマン定数（ 1.3806×10^-23 ），質量として窒素（ 4.6872×10^-26 kg ），水素（ 3.348×10^-27 kg ），ヘリウム（ 6.696×10^-27 kg ），水（ 2.99×10^-26 kg ），酸素（ 5.3568×10^-26 kg ），アルゴン（ 6.6876×10^-26 kg ）を用いた。
　図から，気体分子は，温度が高いほど，分子量が小さいほど，速度分布が広くなり，ピーク速度と平均速度が大きくなることが分かる。

　【参考】
　マクスウェル分布（ Maxwell distribution ）
　熱力学的平衡状態で気体分子の速度が従う分布関数（マクスウェル－ボルツマン分布：Maxwell - Boltzmann distribution ともいう）である。
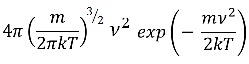
　ここで，分子の質量 m ，ボルツマン定数 k ，温度（ケルビン） T とすると，分子速度νの分布は，次の分布式で表せる。 　マクスウェル速度分布からは，分子速度のピーク ν_max ＝ ( 2 k T / m )^1/2，平均速度ν_ave ＝ ( 4 / π)^1/2ν_max となる。 なお，気体分子運動論における理想気体の単原子分子の二乗平均速度〈ν² 〉＝ 3 k T / m となる。
　衝突（ collision ）
　運動している 2 つの物体が接触し，短時間に力を相互に及ぼし合う物理的現象をいう。 2 つの物体が衝突した時，衝突前の一方の物体の相対速度をνとすると，衝突後の相対速度ν’は，ν’＝ - e νとなる。
　e は反発係数と呼ばれ，0 から 1 の間の値を取る。e ＝ 1 であれば運動エネルギーが保存されるので，完全弾性衝突（ perfectly elastic collision ）といわれる。完全弾性衝突以外は，運動エネルギーの一部が熱エネルギーなどに変換される。