第二部:物質の状態と変化 液体への溶解(基礎)
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,溶質の液体(溶媒)への溶解の限界量を表す【溶解度について】, 【溶解度式】, 【溶解パラメータ】, 【溶解度曲線】 に項目を分けて紹介する。
溶解度について
水に対する食塩や砂糖の溶解は,最も身近に経験される溶解現象である。食塩( NaCl )は,20℃の水 100g に対して約 36g 溶解できる。砂糖(スクロース: C12H22O11 )は,水 100g に対して約 200g 溶解できる。
このように,実用面では,溶質の溶解できる量が重要な情報となる。この溶媒に溶解できる溶質の最大量を溶解度( solubility )という。
溶解度の熱力学的意味
前項の【溶解について】で紹介したように,物質(液体・固体)の溶解は,溶質分子間の相互作用( A-A ),溶媒分子間の相互作用( S-S )が失われ,新たに溶媒和の分子間相互作用( A-Sn )が生まれる過程と考えられる。
一般的に,溶媒和の相互作用エネルギーは,溶質,溶媒の相互作用エネルギーの相乗平均で評価できると考えられるので,エンタルピー変化では不利な過程と考えられる。
しかし,溶質の溶媒への溶解により混合のエントロピーが増加するため,溶媒種,溶質種とある温度の濃度で決まる相互作用エネルギーの効果とが釣り合うまで溶解が進む。この溶質の溶解の限界濃度を溶解度( solubility )である。
溶解度の表記
溶質の状態,即ち固体・液体と気体では溶解度の表記法が異なる。
固体・液体の溶解度
表記は,一定温度( 20 ℃での測定例が多い)で,溶媒 100 g に対する溶質の質量( g )で表記する場合,飽和溶液 100 g に溶けている溶質の質量( g )で表する場合が多い。なお,飽和溶液 100 g に対する溶解度で表した場合には,溶媒量は 100 g から溶解度(溶質の質量)を差し引いた量になる。
溶解度の単位は無名数であるが,一般には溶媒種を明確にするため「 g / 100g ‐溶媒の化学式」等を付して表記する。
歴史的には,溶媒 1 L (リットル)又は 1kg に対する溶質の質量( g )やモル数( mol )で表す例もある。
気体の溶解度
表記には,ブンゼンの吸収係数(一定温度,1 気圧の気体が溶媒 1 ml に溶ける体積を標準状態に換算して表す)の他に,後述の【気体の溶解】で紹介する複数の表記法がある。
一般的には,気体の液体への溶解度は温度の上昇と共に減少する。固体や液体の溶解度と単位が異なるので,これらと比較する場合は不便となる。この場合は,次の要領で単位の換算ができる。
溶媒 100g 当たりの溶質の量に換算する場合は,気体の状態方程式( PV = nRT )から溶媒 1ml 中に含まれる物質量(モル濃度) n を計算し,溶質のモル質量( M )から溶質の質量( m = M × n )を求めるとともに,溶媒の密度(ρ : kg/m3 )から 100 g 当たりの溶媒の体積( X ml = 105 / ρ)を求めることで,溶媒 100 g 当たりの溶解量 m × X が求められる。
参考:溶解の認識について
例えば,高等学校教育など一般的には“水にヘキサンは溶けない”と認識されている。これは,【溶解現象とは】で紹介したように,「似た者同士は相性が良い」の原則から,無極性分子のヘキサンは,極性プロトン性溶媒である水との相性が悪いためこのような認識になっていると考えられる。
実際には,多くの溶媒は,多くの物質を溶解できると考えてよい。問題となるのは,溶液中の濃度が実用上で問題となる範囲にあるかどうかである。
水に対するヘキサンの溶解度(溶解度の表記は複数ある)は,20℃で約 0.0013 g / 100g - H2O ( 13 mg / L )である。この値は,一般的な感覚では“水にヘキサンは溶けない”といっても大きな間違いはないと考えられる。
しかしながら,この溶解度は,水道水の水質基準{有機物(全有機炭素の量:TOC); 3 mg / L以下}と比較して十分に高い濃度であり,水質を問題とする場合にはヘキサンの水への溶解が問題となる。
さらに言うと,溶解度がヘキサンより著しく低い PCB (ポリ塩化ビフェニール:25℃の溶解度 0.0240 mg / 100g - H2O )は,水生環境急性有害性( 96時間の暴露で魚類の半数が死滅する濃度) LC 50が 0.008 mg / L /96H とされ,溶解度より著しく低い濃度( ppt オーダー)であっても環境汚染や健康影響の観点から問題となる。このため,環境分析などの実用上では水への溶解性が無視できない物質として取り上げられる。
【参考】
飽和溶液( saturated solution )
溶解度に達した溶液を飽和溶液( saturated solution )といい,未溶解の溶質と溶液とで溶質分子の溶解と析出の平衡( equilibrium )状態にあるという。ただし,飽和溶液をゆっくり冷却した場合などの溶解の条件によっては,溶解度以上に溶質を溶かした準安定な過飽和( supersaturation )状態になることがある。
ある温度と溶解度曲線の交点の溶液を飽和溶液といい,後述の【固体・液体の溶液平衡】で説明するように,固体表面から溶液中に溶解する粒子(分子,イオン)の数と溶液中から固体表面に析出する粒子の数が等しく,見かけ上の質量変化がない状態をいう。
なお,飽和濃度より低い濃度の状態を不飽和溶液( unsaturated solution ),飽和濃度(溶解度)より高い濃度の状態を過飽和溶液( supersaturated solution )という。
過飽和溶液は,溶液の準安定な状態で,濃度増加が緩やかな時に容易に表れる。この状態では,何らかのきっかけ(容器の凹凸,圧力変動)などで速やかに平衡状態(飽和溶液)に変化(微細な結晶の多量発生など)するので,大きな結晶粒子を得たい場合には,過飽和に至らないよう結晶の成長を促す核となる種結晶( seed crystal )や毛羽立った糸などを用いるのが一般的である。
水道の水質基準
日本の水道は,水道法第 4条の規定に基づき,「水質基準に関する省令」で規定する水質基準に適合することが求められる。省令では, 51の水質基準項目と基準値が定められている。省令では,さらに,水道水中での検出の可能性があるなど水質管理目標設定項目と目標値(27項目),毒性評価が定まらないことや浄水中の存在量が不明等の理由から水質基準項目,水質管理目標設定項目に分類できない要検討項目と目標値(45項目)が定められている。
ページのトップへ
溶解度式
詳細は,篠田耕三 著「溶液と溶解度」(丸善)などの専門書によることとし,ここでは概要のみを紹介する。
溶解熱(混合熱)
ある一定温度でのモル蒸発エネルギーΔE1Vの成分 1 ,モル蒸発エネルギーをΔE2Vの成分 2 を気体状態から凝集し液体にする過程を考える。
それぞれの気体が凝集する際の凝集エネルギーと混合気体を凝集して n1 + n2 モルの溶液を得る際の凝集エネル―の差から混合に要するエネルギーΔEM が求められる。
ここで,分子間力がロンドン分散力(ファンデルワールス力)のみと仮定し,各成分の液体のモル体積を V1 ,V2 とすると,混合に要するエネルギーΔEM は,次式で与えられる。
ΔEM = {n1V1 ・ n2V2 / (n1V1 + n2V2)} × {(ΔE1V / V1)1/2 - (ΔE2V / V2)1/2 }2
ここで,成分 1を溶媒,成分 2を溶質とし,成分 2で偏微分することで,成分 2の 1モル当たりの溶解エネルギー(部分モル溶解エネルギー)が得られる。
ここで,(ΔEV / V)1/2 は,溶解力のパラメータとして適切なため,溶解パラメータ( solubility parameter ;単位 ( cal・cm-2 )1/2 又は MPa1/2 )と称し,δで表される。
部分モル溶解エネルギーは,成分 1の容積分率(体積分率)φ1{ = n1V1 / (n1V1 + n2V2)}を用いて,次式で表される。
V2 φ12 ( δ1 - δ2 )2
溶解度式
正則溶液では,混合による容積変化が小さいので,成分 2の部分モル溶解エネルギーは,成分 2の部分モル溶解エンタルピー(ΔH2 )にほぼ等しいと置けるので,溶解度 χ2{ = n2/(n1+n2)}を用いて,ギブスの自由エネルギー変化は,
ΔG2 ≅ RT lnχ2 + V2 φ12 ( δ1 - δ2 )2
を得る。ここで,成分 2の液体状態のフガシティーを f20 ,溶液と平衡な気相のフガシティーを f2 とすると,溶液と平衡にある成分 2の化学ポテンシャルは,溶液中の成分 2の化学ポテンシャルと等しいので,
RT ln ( f2 / f20 ) = RT ln a2 ≈ RT lnχ2 + V2 φ12 ( δ1 - δ2 )2
が得られる。この式は,溶解度の基本式として知られる。
気体の溶解度
成分 2(溶質)の気体の飽和蒸気圧を P20 ,溶解度を求める時の気体の圧力を P2 とする。
このとき,気体の活量 a2 ≅ P2 / P20 となるので,溶解度の基本式から
ln ( P2 / P20 ) ≈ lnχ2 +{ V2 φ12 ( δ1 - δ2 )2}/ RT
となる。気体の溶解度が小さい場合には,容積分率(体積分率) φ1 ≈ 1 とできる。
従って,飽和蒸気圧 P20 ,溶解度を求める時の気体の圧力 P2 ,温度 T ,溶質のモル体積 V2 ,溶媒と溶質の溶解パラメータ δ が分かれば溶解度が計算できる。
固体の溶解度
溶解度を求めようとする温度 T における過冷の液体状態の成分 2(溶質)の活量を標準とし,固体状態の相対活量 a2S を求める。
成分 2の昇華熱( heat of sublimation )を H2S ,融解熱( heat of fusion )を H2V ,蒸発熱( heat of evaporation )を H2V とすると,
d ln a2S / dT = (ΔH2S - ΔH2V ) / RT2 = ΔH2F / RT2
とできる。ここで,融点( melting point ) Tf 近傍で融解熱が一定であると仮定し積分することで,
ln a2S = -(ΔH2F / R )・{ (Tf - T ) / T・Tf }
を得る。これにより,成分 2の液体及び固体状態の定圧熱容量( CP )が分かれは,温度変化を考慮した固体状態の相対活量 a2S を求めることができる。
従って,固体の溶解度は,気体の溶解度と同様にして,溶解度の基本式を用いて,温度 T ,溶質のモル体積 V2 ,溶媒と溶質の溶解パラメータ δ が分かれば計算できる。
【参考】
フガシティー( fugacity )
高い圧力の実在気体でも,理想気体の化学ポテンシャルの形式が成り立つように導入された圧力の概念で,次のように定義される。
基準圧力(通常は 1気圧)を p0 ,基準圧力での成分 i の化学ポテンシャルをμi0 ,実用圧力での成分 i の化学ポテンシャルをμi,気体定数 R ,温度 T とした時,成分 i のフガシティー fi は,
fi = p0 exp{(μi - μi0)/ RT }
で定義される圧力単位( Pa )の概念である。なお,理想気体では,成分 i の分圧( pi )と等しくなる。
活量( activity )
活量は,ギルバート・ニュートン・ルイス( Gilbert Newton Lewis )によって導入された物理量で,a と表される。活動度と呼ばれる場合もある。
反応の平衡や速度を議論するときに使われる濃度の有効値を指す。なお,一般的には,簡便のため,活量をつぎのように扱うことが多い。
1)希薄溶液において,イオン,分子もその活量は,濃度(モル分率)に等しいとしてよい。すなわち,活量係数 γ= 1 として扱われる。
2)希薄溶液において,溶媒の活量を 1 として差し支えない。
3)溶液と平衡状態にある純粋の固体又は液体の活量を 1 として差し支えない。
4)溶液と平衡関係にある気体の活量は,その気体の分圧に等しい。
5)混合液体の平衡を考える場合,その一成分の活量は,そのモル分率に等しい。
ギルバート・ニュートン・ルイスは,アメリカ合衆国の物理化学者( 1875 ~ 1946年)で,共有結合の発見(ルイスの電子式),ラジカル(不対電子対)の定義,酸・塩基の定義(ルイス酸・塩基),熱力学の再構築による化学熱力学の提唱,光化学実験,光子( photon )の命名などで知られる。
活量係数( activity coefficient )
理想とする数値(活量)からのずれを表す指標として,活量係数γが定義される。i 成分の活量 ai と理論上のモル分率χi の間には次の関係にある。
a i = γi χi
ページのトップへ
溶解パラメータ
溶解度は,上述のように,混合のギブスの自由エネルギー変化を求めるなどの熱力学的なアプローチにより求めることが可能である。
しかし,実際の溶液では,分子間力がロンドン分散力(ファンデルワールス力)のみの正則溶液では扱えない場合が多い。さらに,エネルギー変化の精密かつ迅速な測定が困難で,溶媒選択などの実用に供せるほどのデータ蓄積に至っていない。このため,溶媒選定の際には,測定された溶解パラメーターや経験則によって行われることが多い。
溶解パラメータ( solubility parameter )
溶解パラメータ SP値( solubility parameter )は,溶解度パラメータ,ヒルデブラントの溶解パラメータ( Hildebrand solubility parameter )とも呼ばれる。
溶解パラメータの単位には,当初から用いられる ( cal・cm-3 )1/2 の他に,SI単位系を用いた MPa1/2 が用いられ,混在しているのが現状である。
なお,1 cal・cm-3= 4.18605 J・cm-3= 4.18605 N・m・cm-3= 4.18605×106 N・m-2= 4.18605 MPa,従って,1 ( cal・cm-3 )1/2 = 2.04598 MPa1/2 となる。
上述したように,溶解のギブスの自由エネルギー変化は,
ΔG2 ≅ RT lnχ2 + V2 φ12 ( δ1 - δ2 )2
で表されることを示した。この基本式からは,成分 1(溶媒)と成分 2(溶質)の溶解パラメータ δの差が小さいほど,混合熱が小さく,混合によるギブスの自由エネルギー変化を小さくできること,すなわち,溶質をよく溶かす溶媒の選定には,溶質の溶解パラメータに近い値を持つ溶媒を選択すればよいことが分かる。
溶解パラメータの求め方
ヒルデブラントの溶解パラメーター δの値は,ヒルデブランド( Hildebrand )らによって多数の化合物について求められ,下記の参考文献 1)~3) などに報告されている。溶解パラメータの算出方法には,蒸発熱,蒸気圧,固体の溶解度,ヒルデブランド則,内部圧,臨界定数,表面張力などとの相関関係を利用したものが知られている。ここでは,蒸発熱,蒸気圧,固体の溶解度を用いた算出方法の概要を紹介する。
蒸発熱から求める方法
液体の飽和蒸気圧が低い場合, 液相と平衡にある蒸気相は事実上理想気体とみなせる。この場合には,ΔHV - RT = ΔEV の関係が用いられ,蒸発熱 ΔHV から溶解パラメータ―が求まる。
δ =(ΔEV / V)1/2 = {(ΔHV - RT ) / V }1/2
蒸気圧から求める方法
溶解度を知りたい温度の蒸発熱の値がない場合も多い。この場合は,蒸気圧の温度依存性に関する下記のクラウジウス・クラペイロンの式( Clausius-Clapeyron equation )を用いて求めた見掛けの蒸発熱を用いて間接的に計算できる。
d ln P / dT = ΔHV / PTΔVV = ΔHappV / PT2
ここで ΔVV は 気液の分子容差,ΔHappV は 蒸気圧曲線の勾配から求まる見掛けの蒸発熱である。
固体の溶解度から求める方法
融点が高く室温で固体の化合物の溶解パラネーターは,固体の溶解度データを利用する。すなわち, 溶質(成分 2 )と正則溶液を形成できる溶媒(成分 1 )を選定し,その溶媒における溶解度データ(χ2 )と溶媒の溶解パラメーター(δ1 ),容積分率(体積分率;φ1 )を前述の溶解度の基本式に代入することで,溶質の溶解パラメーター(δ2 )を求めることができる。
この原理は,溶質の溶解パラメーター(δ2 )は,溶媒に寄らず一定の値になることを前提にしている。
【参考文献】
1) J.H. Hildebrand, R.L. Scott,“Solubility ofNonelectrolytes”, 3rd ed., Reinhold, New York(1958).
2) J.H. Hildebrand, R.L. Scott,“Regular Solutions”, Prentice-Hall, Englewood Cliff, N.J,(1962).
3) J.H. Hildebrand, J.M. Prausnitz, R.L. Scott,“Regular and Related Solutions”, Van Nostrand-Reinhold, New York (1970).
ハンセンの溶解パラメータ( Hansen solubility parameter, HSP )
ヒルデブラントの溶解パラメーター( SP )は,正則溶液が成り立つ溶媒,すなわち,極性が無く,水素結合を持たない溶媒にしか適用できない。水などの極性溶媒や水素結合を持つ溶媒に対しては,これらを考慮したハンセンの溶解パラメーター( Hansen solubility parameter, HSP )が用いられる。
ハンセンの溶解パラメーター( HSP )は,次の 3 つのパラメーター(分散力項,極性項,水素結合項)で構成されている。
分散力項(δD): 分子間の分散力によるエネルギー
極性項(δP) : 分子間の双極子相互作用によるエネルギー
水素結合項(δH) : 分子間の水素結合によるエネルギー
ヒルデブラントの溶解パラメーター SP (δ)とハンセンの溶解パラメーター HSP (δD,δP,δH)には,次の関係がある。
δ2 = δD2 +δP2 +δH2
ハンセンの溶解パラメーター( HSP )は,混合溶媒の溶解度パラメータ予測などに有効で,溶媒と有機高分子材料との相互作用が問題となる塗料,接着剤,プラスチック材料などの分野で古くから用いられている。
実用を重視した溶解パラメータ( SP値,HSP値)の求め方や活用例などについては,(株)情報機構出版の「溶解性パラメーター適用事例集~メカニズムと溶解性の評価・計算例等を踏まえて~」,山本秀樹著「 SP値 : 基礎・応用と計算方法」, (株)R&D支援センター出版の大佐々 邦久著「溶解度パラメータ (SP値・HSP値)の求め方と微粒子の分散安定化への活用術」などの多数の出版物,技術セミナーがある。
ページのトップへ
溶解度曲線
溶解度曲線
溶解度曲線とは,物質の溶解度と温度との関係を図示したもので,一般的には,縦軸に溶解度,横軸に溶媒の温度を示す。
溶解度は,溶媒和によるエンタルピー変化と溶質の溶媒への溶解による混合のエントロピーのバランスで決まることを紹介した。
従って,溶解度と温度の関係は,溶質と溶媒との関係により,温度の上昇で溶解度が増加(右上がりのグラフ)する物質,ほとんど変化しない物質,温度の上昇と共に溶解度が減少(右下がりのグラフ)する物質に分けられる。
溶解度と温度の関係を明らかにすることで,再結晶効率の検討,溶質と溶媒との相互作用の変化などの理解が容易となる。
水への溶解例
溶質の質量を無水物として表記するので,例えば硫酸銅(Ⅱ)五水和物( CuSO4・5H2O )など結晶水(水和水)を持つ化合物の水への溶解度では,水和水は溶媒の量として計算される。
多くの固体物質は温度の上昇と共に溶解度が増す右上がりのグラフとなる。しかし,水酸化カルシウムや硫酸セリウムのように温度と共に溶解度が減少(右下がりの変化)を示すものもある。また,硫酸ナトリウムのように,特定温度(この場合は 34.38 ℃)で溶解度のピークを持つものもある。
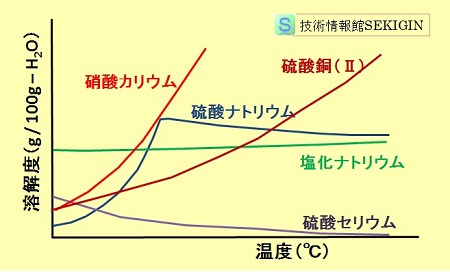
溶解度曲線の例
ページの先頭へ