第二部:物質の状態と変化 希釈溶液の性質
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,理想溶液に準じる理想希薄溶液の束一的性質として知られる沸点上昇現象について,【沸点と飽和蒸気圧】, 【溶液の沸点上昇】, 【沸点上昇の熱力学的扱い】, 【ファントホッフの因子】 に項目を分けて紹介する。
沸点と飽和蒸気圧
沸点とは
JIS K 0211 「分析化学用語(基礎編)」には,沸騰( ebullition )を“一定圧力のもとで液体がある一定温度に達し,液体内部から気化が起こる現象。沸騰の起こる温度を沸点という”と定義している。
この定義に従うと,沸騰点ともいわれる沸点( boiling point )は,液体が沸騰し始めるときの温度をいう。
厳密には,一定圧力のもとで飽和蒸気とその液体とが平衡を保って共存する温度のことであるが,地上で試験する限り,沸騰の定義にある液体内部からの気化が起きるためには,液体内部の圧力が外気の圧力より僅かに高い(液面からの深さに応じる)ので,沸点より僅かに高い温度で,現象としての沸騰が観察される。
ここでは,気相の圧力と液体の飽和蒸気圧が等しくなる温度を沸点とする。なお,圧力が 1 気圧( 101.315 kPa )のときの沸点を明示するため,標準沸点( normal boiling point,NBP )と称する場合もある。
飽和蒸気圧とは
広義には,蒸気(気体)の示す圧力(蒸気張力)をいう。
一般には,単に蒸気圧と称した場合でも,液体と平衡状態にある気体(蒸気)の飽和蒸気圧( saturated vapor pressure )を指すことが多い。
液体の飽和蒸気圧とは,物質の相と温度・圧力などの熱力学的な状態量との関係を表す相図(phase diagram)において,気相と液相の境界(蒸気圧曲線; vapor pressure curve )と温度との交点の圧力をいう。
飽和蒸気圧は,温度によって定まる物質固有の値をもち,一般に温度とともに増大する。その定量的関係は,クラペイロン-クラウジウスの式( Clapeyron-Clausius' equation )で与えられる。
クラペイロン-クラウジウスの式は,圧力 P ,熱力学的温度 T において,気相と液相が熱平衡にある時の相転移に伴うエンタルピー変化 ΔH (転移熱),体積変化 ΔV とした時,
dP / dT = ΔH / ( TΔV )
で表される。ここで,気相・液相の相平衡の転移熱(モル蒸発熱)を ΔHV , 気体のモル体積 Vg ≫液体のモル体積 Vl とした時,
ΔH = ΔHV = 一定 ,ΔV = Vg - Vl ≅ Vg
と仮定できる。また,理想気体 1mol では,PVg = RT が成立するので,
dP / dT = ΔH / ( TΔV ) ≅ ΔHV・P / ( R・T2 )
とできる。初期条件として,既知の液体の沸点 ( TB ) での蒸気圧 ( P0 ) を与えて解くと,
in( P / P0 ) = -(ΔHV / R )・( T-1 - TB-1 )
とでき,相図(状態図)における気-液曲線の関係が得られる。
ページのトップへ
溶液の沸点上昇
前項の【蒸気圧降下】で紹介したように,蒸気圧が溶媒より著しく低い溶質(不揮発性溶質)が溶けた溶液の飽和蒸気圧は,純溶媒の飽和蒸気圧より減少する。
従って,溶液の蒸気圧が減少することで,飽和蒸気圧が気相の圧力と同じになる沸点が上昇することを意味する。
不揮発性溶質がわずかに溶けた溶液の沸点が上昇する現象を沸点上昇( elevation of boiling point )といい,純粋な溶媒の沸点と希薄溶液の沸点の差( ΔT )を沸点上昇度という。
希薄溶液で沸点近くの狭い温度範囲を考えれば,純溶媒と溶液の蒸気圧曲線(蒸気圧の温度依存性)は,多くの場合に近似的に曲線の傾きが等しいと考えてよい。
従って,下に示す模式図のように,希薄溶液の沸点上昇度(ΔT : K ケルビン )は,蒸気圧減少(ΔP )と比例関係にあるとみなすことができる。
前項の【蒸気圧低下】で紹介した蒸気圧減少量(ΔP ≒ 1000 P*0 M0 ( nA / 1000 W ) = K m )との比例係数をαとし,
ΔT = αΔP ≒α K m
と表すことができる。ここで,α K = Kb と置くと,溶質の質量モル濃度 m ( mol / kg )との関係は,
ΔT ≒ Kb m
となる。この時の Kb は,モル沸点上昇( molar elevation of boiling point )や沸点上昇定数と呼ばれ,溶媒の種類に依存するが,溶質の種類には依存しない値で,1キログラムの溶媒に 1モルの不揮発性の溶質が溶けている溶液の沸点上昇度(単位; K・kg / mol )を意味する。
ただし,溶質が電解質など複数の粒子に分かれる物質の場合は,質量モル濃度 mについては,後述するファントホッフの因子を導入した補正が必要である。
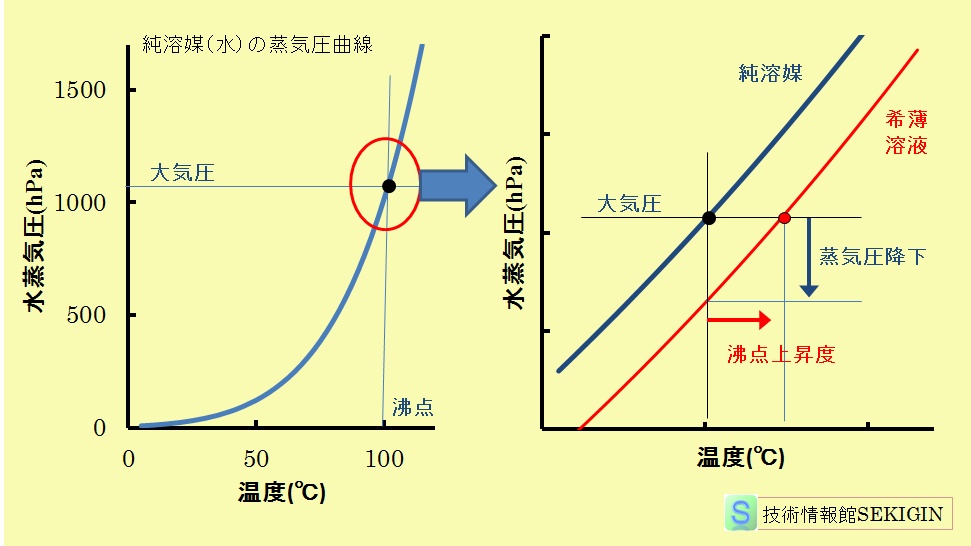
蒸気圧降下,沸点上昇原理の模式図
| 溶媒名 | 化学式 | 分子量 | 沸点(℃) | モル沸点上昇 |
|---|---|---|---|---|
| 水 | H2O | 18.02 | 99.98 | 0.515 |
| メタノール | CH3OH | 32.04 | 64.7 | 0.785 |
| エタノール | C2H5OH | 46.07 | 78.37 | 1.16 |
| アセトン | CH3COCH3 | 58.08 | 56.5 | 1.71 |
| ベンゼン | C6H6 | 78.11 | 80.1 | 2.53 |
| クロロホルム | CHCl3 | 119.4 | 61.2 | 3.62 |
| 四塩化炭素 | CCl4 | 153.82 | 76.8 | 4.48 |
ページのトップへ
沸点上昇の熱力学的扱い
希薄溶液の溶質がすべて不揮発性のとき,沸点上昇度 ΔT は,溶媒固有の性質と溶質のモル分率の総和で決まり溶質の種類に依らない(束一的性質)。
化学ポテンシャルを用いた説明
純溶媒 A の気液平衡では,圧力 P における純溶媒の沸点を T0bp とした時,気相の化学ポテンシャルは,液相の化学ポテンシャルに等しい。
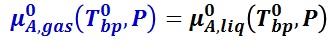
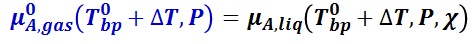
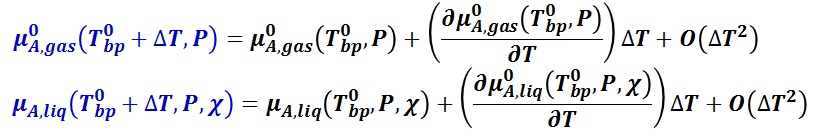
エントロピー s と化学ポテンシャル μ には,s = -∂μ/∂T の関係があるので,
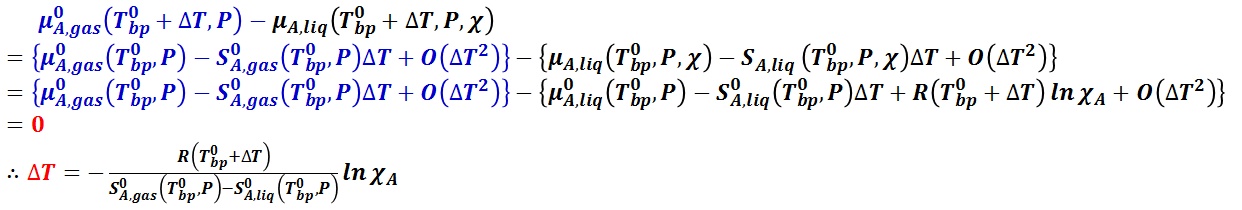
沸点における気相と液相のエントロピー差と純溶媒の沸点におけるモル蒸発エンタルピー ΔvapH0m(T0bp, P) との次の関係,
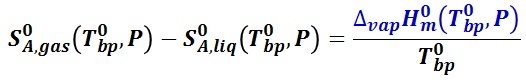
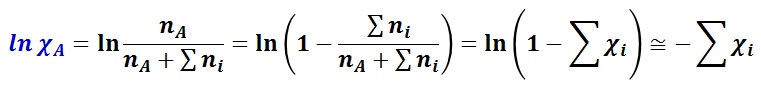
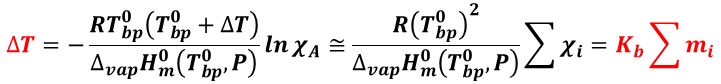
すなわち,沸点上昇度は溶質のモル濃度( mi )の総和に比例し,比例係数(モル沸点上昇 Kb )は溶媒の性質のみで決まる。
【参考】
テーラー展開( Taylor expansion )
真の値とは異なるが,ほぼ等しい数値を求めるために行う関数の近似方法の一つ。何回でも微分可能な関数に対して用いられる。
関数 f( x )が x = a の近傍で定義され、そこで n 回微分可能であるならば,f( x )は次の様に表すことができる(テーラーの定理)。この形式で表記することをテーラー展開という。
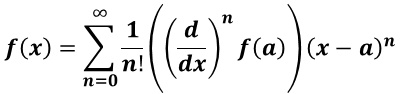
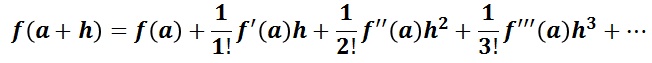
ページのトップへ
ファントホッフの因子
溶質が電解質の場合
沸点上昇度は,溶液に溶けている溶質の濃度,言い換えれば粒子の数に比例する。従って,電解質などは,溶質のモル濃度に対し,電離の程度を考慮した補正が必要になる。
例えば,1 mol の塩化ナトリウム( NaCl )を 1 kg の水に溶解した場合に,塩化ナトリウムの質量モル濃度は 1 mol / kg であるが,水中では,ほぼ完全に NaCl → Na+ + Cl- に電離しているため,質量モル濃度として 2 mol / kg に相当する粒子数が存在することになる。
電解質 AxBy の場合は,水中で AxBy ⇆ xAy+ + yBx- に解離するが,すべての電解質が完全に解離するとは限らない。そこで,部分的に解離している状態を表現するため,電離度(α)という概念が導入される。
電離度(α)=(電離している電解質の物質量)/(溶けている電解質全体の物質量)
完全に解離している場合は,α= 1 になる。
一般に,電解質の組成式が ( x + y ) 個のイオンからなるとき,電解質 m ( mol / kg ) の溶液の電離度をαとすると,電離後に生じる粒子の質量モル濃度は,
m ×{ 1 + ( x + y - 1 ) α}( mol / kg )
になる。ここで,{ 1 + ( x + y - 1 ) α}をファントホッフの因子という。
【参考】
電離度( degree of ionization )
実際に電離している物質のモル比を示したもの。記号 αで表すことが多い。
電離度が 1 に近い物質を強電解質 ( strong electrolyte ) ,電離度の小さい物質を弱電解質 ( weak electrolyte ) という。
電離度は,濃度の影響を大きく受けるため,物性の指標としては扱いにくい。
ページの先頭へ