第二部:物質の状態と変化 気体の量と体積
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,実在気体の状態方程式について,【分子の大きさに対する補正】, 【分子間力の補正】, 【ファンデルワールスの状態方程式】 に項目を分けて紹介する。
分子の大きさに対する補正
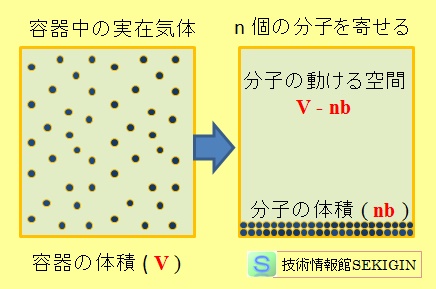
実在気体の実効体積
このため,ファンデルワールスの状態方程式,ビリアル方程式,ディーテリチの状態方程式,ペン=ロビンソンの状態方程式,レドリッヒ=クオンの状態方程式など,様々の状態方程式が提唱されている。
ここでは,その中で最も知られるファンデルワールスの状態方程式における補正の考え方を次に紹介する。
分子の大きさに対する補正
実在気体に加える圧力を増加してゆくと,体積が減少し,ついには液体になる。液体に圧力を加えてもその体積はほとんど変化しない。
すなわち,実在気体の分子が自由に動ける空間は,容器の体積( V )から分子の体積を差し引いた体積と考えることができる。
すなわち,容器内の気体分子の物質量( n モル),1モル当たりの分子の体積( b )とから,気体分子が自由に動ける空間の体積は,( V – n b )とできる。従って,分子の体積が影響する場合に,状態方程式は,
P ( V – n b ) = nRT
と補正すればよい。
ページのトップへ
分子間力の補正
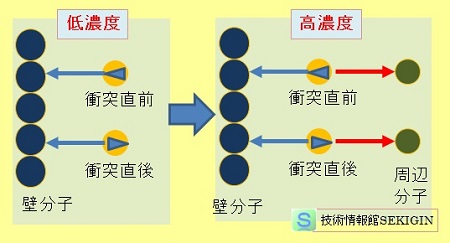
気体濃度と分子間相互作用
気体の濃度が低い場合(低圧)は,気体分子相互の影響をほとんど受けずに,気体分子が容器の空間を自由に飛翔する。
一方,気体の濃度が高い場合(高圧)は,壁に衝突する分子が,その周辺の気体分子から壁と反対方向に引力を受ける。これにより,壁に衝突した気体分子の壁に加える力(測定される圧力)が弱まる。
すなわち,測定される圧力 P は,実際の圧力から分子間力の影響を除いた値となる。
分子間力は,気体の濃度( n / V )に比例し,壁に衝突する分子数も気体の濃度( n / V )に比例する。
従って,測定された圧力は,分子間力×衝突数の影響を受けると考えられるので,比例係数( a )とすると,実際の圧力は,測定圧力 P に分子間力の影響( a ( n / V ) 2 )を加えた値になると考えられる。
従って,状態方程式は,
( P + a n 2 / V 2 ) V = nRT
と補正すればよい。
ページのトップへ
ファンデルワールスの状態方程式
実在気体では,分子の大きさと分子間力の影響を同時に受けるので,状態方程式の補正は,
( P + a n 2 / V 2 ) ( V - n b ) = nRT
となり,これをファンデルワールスの状態方程式という。
主な気体分子の係数 a ( pa ・ m6 ・ mol-2)と 係数 b ( m3 ・ mol-1 )は,次の通りである。
分子量の順番に並べると,
水素( H2 : a = 24.8 × 10-3 ,b = 26.7 × 10-6 ),
ヘリウム( He : a = 3.45 × 10-3 ,b = 23.8 × 10-6 ),
窒素( N2 : a = 141 × 10-3 ,b = 39.2 × 10-6 ),
空気( air: a = 135 × 10-3 ,b = 36.6 × 10-6 ),
酸素( O2 : a = 138 × 10-3 ,b = 31.9 × 10-6 ),
水蒸気( H2O : a = 553 × 10-3 ,b = 33.0 × 10-6 ),
二酸化炭素( CO2 : a = 365 × 10-3 ,b = 42.8 × 10-6 )
分子の大きさの影響を受ける係数 b の順位は,He < H2 < O2 < H2O < air < N2 < CO2で,
分子間力の影響を受ける係数 a の順位は,He < H2 < air < O2 < N2 < CO2 < H2O である。
【参考】
ファンデルワールスの状態方程式( van der Waals equation )
オランダの物理学者ヨハネス・ディーデリク・ファン・デル・ワールス(Johannes Diderik van der Waals, 1837年~1923年)は,分子の大きさと分子間力を考慮した気体の状態方程式を 1873年の博士論文「液体と気体の連続性について」の中で提唱した。
P = nRT/( V - n b )-a n 2 / V 2
ビリアル方程式( virial equation )
気体の状態を,とくに高圧または凝縮温度付近まで精度よく表すために用いられる状態式の一つで,気体の圧力およびモル体積をそれぞれ P , V としたとき,モル体積 V の逆数の冪級数(べききゅうすう: power series )に展開するビリアル展開( virial expansion )で表した方程式。
PV = nRT(1+B/V+C/V2+・・・)
B,C,・・・は,それぞれ第二ビリアル係数,第三ビリアル係数・・・という。ビリアル係数( virial coefficient )は,体積に依存しない温度だけの関数である。
ディーテリチの状態方程式( Dieterici equation )
実在気体の圧力と体積との関係を表す式の一つ。
P・exp ( na/RTV ) = nRT/( V − nb )
a , b は定数で,定圧条件ではファンデルワールスの状態方程式と同じ形になる.
ペン=ロビンソンの状態方程式( Peng-Robinson equation )
ペン ( Ding-Yu Peng ) とロビンソン ( Donald B. Robinson ) が提案したファンデルワールスの状態方程式を発展し,高圧条件下で用いられる状態方程式。
P = RT/(v-b) - aα/{v(v+b) + b(v-b)}
レドリッヒ=クオンの状態方程式( Redlich–Kwong equation )
化学工学で用いられるファンデルワールスの状態方程式を改良した状態方程式。
P = nRT/( V - n b )-a n 2 /{ T0.5 V(V+nb) }
ページの先頭へ