第二部:物質の状態と変化 気体の量と体積
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,複数の分子種で構成される混合気体について,【混合気体の状態方程式】, 【分圧の法則】, 【分体積の法則】 に項目を分けて紹介する。
混合気体の状態方程式
空気をはじめ,実在気体の多くは,複数の気体分子が混合した気体である。
ここで,3 種類( A ,B ,C )の気体が混合した気体が一定容量( V )の容器に入っていると仮定する。この時の容器内の圧力を混合気体の全圧という。
混合気体が理想気体として扱える範囲の圧力と温度にある場合に,気体の種類 A ,B ,C と圧力,体積の関係を考える。
気体の状態方程式( PV = nRT )は,気体の種類によらず適用できること,同一圧力,同一温度,同一体積のすべての種類の気体には同じ数の分子が含まれる(アボガドロの法則)ことは既に紹介した。
すなわち,気体の状態方程式は,気体の種類によらず,容器に入っている気体分子の量(数)のみに依存することが分かる。
ページのトップへ
分圧の法則
アボガドロの法則より,容器内の物質量 n は,気体種類は関係ないので,それぞれの物質量の単純和とできる。すなわち,容器内の気体 A の物質量 nA モル,気体 B の物質量 nB モル,及び気体 C の物質量 nC モルとすると,混合気体の物質量 n = nA + nB + nC モルとなる。
従って,気体の状態方程式は,
PV = nRT = ( nA + nB + nC ) RT = nA RT+ nB RT+ nC RT = PA V+ PB V+ PC V
とできる。
すなわち,P = PA + PB + PC となる。
ここで,PA ,PB ,PC は,それぞれの気体種の分圧( partial pressure )という。
この関係をまとめると,「混合気体全体の圧力(全圧)は,各気体成分の圧力(分圧)の和に等しい。」となる。これを分圧の法則( law of partial pressures ),又はドルトンの法則( Dalton's law )という。
ちなみに,PA V = nA RT = ( nA / n )・n RT = ( nA / n )・PV とできるので,気体成分の分圧は,全圧とモル分率( nA / n : 気体 A のモル分率という)から容易に求めることができる。
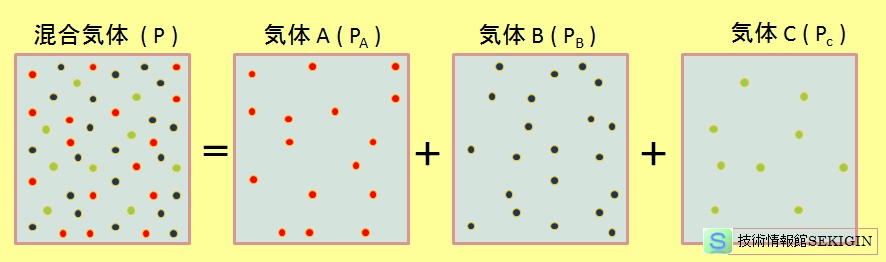
分圧の法則(体積一定)
ページのトップへ
分体積の法則
分圧の法則と同じように考えることができる。すなわち,気体の状態方程式から,
PA V = nA RT = P VA
従って, V = VA + VB + VC
と,圧力と体積の関係を入れ替えた関係が得られる。
この関係は,「理想気体において,混合気体の体積は,同温同圧の成分気体の体積の和に等しい。」と表現でき,分体積の法則,又はアマガーの法則( Amagat's law )といわれている。
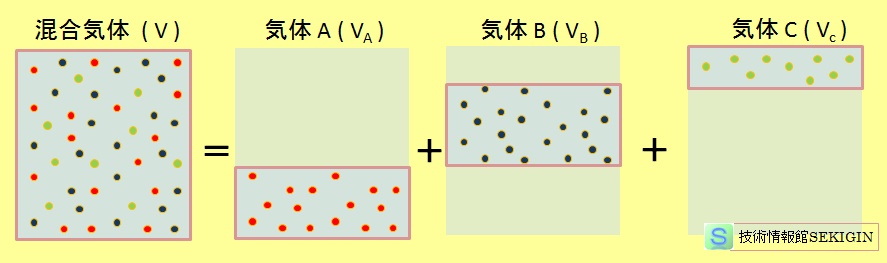
分体積の法則(圧力一定)
ページの先頭へ