第二部:物質の状態と変化 液体への溶解(基礎)
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,溶質が固体の一般的な場合の溶解について,【固体・液体の溶解平衡】, 【溶解平衡の利用(固体の精製)】, 【溶解平衡の利用(化学分析)】 に項目を分けて紹介する。
固体・液体の溶解平衡
溶解平衡とは
溶媒と接触する溶質(固体)の表面(界面)では,前項で紹介したように,強い分子間力で拘束されていた粒子が,溶媒和した粒子(分子,又はイオン)として溶液中に離脱する現象(溶解反応)と溶液中の溶媒和した粒子が固体表面に衝突し,固体に拘束される現象(析出反応)が同時に起きる。
すなわち,溶解現象は,溶解反応と析出反応との可逆反応( reversible reaction )と考えられる。
化学反応の速度は,反応物,生成物の濃度と温度に影響される。温度が一定の場合は,反応速度定数( k )は,濃度によらず一定である。
例えば,固体の溶質( M(s) )が水( aq )に溶解する現象は,
溶解反応 : M(s) + aq → M(aq) : 反応速度 ν1 = k1 { M(s) } { aq }
析出反応 : M(aq) → M(s) + aq : 反応速度 ν2 = k2 { M(aq) }
と表現できる。なお,{ } は,各物質の活量である。固体と溶媒である水の活量は 1 とできるので,溶解の反応速度は,ν1 = k1 と,温度で決まる一定速度で溶解する。
一方,析出反応は,溶解が進むと共に増加する { M(aq) } に比例し析出の反応速度が増加する。遂に,析出の反応速度が ν2 = ν1 となった段階で,見かけ上で { M(aq) } が増加しなくなる。すなわち,
ν1 = ν2 ∴ k1 { M(s) } { aq } = k2 { M(aq) }
となる。この状態を平衡状態(溶解平衡)といい, { M(aq) } / { M(s) } { aq } = k1 / k2 = K を平衡定数という。反応速度定数は,濃度に寄らず温度で決まる定数であるから,平衡定数も温度で決まる定数となる。
溶解平衡に至る時間について
溶解平衡に至る時間は,上記の反応速度の他に,溶液内での溶質の拡散が影響する。この状況は,模式的に次のように考えられる。
外部からのエネルギー授受が無い場合には,下図に示すように,固体表面から液体中に溶媒和した溶質粒子が一定の溶解速度で溶出する。このため,固体表面近傍の溶質濃度が増加する。
溶質濃度の増加に伴い,溶液中の溶質粒子が固体表面に析出する反応が進む。一方で,固体表面近傍から沖合に向って溶質の濃度勾配(concentration gradient)が発生することになる。この濃度勾配は,時間と共に変化するので,一般的に,Fickの第二法則に従うと考えられている。
従って,拡散が進み,固体表面近傍と沖合の溶液の濃度勾配がなくなるまで,溶解平衡に達しないと考えられる。すなわち,溶解平衡に至る時間は,溶液中での溶質の拡散に依存することになる。このため,実用上では,撹拌などの拡散を物理的に促進する方法が用いられる。
異なる液体同士を接触させた場合も,液体 / 液体界面で同様の現象が起きていると考えられる。
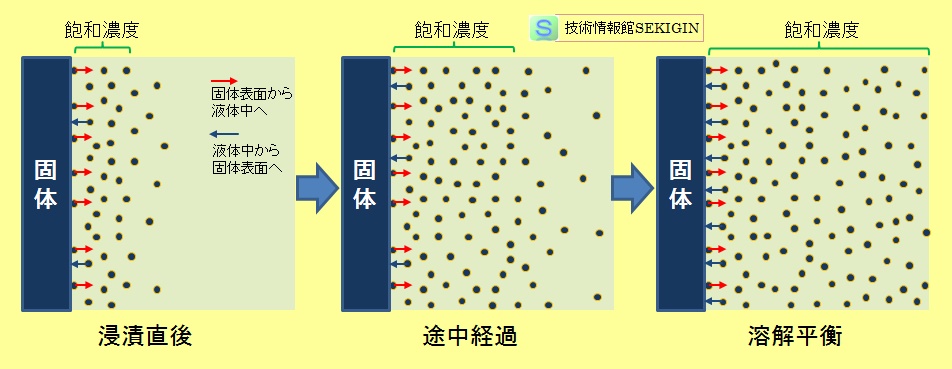
溶解現象の模式図(溶解平衡)
フィックの法則(Fick's laws of diffusion)
気体,液体のみならず固体(金属)にも適用できる物質の拡散に関する基本法則である。フィックの法則には第 1法則と第 2法則がある。
フィックの第 1法則
“拡散束(流束;flax)は,濃度勾配に比例する”と表現される法則で,定常状態拡散(濃度が時間で変わらない)で適用される。拡散係数を D ,位置 x での濃度 c とした時,拡散束 J は,J = − D grad c あるいは J = − D ( dc /dx ) で与えられる。
フィックの第 2法則
実際の拡散で見られる濃度が時間に関して変わる非定常状態拡散に適用される。拡散係数 D が定数のとき,濃度 c の時間変化は,∂c /∂t = − div J = D∇2 cあるいは∂c /∂t = D (∂2 c /∂x2 ) で与えられる。
拡散係数(diffusion coefficient)
物質の拡散に関し,拡散量と濃度勾配の関係を与えるフィックの法則で定義される比例項で,拡散する分子の平均速度で,物質の拡散の早さの指標と考えられる。
ページのトップへ
溶解平衡の利用(固体の精製)
上記で溶解平衡は,温度に依存する溶解反応の速度定数と析出反応の速度定数の比である平衡定数で決まることを紹介した。
溶解平衡に至った溶液の濃度,すなわち溶解度は,温度で決まる溶媒和によるエンタルピー変化と溶質の溶解による混合のエントロピー変化のバランスで決まることを紹介した。
実用上の問題として,不純物を多く含む固体を精製し純度の高い固体を得ること,溶液中に含まれる成分の分析などに溶解現象が利用される。固体の精製には,溶解度と温度の関係を示す溶解度曲線の特性を利用した再結晶化が利用され,成分分析には,分析対象の成分と溶解度積の小さい成分の添加による沈殿反応が利用される。
再結晶化法
不純物の混入した固体を精製する再結晶法による固体の精製は,溶解度曲線で溶解度が大きく変わる温度範囲のある物質に対しては,温度を変える方法が有効である。
一方,溶解度曲線の温度依存性が低い塩化ナトリウム( NaCl )などは,温度変化による精製高効率が悪いため,再結晶による精製は,溶液中の濃度を変えるため,煮詰めるなど溶媒を揮発させる方法が採られる。
なお,再結晶化法は,対象物質と不純物の溶解度の差が小さい場合には不適切である。
ここでは,温度変化で溶解度が急激に変化する硝酸カリウム( KNO3 )と変化がより緩慢な硫酸銅(Ⅱ)( CuSO4 )の混合物から,純度の高いそれぞれの物質を得る再結晶法について溶解度曲線を用いて解説する。
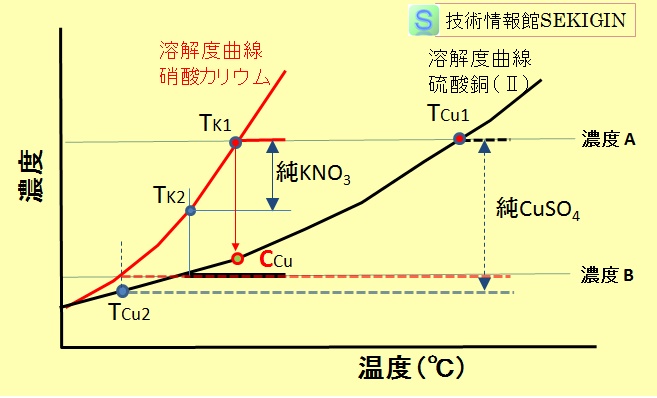
再結晶による精製の原理
温度に対する溶解度変化の緩やかな硫酸銅(Ⅱ)(濃度 A )に不純物として濃度変化の大きい硝酸カリウムが少量(濃度 B )含まれている固体を考える。
硫酸銅(Ⅱ)の溶解度曲線の濃度 A と交差する温度( TCu1 )以上に加熱することで,すべての固体を溶解することができる。
すべての固体が溶解した後に,溶液の温度を徐々に下げてゆくと,温度( TCu1 )で硫酸銅(Ⅱ)が析出し始める。
温度が,硝酸カリウムの溶解度曲線と濃度 B が交差する温度( TCu2 )まで下がると,硝酸カリウムの析出が始まる。
従って,温度( TCu2 )に至るまでは,溶解度曲線の濃度差に相当する量の純粋な硫酸銅(Ⅱ)を得ることができる。
なお,大きな結晶を得たい場合は,過飽和とならないように,トリガーとなる結晶核などがあるとスムーズに実験できる。
純粋な硝酸カリウム結晶を得るには
温度に対する溶解度変化の大きい硫酸カリウム(濃度 A )に不純物として濃度変化の比較的緩やかな硫酸銅(Ⅱ)が少量(濃度 B )含む固体を考える。
硝酸カリウムの溶解度曲線の濃度 A と交差する温度( TK1 )以上に加熱することで,すべての固体を溶解することができる。
すべての固体が溶解した後に,溶液の温度を徐々に下げてゆくと,温度( TK1 )で硝酸カリウムが析出し始める。
温度が,硫酸銅(Ⅱ)の溶解度曲線と濃度 B が交差する温度( TK2 )まで下がると,硫酸銅(Ⅱ)の析出が始まる。
従って,再結晶法の操作を温度( TK2 )までにとどめることで,温度( TK1 )と止めた温度の硝酸カリウムの濃度差に相当する量の純粋な硝酸カリウムを得ることができる。
図から分かるように,硫酸銅(Ⅱ)の濃度が,温度( TK1 )と溶解度曲線との交点の濃度( CCu )を超える場合には,この方法で純粋な硝酸カリウムを得ることができない。
ページのトップへ
溶解平衡の利用(化学分析)
上記で溶解平衡は,温度に依存する溶解反応の速度定数と析出反応の速度定数の比である平衡定数で決まることを紹介した。
溶解平衡に至った溶液の濃度,すなわち溶解度は,温度で決まる溶媒和によるエンタルピー変化と溶質の溶解による混合のエントロピー変化のバランスで決まることを紹介した。
実用上の問題として,不純物を多く含む固体を精製し純度の高い固体を得ること,溶液中に含まれる成分の分析などに溶解現象が利用される。固体の精製には,溶解度と温度の関係を示す溶解度曲線の特性を利用した再結晶化が利用され,成分分析には,分析対象の成分と溶解度積( Ksp )の小さい成分の添加による沈殿反応が利用される。
沈殿反応
原理
沈殿反応とは,溶解反応をの見方を変えたものである。例えば塩化銀( AgCl )の沈澱反応は次のように表現される。
Ag+ (aq)+ Cl-(aq)⇔ AgCl ↓+ aq
式中の ↓ は,固体として沈殿することを意味する。
銀イオン( Ag+ )を含む分析対象溶液に,塩化物イオンを添加し,析出した固体( AgCl )の乾燥重量を計測することで,溶液に含まれる銀イオン量を定量分析できる。
溶液中に他のイオンを含まない場合
溶液中に沈殿反応と関係ない他のイオンを多量に含まない場合は,実用的には活量係数を考慮しなくとも大きな問題を生じない。すなわち,銀イオン濃度と塩化物イオン濃度の積 [Ag+] [Cl-] が溶解度積 Ksp 値 1.7×10-10 より大きい場合に固体の塩化銀( AgCl )が沈殿する。
ここで,添加した塩化物イオンの濃度を X mol / L とした場合,固体として沈殿せずに溶液に残存する銀イオンの濃度は,
[Ag+] = Ksp / [Cl-] = 1.7×10-10 / X
となる。仮に 0.1 mol / L の塩化物イオンを添加した場合には,溶液中に残存する銀イオン量は 1.7×10-9 × 107.87 g / L = 1.8×10-7 g / L = 0.18 ppm となるので,溶液中にこれより多くの銀イオンを含む場合には,固体の塩化銀を析出させられる。従って,沈殿物の回収と質量測定を適切に行うことで,ppm オーダー( 10-6 g / L )の銀イオン分析に適用できることが分かる。
このように,一般的な沈殿反応では,難溶性の塩を形成できる試薬を過剰量添加することで実施される。
溶液中に他のイオンを多量に含む場合
溶液中に沈殿反応と関係ない他のイオンを多量に含む場合は,イオン強度を考慮する必要が生じる。すなわち,イオン濃度ではなく,イオン強度から求めた活量係数を乗じたイオン活量で計算する必要がある。
イオンを多量に含む場合は,溶液のイオン強度を求め,イオン強度の範囲により活量係数を求めるのが一般的である。
溶液に含まれるイオンの電荷を Z1 ,Z2 ,Z3 ,・・・,モル濃度を C1 ,C2 ,C3 ,・・・とした時,溶液のイオン強度 I は,
I = 1 / 2 ( Z12 C1 + Z22 C2 + Z32 C3 + ・・・)
で与えられる。i イオンの活量係数γi の計算は,溶液のイオン強度 I の大きさにより次で求められる。
I ≦ 0.02
-log γi = 0.5 Zi2 √I
0.02 < I < 0.2
-log γi = 0.5 Zi2 √I / ( 1 + √I )
0.2 以上の濃厚溶液
濃厚溶液では,イオン毎の補正項が必要になる。
従って,イオン活量{ i }は,イオン強度から求めた活量係数γi とイオン濃度 [ i ] の積として扱わなければならない。上記の例では,
{ Ag+ } = γAg [ Ag+ ] ,Ksp /{ Cl-}= Ksp /γCl [Cl-]
となる。すなわち,沈澱分析に関わらないイオンを多く含むことで,分析できる濃度範囲が狭くなることを意味する。また,上述の銀イオン溶液に他のイオンとして 0.2 mol / L の硝酸( HNO3 )を含む場合はγAg = 0.6 , 0.2 mol / L の硫酸( H2SO4 )を含む場合ではγAg = 0.3 となり,イオン種により活量係数が大きく異なる。
| 物質名 | 溶解度積 | Ksp 値 | 物質名 | 溶解度積 | Ksp 値 |
|---|---|---|---|---|---|
| 塩化銀( AgCl ) | [Ag+] [Cl-] | 1.7×10-10 | 臭化銀( AgBr ) | [Ag+] [Br-] | 4.3×10-13 |
| 硫酸カルシウム( CaSO4 ) | [Ca2+] [SO42-] | 4.1×10-5 | 硫酸バリウム( BaSO4 ) | [Ba2+] [SO42-] | 1.7×10-10 |
| 炭酸カルシウム( CaCO3 ) | [Ca2+] [CO32-] | 4.96×10-9 | 炭酸バリウム( BaCO3 ) | [Ba2+] [CO32-] | 2.58×10-9 |
| 水酸化鉄(Ⅱ)Fe(OH)2 | [Fe2+] [ OH-]2 | 4.87×10-17 | 水酸化鉄(Ⅲ)Fe(OH)3 | [Fe3+] [ OH-]3 | 2.64×10-39 |
| 硫化鉄(Ⅱ)FeS | [Fe2+] [ S2-] | 1.59×10-19 | 硫化銅(CuS) | [Cu2+] [ S2-] | 1.27×10-36 |
| 硫化水銀(HgS) | [Hg2+] [ S2-] | 3.0×10-52 | 硫化亜鉛(ZnS) | [Zn2+] [ S2-] | 2.9×10-25 |
【参考】
活量係数( activity coefficient )
活量は,ギルバート・ニュートン・ルイスによって導入された物理量で,a で表される。活動度と呼ばれる場合もある。
反応の平衡や速度を議論するときに使われる濃度の有効値を指す。 また,理想とする数値からのずれを表す指標として,活量係数γが定義される。I 成分の活量 ai と理論上のモル分率χi の間には次の関係にある。
a i = γi χi
JIS K 0213 「分析化学用語(電気化学部門)」では,活量係数を次のように定義している。
aB / XB aB / ( mB / M0 ) 又は aB / ( CB / C0 ) で定義される数値。
ここに,aB :成分 B の相対活量, XB ,mB ,及び CB:それぞれ成分 B のモル分率,質量モル濃度,及びモル濃度, M0 ,及び C0 :それぞれ標準質量モル濃度(通常,1 mol / kg )及び標準モル濃度(通常,1 mol / L )
ページの先頭へ