第一部:化学と物質構造・共有結合
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,共有結合の特徴である【多重結合とは】, 【多重結合と電子雲の重なり】 に項目を分けて紹介する。
多重結合とは
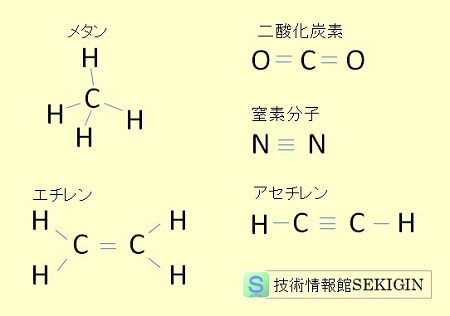
単結合,多重結合の構造式例
共有結合には,単結合の他に,2つの原子間で複数の電子対を共有する多重結合(二重結合,三重結合)を持つ化合物も多い。
例えば,二重結合の例としては,二酸化炭素( CO2 )の炭素原子・酸素原子間,エチレン( C2H4 )などの不飽和炭化水素の炭素原子間が,三重結合の例には窒素分子( N2 )の窒素原子間,アセチレン( C2H2 )の炭素原子間などがある。炭素・炭素間の多重結合は,有機化合物の合成や特性に大きく寄与することが知れてている。
結合の表示法
多重結合を持つ化合物の表示には,構造式を用いるのが一般的である。すなわち,一組の共有電子対を 1本の線で表す価標の本数で示す。例えば,窒素分子( N2 )を構造式で表すと( N ≡ N )となる。
【参考】
化合物の表示方法
分子構造の詳細をどの程度まで表現するかで,組成式( empirical formula ),分子式( molecular formula ),示性式( rational formula ),構造式( structural formula ),電子式( electronic formula )を使い分ける。
分子式: 分子に含まれる原子とその個数を的確に示す場合に用いるが,分子の一部が化学特性に大きく関わる場合には,示性式や構造式による表記が望ましい。
示性式: 構造が単純で構造的な紛らわしさが無い場合に,官能基などの結合関係を示す。
構造式: 共有電子対を価標(bond :線の数で単結合,二重結合,三重結合を表現する)で表示する。
電子式(ルイス構造式): ラジカル反応などの化学反応での電子のやり取りなどを特に示したい場合などに,共有電子対をコロン(単結合 :,二重結合 :: ,三重結合 ::: )で表示する。
ページのトップへ
多重結合と電子雲の重なり
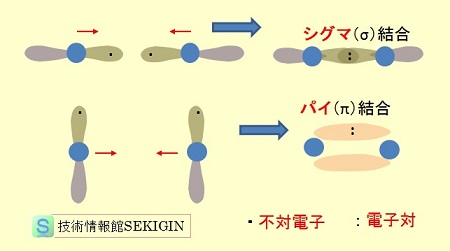
多重結合の電子雲
炭素・炭素間の多重結合では,電子軌道の重なり方が異なる混成軌道が形成される。
単結合では,下図に示すように,両原子の電子軌道の一つが縦方向に重なることで生じる。
一方,多重結合では,電子軌道の一つが縦方向で重なり,他の軌道の一つ又は二つが側面(横方向)で重なる。多重結合における縦方向の重なりをシグマ(σ)結合といい,横方向の重なりをパイ(π)結合という。
すなわち,炭素・炭素の二重結合はσ結合とπ結合を持つ sp2 混成軌道になり,三重結合は 1つのσ結合と 2つのπ結合を持つ sp 混成軌道になる。
【参考】
シグマ(σ)結合( σ-bond )
2原子間に形成される結合の対称性から名づけた名称の一つで,結合軸の方向の角運動量(angular momentum)成分を持たない,すなわち角運動量成分の量子数が 0の分子軌道関数(形は結合軸に対して対称)を表すσの軌道(σ軌道)に原子価電子が配置される結合をσ結合といい,σ結合を形成する電子をσ電子(σ-electron )という。σ電子は,2原子の s電子どうし,又は sと p電子である。
なお,角運動量成分の量子数 0,1,2,…に対して,分子軌道はσ,π,δ…などの記号で表す。
パイ(π)結合( π-bond )
2原子間に形成される結合の対称性から名づけた名称の一つで,結合軸のまわりの角運動量成分の量子数が 1である軌道(π軌道)に電子が配置される結合をπ結合という。π結合を形成する電子をπ電子( π-electron )という。
π軌道は,結合軸に垂直な p原子軌道どうしの重なりにより生じる。すなわち,π結合に関わる電子は,結合軸を x軸にとるとき,py‐py電子,pz‐pz電子である。
π軌道を形成する p原子軌道をもった多くの原子が,鎖状または環状の分子をつくるときは,π電子はπ軌道を通して原子から原子へと動くことができる(可動電子)。
運動量( momentum )
物体の運動の激しさを示すベクトル(運動方向を含む)量で,複数の物体の全運動量はベクトル和で表される。運動量には,並進運動で扱われる線運動量,回転運動で扱われる角運動量がある。
ページの先頭へ