物理 第二部:古典力学の基礎
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,生活に身近な円運動に関連し, 【円運動とは】, 【等速円運動とは】, 【等速円運動の向心力,周期,角振動数】, 【剛体の運動】, 【慣性モーメント】, 【トルクと角運動量】, 【剛体の回転運動】 に項目を分けて紹介する。
【円運動とは】
円運動(circular motion)とは,物体の運動の向きと垂直な方向に働く力で起きる運動である。物体の回転運動などの曲線運動は,物体の運動方向と垂直方向に働く向心力(求心力)で起きる運動である。天体の運動などは,ある原点との距離で決まる中心力で説明される運動である。
向心力(centripetal force)
求心力ともいい,曲線軌道(円軌道など)で運動をしている物体に働く力で,力の方向は,物体の速度と垂直方向,すなわち物体の経路における瞬間的な接触円の中心を向いている。
例えば,向心力は,紐に付けた物体を回転させた時の紐の張力の水平成分に比例する力である。なお,【慣性力】で紹介したように,回転座標系から見た時の,反対方向に働く見かけの力を遠心力というが,慣性力であり向心力に対する反作用の力ではない。
円運動では,円の中心に向かって向心力が働き,運動の速度,物体の質量に比例し,円の半径に反比例する。
すなわち,向心力 F の大きさは,円軌道の半径 𝒓 ,物体の質量 m ,角速度ωとすると,
F = mω2𝒓
で与えられる。物体の速度の大きさ(速さ)を |ν| とすると,|ν| = 𝒓 |ω|の関係から ,
F = mν2/ 𝒓
と書き直せる。
中心力(central force)
向心力とは定義が異なり,原点(定点)と物体を結ぶ線に沿って,原点と物体との距離 𝒓 にのみ依存する力,運動する物体相互を結ぶ線に沿って,物体間の距離で一義的に決まる力で,万有引力やクーロン力などがこれに相当する。
なお,中心力を受けている質点は,定まった平面上を運動し,力の中心に関する角運動量は変らない(ケプラーの法則)。
【参考:基礎用語】
- 作用・反作用の法則(law of action and reaction)
ニュートン力学の運動の第三法則で,“二つの質点 A , B の質点 A から質点 B に力(作用)を及ぼすと,同時に質点 B から質点 A に力(反作用)が及ぼされ,作用と反作用は大きさが等しく逆向きである”と定義されている。 - 角速度(angular velocity)
平面上を運動する点と原点を結ぶ線分(動径)が,原点を通る基線(定めた直線)となす角が,時間的に変化する割合(速さの程度)をいう。角速度は,原点を通り平面に垂直で,基線からこの動径の方向へまわした右ねじの進む向きのベクトルで表される。 - ケプラーの法則(Kepler's laws)
ヨハネス・ケプラーが発見し惑星の運動に関する法則。過去の観測記録などから太陽に対する火星の運動を定式化した次の 3 つの法則をいう。
第 1 法則(楕円軌道の法則:1609年):惑星は,太陽をひとつの焦点とする楕円軌道上を動く。
第 2 法則(面積速度一定の法則:1609年):惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である(面積速度一定)。
第 3 法則(調和の法則:1619年):惑星の公転周期の2乗は,軌道の長半径の3乗に比例する。 - 運動量(momentum)
物体の運動の激しさを示すベクトル量(運動方向を含む)で,複数の物体の全運動量はベクトル和で表される。
すなわち,質量 m の質点が速度 ν で運動している場合は,その積を運動量といい,ベクトル量 p = mν になる。なお,運動量の単位は,kg・m・s‐1 である。
円運動などでの角運動量と区別する場合は,線運動量ともいう。 - 速度(velocity)と速さ(speed)
速度とは,単位時間当たりの物体の位置の変化量である。日常用語として用いる速さとは,移動体が計測された時間間隔で進む距離である。
絶対値の単位は,速度,速さとも距離(m)÷時間(s) であるが,速度は移動方向を表すベクトル量で,速さは方向を含まないスカラー量である。
速度は,位置の変化量以外に,着目する現象の時間的に変化に対しても拡大使用され,面積速度,角速度,反応速度など,学術分野により種々の概念が定義されている。 - 面積速度(face velocity)
例えば,面積速度は,ケプラーの法則(Kepler's laws)の第2法則(面積速度一定の法則)で,惑星と太陽とを結ぶ線分が単位時間に描く面積と定義している。 - 角速度(angular velocity)
角速度は,質点は大きさを持たないが、一般の物体は大きさを持つため,回転運動が定義され,単位時間当たりの回転量と定義される。 - 反応速度(reaction rate)
反応速度は,化学反応の反応物あるいは生成物に関する各成分量の時間変化率と定義されている。
ページの先頭へ
【等速円運動とは】
等速円運動(uniform circular motion)とは,物体が半径 𝒓 の円周上を一定の速さ|ν|(スカラー量)で運動することである。
運動の向きは絶えず変化する。すなわち,速さは一定であっても,速度は絶えず変わるので,等速度運動ではない。
運動方程式を用いた説明
下図にあるように,x ,y 平面上で,原点 O を中心とし半径 𝒓 で円運動する物体の位置 P で,x 軸と動径 OP (原点と物体を結ぶ線分)のなす角をθ(ラジアン,rad )としたとき,物体の座標は,
x = 𝒓 cos θ
y = 𝒓 sin θ
で表される。
速度は,物体の位置の時間変化量なので,物体の位置を時間 t で微分すると,
![]()
となる。
dθ/ dt は,動径が向く角度の時間変化量で,角速度(angular velocity)という。
すなわち,角速度が一定な円運動が等速円運動となる。
等速円運動の角速度をω( rad/ s )で表し,dθ/ dt =ω を積分することで,
θ=ωt +α
が得られる。なお,αは積分定数で,初期条件で決まる初期位相といわれる。
等速円運動における物体の速度成分νx(= dx/ dt ),νy(= dy/ dt )は,
νx=‐𝒓ωsin ( ωt+α ),νy= 𝒓ωcos ( ωt+α )
で表される。
従って,速度νの大きさ,すなわち速さは,速度成分のベクトル和(ν2=νx2+νy2 )から,|ν|= 𝒓 |ω|で表される。
加速度は,速度の時間変化なので,速度成分の微分(位置の二階微分)から加速度成分は,
![]()
![]()
となる。
従って,加速度 a の大きさは,加速度成分のベクトル和から,| a |=ω2𝒓 で表される。
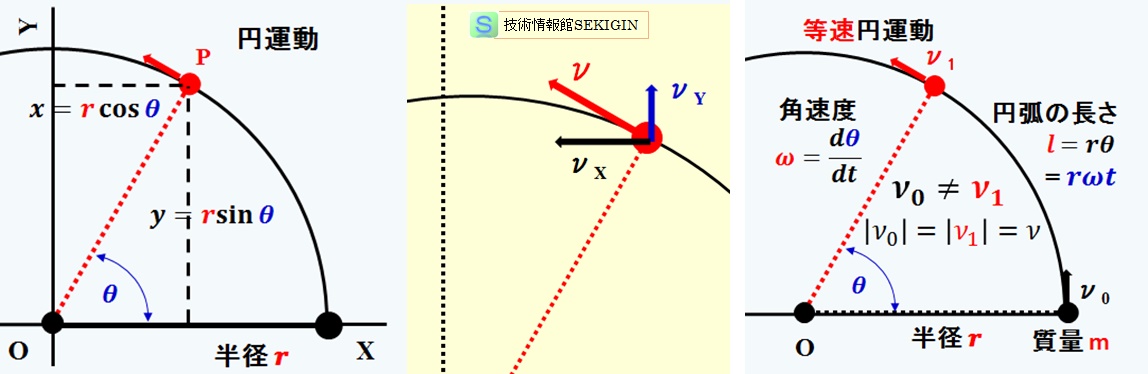
円運動
半径 r の円周上を物体が移動する等速円運動で,時間 t( s )で物体が移動した円弧の成す角をθ(ラジアン: rad )とし,円弧の長さ l (= 𝒓 θ)とすると,物体の速さ |ν|(m/ s )は,単位時間に物体の移動した距離なので,
|ν|= l / t = 𝒓 θ/ t
で求められる。
θ/ t は,単位時間当たりの回転角,すなわち角速度ω( rad/ s )なので,速さ |ν| は,
|ν| = 𝒓 |ω|
と表せる。
【参考:基礎用語】
- 等速度運動(motion of uniform velocity)
等速直線運動(uniform linear motion , linear uniform motion)の別称として用いられることが多く,物体が慣性の法則に従い直線上を一定速度で運動する。すなわち,初速度の大きさと方向が維持される。 - 位相(phase)
時間とともに周期的に変化する現象において,周期中の位置を示す量をいう。通常は角度(度やラジアン)で表される。例えば,正弦波で表される周期的な時間変化を y(t) = A sin(ωt + α) で表したとき,(ωt + α) を位相と言う。なお,t = 0 の位相( α )は特に初期位相と呼ばれる。
ページの先頭へ
【等速円運動の向心力,周期,角振動数】
向心力(centripetal force)
物体に働く力 F は,質量 m ,加速度 a とすると,ニュートンの運動の第二法則により
F= m a
で表される。
加速度のX軸成分とY軸成分の比は,
![]()
となり,加速度の向きが円の中心方向になることがわかる。
この円の中心方向への加速度は,向心加速度といわれ,物体に働く力は向心力といわれる。
向心力 F の大きさは,
| F | =m | a | = mω2𝒓
となる。
周期,角振動数(回転速度)
円軌道を一周するのに要する時間 T(s)を周期といい,一周( 2 π rad )を角速度ωで割った。
T = 2 π/ ω
で得られる。
周期の逆数は,単位時間当たりに円軌道を回転した数となるので,回転数( n ),角振動数( f ),回転速度などといわれる。なお,角振動数の単位は Hz (ヘルツ)である。
f = 1/ T =ω/ 2π
ページの先頭へ
【剛体の運動】
剛体(rigid body)とは,大きさを無視できない物体において,外からの力での変形(形や体積)が無視できると考えられる物体をいう。厳密にいうと,物体内のどの 2 点を取っても,その距離が不変なものといえる。
剛体の運動を考える際に,質点との相違に留意して考える必要がある。例えば,大きさを持つ剛体の全体の質量を代表する重心(center of gravity)がある。重心は,質量中心(center of mass)ともいわれ,重力場でその点を支点にしたとき,どの方向で支えてもうまく釣り合うような点である。
並進運動(translational motion)に関しては,重心に置かれた質点の運動に置き換えて考えることができる。回転運動(rotational motion)については,回転軸の方向によって,慣性モーメント(物体の回り難さの指標)が異なる。剛体の自由な回転運動では,重心を中心に回転していると考えることができる。
剛体の運動は,並進運動に関し,質量が重心に集中したと仮定したニュートンの運動方程式,回転運動に関し,重心のまわりの回転に関するオイラーの運動方程式を用いて理解される。
【参考:基礎用語】
- オイラーの運動方程式(Euler's equation of motion)
オイラーが導出した運動方程式で,ニュートンの運動法則を用いて導いた剛体の回転運動に関する方程式,粘性のない完全流体に関する運動方程式をいう。一般にオイラーの運動方程式という場合は,剛体の回転運動に関する方程式を指す場合が多く,これと区別するため流体の運動方程式はオイラーの流体運動方程式と呼ばれることが多い。 - オイラー(Leonhard Euler)
レオンハルト・オイラー(1707年~1783年)は,ロシア・ドイツの数学者・天文学者(天体物理学者)で,オイラーの公式,オイラーの等式,オイラー積分など,微分積分の創始以来で,解析学の技法的な完成に寄与した。 - 並進運動(translational motion)
物体のすべての点が平行移動する運動をいう。剛体の任意の運動は,重心とともに行う並進運動と重心のまわりの回転運動とに分解できる。 - 回転運動(rotational motion)
物体のすべての点が1つの固定点を中心とする同心球面上を同じ角速度で動く運動を,その固定点のまわりの回転運動という。 - 並進運動と回転運動関係
位置( 𝒓 )⇔ 角度(θ)
速度(ν= d𝒓/ dt )⇔ 角速度(ω= dθ/ dt)
加速度( 𝒂 = dν/ dt )⇔ 角加速度(α= dω/ dt )
質量( m )⇔ 慣性モーメント( 𝑰 )
運動量( p = mν)⇔ 角運動量( L = 𝒓 × p )
力( F )⇔ 力のモーメント(トルク)( N = 𝒓 × F )
ページの先頭へ
【慣性モーメント】
慣性モーメント(moment of inertia)は,慣性能率ともいわれ,回転運動において,並進運動における慣性質量(単位:kg )に対応する量で,回転運動を持続しようとする慣性の大きさを表わす量(記号 I ,単位:kg・m2 )である。
なお,モーメント(moment)とは,ベクトルで表される物理量とある原点に対する位置の外積をいう。
慣性モーメントは,物体を質量 dm の微小部分に分け,それぞれの微小部分から任意に定めた直線(三次元の座標軸や回転軸など)までの垂直距離 𝒓 としたとき,微小部分の質量と距離との自乗を物体全体について総和した量と定義される。
I=∑𝒓2dm
慣性モーメントは物体の質量や形状に依存するが,剛体では,物体の全質量 M とある長さ k を用いて,
I= M k2
で表わされることが多い。
ここで,長さ k は回転半径(radius of gyration)といわれ,物体の形と質量分布とによって決る値である。実用面から,簡単な形の均一物体の慣性モーメントや回転半径の値は数値表で与えられている。
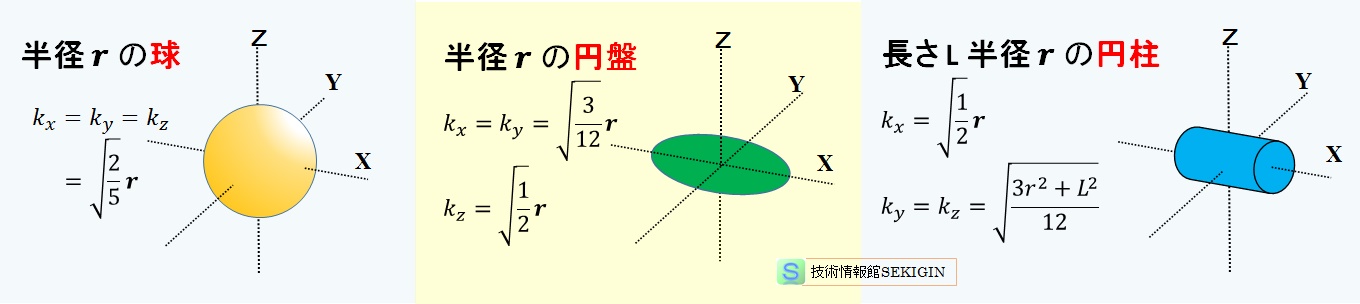
回転半径の例
- モーメント(moment)
モメントともいい,次の 3 つの意味で用いられる。
● 瞬間,非常に短い時間
● 契機,要因,きっかけ
● 物理用語で,能率と訳され,ある点または軸のまわりに運動を引き起こす能力を表す。
定点からその量までの距離をその量に掛けたもの,力の回転の効果は力のモーメント,運動量の効果は運動量のモーメント(角運動量)などで表す。 - 作用点(point of action)
物体内の力の働く点を作用点といい,作用点を通り力の方向に引いた直線を作用線(line of action)という。
剛体では作用点を作用線上のどこへ移しても力の効果は変わらない。 - 運動量(momentum)
物体の運動の激しさを示すベクトル量(運動方向を含む)で,複数の物体の全運動量はベクトル和で表される。
すなわち,質量 m の質点が速度 ν で運動している場合は,その積を運動量といい,ベクトル量 p = mν になる。なお,運動量の単位は,kg・m・s‐1 である。
円運動などでの角運動量と区別する場合は,線運動量ともいう。 - 三角関数
三角関数の微分
dsinθ/dθ = cosθ ,d2sinθ/dθ2 = - sinθ
dcosθ/dθ= - sinθ,d2cosθ/dθ2 = - cosθ
ピタゴラスの定理
sin2θ+ cos2θ = 1
ページの先頭へ
【トルクと角運動量】
質点に作用する力は,力の大きさと方向で表現できる。大きさを持つ物体に作用する力は,これらに加えて,力の作用点(point of action)が必要となる。
作用点を通り力の方向に引いた直線を作用線(line of action)という。変形しない剛体の場合は,作用線上のどこへ作用点を移動しても力が及ぼす効果は変わらない。
剛体における釣り合いを扱う場合は,力の釣り合いとともに,力のモーメントの釣り合いの条件が必要となる。
力のモーメント(moment of force)とは,力の能率ともいい,物体に回転を生じさせる力の効果の大きさを表す量で,その点から力の作用線までの距離(ベクトル)と力(ベクトル)の積(外積)で表され,単位にはニュートンメートル(N m := kg・m2・s‐2 )が用いられる。
固定された回転軸を中心に働く軸のまわりの力のモーメントをトルク(torque)やねじりモーメントと呼ぶ。
トルク N は,物体の作用点に加わる力 F ,回転軸から作用点までの距離 𝒓 とすると,ベクトル積(外積)の
N = r × F
で定義される。
角運動量(angular momentum)
運動量(momentum)とは,物体の運動の激しさを示すベクトル(運動方向を含む)量で,複数の物体の全運動量はベクトル和で表される。
運動量には,並進運動で扱われる線運動量,回転運動で扱われる角運動量がある。
単に運動量という場合には,線運動量を意味する。なお,線運動量( mν)は記号 P で表されるが,角運動量の記号には L が用いられる。
角運動量 L とは,運動量のモーメントを表す力学の概念で,位置ベクトル r と運動量 p の外積で定義される。
L= r × p
位置ベクトル r と運動量 p の成す角度θとすると,角運動量の大きさは,
| L | = | r |・| p | sin θ
で与えられる。
ある質点の質量 m ,速度 ν の時,運動量は p = mν で与えられるので,角運動量は,
L= r × mν= m r×ν
で表される。
ここで,角速度 ω とすると,
ν= r ω
ある質点の慣性モーメント I ,
I = r2m
とできる。
従って,角運動量 L は,慣性モーメント I と角速度ωを用いて
L= I ω
で表すことができる。
ページの先頭へ
【剛体の回転運動】
剛体(rigid body)とは,大きさを無視できない物体において,外からの力での変形(形や体積)が無視できると考えられる物体をいう。厳密にいうと,物体内のどの 2 点を取っても,その距離が不変なものといえる。
多くの固体は,力を加えられると多少なりとも変形するが,実用上で剛体として扱って不都合ない物が多い。
剛体の運動を考える際に,質点との相違に留意して考える必要がある。例えば,大きさを持つ剛体の全体の質量を代表する重心(center of gravity)がある。重心は,質量中心(center of mass)ともいわれ,重力場でその点を支点にしたとき,どの方向で支えてもうまく釣り合うような点である。
並進運動に関しては,重心に置かれた質点の運動に置き換えて考えることができる。
この時,剛体(質量 M )の重心の位置 S ,剛体に加わる全外力 F (=∑Fi )を用いることで,剛体の運動は,重心のニュートンの運動方程式として表示できる。
M d2S/ dt2 = F
回転運動(rotational motion)
回転軸の方向によって,慣性モーメント(物体の回り難さの指標)が異なる。剛体の自由な回転運動では,重心まわりの回転に関するオイラーの運動方程式で記述できる。
角運動量は,ニュートンの運動方程式と同様の関係にある。例えば,線運動量 p の時間的変化の割合に関する関係は,
dp/ dt = F
となる。
同様に,代表点を中心とした回転の角運動量 L ,外力による力のモーメント(トルク)の総和 N(= ∑(𝒓i×Fi) )の時,質点の角運動量の時間的変化の割合は,
dL/ dt = N
となる(オイラーの運動方程式)。
また,慣性モーメント I,角加速度 α(= dω/ dt )ともニュートンの運動方程式とよく似た関係が成り立つ。
dL/ dt = I ・dω/ dt = I α= N
回転エネルギー(rotational energy)
回転エネルギーとは,回転する物体がもつ運動エネルギー K で,回転が静止するまでに他に成す仕事となり,慣性モーメント I ,と角速度 ω の二乗に比例する。
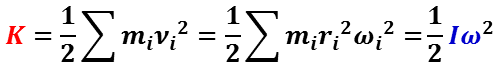
ページの先頭へ