第一部:化学と物質構造・共有結合
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎化学(目次)“ ⇒
ここでは,共有結合における【分子軌道について】, 【二原子分子の分子軌道】 に項目を分けて紹介する。
分子軌道について
【原子の構造】,及び【イオン結合】で扱った電子の軌道は,一つの原子核との相互作用を持つ原子価結合論(原子軌道)に基づくものである。
単原子分子(希ガス)を除き,複数の原子で分子を構成した場合には,結合に関与した電子は,原子間距離に応じて,一つ以上の原子核と相互作用をもつ分子軌道( molecular orbital )で記述される。
分子軌道の電子は,それぞれが固有のエネルギー状態を持ち,原子軌道の場合と同じ規則に従って,分子軌道を占めてゆく。
すなわち,電子はエネルギー準位の低い軌道から順番に満たされる。この際に,同じエネルギー準位の軌道(原子軌道では,同じ主量子数)では,各軌道にまず一個の電子が入り,空の軌道が無くなるとパウリの排他原理に従い,スピン量子数の異なる第二の電子が軌道を満たし始める。
量子化学において,分子軌道法( Molecular Orbital method ,通称 MO 法)は,原子に対する原子軌道の考え方を,そのまま分子に対して適用したもので,原子軌道の線形結合(量子力学的重ね合わせ)によって電子の波動関数を記述し,その電子状態(分子軌道)を求める計算手法を用いて記述される。
この手法を,LCAO 法( Linear combination of atomic orbitals method )あるいは原子軌道による線形結合法という。
平たくいうと,分子軌道法では,分子中の電子は,原子核や他の電子との相互作用を受けながら分子中を動き回ると考えて電子の挙動を解析している。
【参考】
分子軌道( molecular orbital )
単原子分子(希ガス)を除き,複数の原子で分子を構成した場合には,結合に関与した電子は,原子間距離に応じて,一つ以上の原子核と相互作用をもつ分子軌道で記述される。
エネルギー準位( energy level )
量子力学によれば,複数の粒子が引力によって結合している系(分子,原子,原子核など)のエネルギーは,一連のとびとびの値をとる。これを水準の高低になぞらえてエネルギー準位という。各エネルギー準位には一つまたは何個かの定常状態が対応する。複数の状態が対応するとき,準位が縮退(degeneration)しているという。定常状態を単にエネルギー準位という場合もある。最低のエネルギー準位に対応する状態を基底状態,それより高いエネルギーの状態を励起状態という。(世界大百科事典)
パウリの排他原理( Pauli principle )
パウリにより提唱された原理で,排他律あるいは禁制原理などとも呼ばれる。「 2つ以上のフェルミ粒子は,同一の量子状態を占めることはできない。」と表現され,一つの原子内では,2 個以上の電子が同時にエネルギー・スピンなどの同じ状態をとることはないことを示す原理である。
ページのトップへ
二原子分子の分子軌道
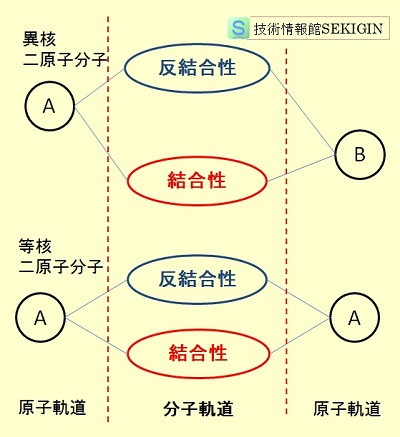
二原子分子の分子軌道
二原子分子( 2個の原子で構成する分子)では,結合に関わる電子が二つの原子核の影響を受け,結果として電子軌道が 2つに分裂する。
分子軌道法では,軌道は,原子それぞれの軌道の波動関数の和と波動関数の差になる。原子 Aの波動関数をψA,原子 Bの波動関数をψBとすると,分子 ABの波動関数は,和分のψMOⅠ,差分のψMOⅡになる。
すなわち,
ψMOⅠ= a ψA+ b ψB
ψMOⅡ= c ψA- d ψB
ここで a ,b ,c ,d は,原子の組み合わせなどで決まる因子( weighting factor )である。
MOⅠは2つの原子間の電子密度が高く,結合性分子軌道( bonding molecular orbital )という。
MOⅡは電荷の密度が極めて低く,反結合性分子軌道( antibonding molecular orbital )と呼ばれ,結合性分子軌道よりエネルギー順位が高い。
いずれの分子軌道もσ結合,π結合のいずれにもなれる。
右図には,等核二原子分子と異核二原子分子の場合の分子軌道を模式的に示した。
等核二原子分子,異核二原子分子のいずれの場合も,元の原子軌道よりエネルギーの低い分子軌道(結合性)とエネルギーの高い分子軌道(反結合性)に分裂する。
従って,両原子の不対電子は,結合により,エネルギーの低い結合性分子軌道の共有電子対となることができる。
【参考】
分子軌道法に関するネット情報例:「混成軌道と多重結合、分子軌道法」, 「フラグメント分子軌道法の基礎」, 「分子軌道法を学ぶために - 京都大学」, 「2.分子軌道法解説」など
ページの先頭へ