物理 第五部：熱力学

　温度が上昇すると物質の大きさ（長さ，体積）が変わる現象は，日常生活の中でも多く経験される。これを熱膨張（thermal expansion）という。
　気体の熱膨張については，気体の状態方程式として別途で紹介している。ここでは，主に固体の熱膨張について紹介する。
　
　固体の長さの変化（増加）は線膨張（linear expansion），体積の変化（増加）は体膨張（cubical expansion , volume expansion）と呼ばれる。
　物体の熱膨張のし易さの程度を表わす係数を熱膨張係数（coefficient of thermal expansion ，熱膨張係数ともいう）といい，単位は熱力学的温度の逆数の K^-1 である。
　熱膨張係数も，長さの変化し易さの指標となる線熱膨張係数（coefficient of linear thermal expansion），体積の変化し易さの指標となる体膨張係数（coefficient of volume expansion）に分けられる。
　
　線熱膨張係数と体膨張係数の関係
　氷のように，温度により分子の配列が変わるような特殊な物質を除き，一般的な固体では，比較的広い温度範囲で膨張係数の変化が小さい。
　線熱膨張係数 α は，ある温度 t₀ での長さを l ₀とした時，温度 t = t₀ + dt で長さ l = l₀ + dl になったとすると，
　　　　　　　
で与えられる。
　体膨張係数 γ は，線熱膨張係数と同様にして，
　　　　　　　
で与えられる。
　ここで，固体を，一辺の長さ l ₀ の立方体とすると，
　　　　　　　
が得られ，多くの固体の体膨張係数は，線熱膨張係数の 3 倍となる。
　なお，実用される物質では，固体・液体の熱膨張は物質の混合等によるものも含め，下記の例に示す水のように相の違いにより大きく変わるので，温度などの条件が異なる場合の物質間の大小関係は不定である。
　
　一般的な物質（固体）と水の線熱膨張係数（ 25℃：× 10^-6 K^-1 ）
　金属
　鉄（11.8），亜鉛（30.2），アルミニウム（23.1），銅（16.5），チタン（8.6）
　無機物
　ダイヤモンド（0.8），けい素（2.6），岩石（5 ～ 8 ），石英ガラス（～ 0.5）
　有機高分子化合物（品質により範囲が広い）
　ナイロン（60～100），ポリカーボネート（50～70），ポリエチレン（120～200），ポリ塩化ビニル（60～80），エポキシ樹脂（40～80），ふっ素樹脂（45～70），シリコーン樹脂（250～300）
　水（体膨張係数）
　25℃（210）， 4℃（0），4～0℃（負），水 0℃（‐60），氷 0℃（52.7），- 50℃（45.6）
　
　【参考：基礎用語】

• 固体（solid）
  　液体と比較して変形や体積変化が極めて小さい。固体を構成する粒子（原子，分子やイオン）は，粒子間の相互作用（引力）により粒子（原子や分子）の位置がほぼ固定され，移動が制限される。粒子が規則正しい繰り返しで並ぶ場合（結晶）と不規則に並ぶ場合（アモルファス）がある。
• 液体（liquid）
  　流動的で容器に合わせて形を変えることができる。液体は気体と異なり，粒子間の相互作用（引力）が比較的弱く，粒子（原子や分子）の位置は固定されず，自由に流動できるが，粒子間の距離がほぼ一定に保たれるため容器全体に広がることが無い。また，圧縮性が小さいので，ほぼ一定の密度を保つ。一般的に，液体の密度は，固体の密度に近く，気体より著しく高い。
• 気体（gas）
  　一定の形と体積を持たず，自由に流動し，圧縮やずれに対する抵抗が小さく，圧力の増減で体積が容易に変化する状態である。また，外部から力を受けない状態では，気体の体積が無限に膨張する。
  　気体を構成する粒子（原子や分子）は，自由かつランダムに動く熱運動をしている。気体の粒子は，それぞれ離れているため，粒子間には引力（分子間力）が働かない。
• 相（phase）
  　境界面で空間的に区別された均質な部分を相と呼ぶ。例えば，固相，液相，気相と呼ぶが，同じ物質の固相でも結晶構造が異なれば，ほかの相とみなされる。
  　1 相だけの物質を均一系または単相系，2 相以上からできている物質を不均一系または多相系という。
• 熱膨張（thermal expansion）
  　JIS K6900（プラスチック用語）では，“温度の変化による試験片の寸法又は体積の変化。”と定義されている。
• 線膨張（linear expansion）
  　JIS K6900（プラスチック用語）では，“特定の試験条件のもとでの試験片の寸法変化。体膨張，膨潤及び線熱膨張係数も参照。”と定義されている。
• 体膨張（volume expansion）
  　JIS K6900（プラスチック用語）では，“特定の試験条件のもとでの試験片の体積変化。線膨張及び膨潤も参照。”と定義されている。
• 膨潤（swelling）
  　JIS K6900（プラスチック用語）では，“液体の中に浸せきされ又は蒸気にさらされた試験片の体積の増大。”と定義されている。
• 線熱膨張係数（coefficient of linear e thermal xpansion）
  　JIS K6900（プラスチック用語）では，“温度変化 1 度当たりの単位長さ当たりの材料の長さの可逆的な変化。IUPAP 記号 α 。注：その値は異なる温度範囲の場合に変化することもある。”と定義されている。
  　一般には，線熱膨張係数と呼ぶことも多いが，熱による膨張の場合は厳密には線熱膨張係数と呼ぶのが望ましい。
• 体膨張係数（coefficient of volume expansion）
  　物体の温度を 1 度上げたときの体積の増加量ともとの体積との比。

　熱容量（heat capacity）は，限定された範囲であるが，熱を保存されるもののように考えることで，自然現象の説明を容易にするために導入された概念である。
　熱容量は，系に対して熱の出入りがあったとき，系の温度がどの程度変化するかを表す系固有の状態量で，記号 C ，単位 J･K^‐1 （ジュール毎ケルビン）が用いられる。
　従って，熱容量 C は，熱量 ∂Q を得た時の温度変化 dT に相当するので，
　　　　　　　
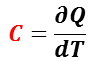
で与えられる。
　
　熱容量は，系の熱の出入りなので，系の質量に比例するため，物質間の比較が困難である。
　そこで，単位質量当たりの熱容量，すなわち，質量 1 kg の物質を 1 K（＝ 1 ℃）上昇させるのに必要な熱容量を示す，その物質の比熱容量（specific heat capacity）が用いられる。従って，熱容量 C は，質量 m と比熱容量 c との積，
　　　　　　　C = mc
で与えられる。
　
　比熱容量は，単に比熱とも呼ばれ，単位は J･kg^‐1･K^‐1 である。なお，一般的には，温度によって変化するので，
　比熱容量を表示する場合は，温度の指定が必要である。
　原子量，分子量（モル）当たりの熱容量を原子熱（比熱容量×原子量），分子熱（比熱容量×分子量）という。分子熱は，モル比熱，モル熱容量とも呼ばれる。
　
　液体や固体の体積は，温度による極端な変化はないが，気体は，温度によるエンタルピーや
　体積の変化が大きいため，圧力を一定に保ちながら測定した値と体積を一定に保ちながら測定した値で大きな違いがでる。
　前者を定圧比熱容量（specific heat capacity at constant pressure），後者を定積比熱容量（specific heat capacity at constant volume）や定容比熱容量といわれている。
　
　比熱容量の一般的特徴
　圧力一定で温度を上げると，一般には体積が増加し，その分の熱を必要とするため，一般的な物質では，定圧比熱容量＞定積比熱容量である。気体（理想気体）の場合は，後述するマイヤーの関係式が成立する。
　気体の混合物については，一般的には，モル分圧比が成り立つ。
　デバイ温度より大きい領域の単体の固体では，定積モル熱容量が一定（デュロン＝プティの法則）になる。
　　　　定積モル熱容量＝ 3 R = 3 N_A ･ k_B
　　　　ここで，R ：気体定数，N_A ：アヴォガドロ定数，k_B ：ボルツマン定数
　主な元素単体のデバイ温度：亜鉛（327 K = 53.85℃），銅（343.5 K = 70.35℃），アルミニウム（428 K = 154.85℃），鉄（470 K = 196.85℃）
　金属中の自由電子系の比熱容量（電子比熱）は，低温では絶対温度（熱力学(的)温度）に比例する。
　
　主な物質（固体）の比熱容量（J･kg^‐1･K^‐1）
　主な物質の比熱の例を次に示す。温度表示のない物は，標準状態（SATP： 25 ℃ 1 気圧 ）での値を示す。
　金属
　金（20℃，129），銅（385），鉄（444），アルミニウム（900）
　無機物
　ダイヤモンド（502），ガラス（677），氷（ 0℃，2 060，水 25℃，4186）
　有機高分子化合物（品質により範囲が広い）
　ナイロン（1 500～2 500），ポリカーボネート（1170～1260），ポリエチレン（1570～2300），ポリ塩化ビニル（920～1470），エポキシ樹脂（1050）
　
　【参考：基礎用語】

• 原子熱（atomic heat）
  　原子熱容量ともいい，原子量と比熱の積で表され，1 モルの物質の温度を 1K 上げるための熱量をいう。
• モル熱容量（molar heat capacity）
  　モル比熱，分子熱ともいい，単位 J・mol^-1 で，系の熱容量をその系の物質量（モル数）で割ったものである 。
• マイヤー（Julius Robert von Mayer）
  　ドイツの物理学者，ユリウス・ロベルト・フォン・マイヤー（1814年～1878年）は，熱と仕事が相互に変換可能であること，エネルギー保存の法則を発表。比熱に関するマイヤーの関係式でも知られる。
• デバイ温度（Debye temperature）
  　デバイの考案した固体におけるフォノンの比熱（熱容量）への寄与を推定する手法であるデバイモデル（Debye model）では，低温における比熱が熱力学的温度（絶対温度）の三乗（ T³ ） に比例（デバイのT3 法則）する。このデバイの T3 法則の成立する限界温度をデバイ温度（デバイの特性温度）という。
• デバイ（Peter Joseph William Debye）
  　ピーター・ヨセフ・ウィレム・デバイェ（1884年 ～ 1966年）は，オランダの物理学者・化学者で，デバイ温度，電気双極子モーメントの単位（デバイ），デバイモデル，デバイ-ヒュッケルの式などで知られる。
• デュロン＝プティの法則（Dulong-Petit law）
  　固体の定積モル比熱は，炭素，ホウ素などの少数の例外を除くと，ほとんど一定で約25J/deg（気体定数Rの約３倍）であるというデュロンPierre Louis Dulong(1785‐1838)とプティAlexis Thérèse Petit(1791‐1820)によって1819年に発見した経験法則。
• デュロン（Pierre Louis Dulong）
  　フランスの物理学者，化学者のピエール・ルイ・デュロン（1785年 ～ 1838年）は，比熱に関するデュロン＝プティの法則で知られる。
• プティ（Alexis Thérèse Petit）
  　フランスの実験物理学者のアレクシ・テレーズ・プティ（1791年 ～ 1820年）

　気体は，温度によるエンタルピーや体積の変化が大きいため，圧力を一定に保ちながら測定した定圧比熱容量（specific heat capacity at constant pressure）と体積を一定に保ちながら測定した定積比熱容量（specific heat capacity at constant volume）とで大きな違いがでる。
　
　熱力学第一法則で紹介するように，エネルギー移動の形態には，仕事と熱があり，ある系に成した仕事 𝜕 W ，系に与えた熱量 𝜕 Q としたとき，内部エネルギーの変化量 dU は，
　　　　　　　dU = 𝜕 Q + 𝜕 W
で与えられるので，熱量の変化は，
　　　　　　　𝜕 Q = dU ‐𝜕 W
と書ける。
　
　圧力 p 一定の条件で，熱 𝜕 Q を受けたある系が，準静的な過程を経て，体積が dV だけ増加した時に，外界に対してする仕事は， 𝜕 W = ‐p dV となるので，熱量の変化は，
　　　　　　　𝜕 Q = dU ＋ p dV
となる。
　一方で，エンタルピーは，系の圧力 p ，体積 V と内部エネルギー U のとき，エンタルピー H は，
　　　　　　　　H ＝ U ＋ pV
と定義される。従って，エンタルピーの変化 dH は，
　　　　　　　　d H ＝ d ( U ＋ pV ) = d U ＋ p dV ＋V dp = 𝜕 Q ＋ V dp
となる。従って，
　　　　　　　　𝜕 Q ＝ d H － V dp
となる。
　
　以上より，圧力一定の場合の定圧熱容量（ C_p ）は，エンタルピー変化の式から
　　　　　　　
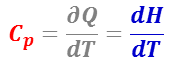
となり，体積一定の場合の定積熱容量（ C_V ）は，内部エネルギー変化の式から
　　　　　　　
　
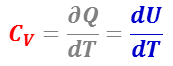
　【参考：基礎用語】

• エンタルピー（enthalpy）
  　熱含量（heat content）とも言われ，一般的には記号 H で表される。系の圧力 P ，体積 V と内部エネルギー U のとき，エンタルピーは，次のように定義される。
  　　　　　H ＝ U ＋ P V
• 熱力学第一法則（the first law of thermodynamics）
  　「孤立系のエネルギーの総量は変化しない。」という熱力学の基本法則の一つで，エネルギー保存の法則（ the law of the conservation of energy ）やエネルギー保存則とも呼ばれる。
• 内部エネルギー（internal energy）
  　系の総エネルギーから，系が全体としてもつ運動エネルギー，外力による位置エネルギーを引去った残りのエネルギーをいう。すなわち，物体内部の状態だけで決まるエネルギーをいう。
• 準静的（quasistatic process）
  　物質系の変化が熱力学的平衡に十分近い状態を保ちながら起こること。
• 熱力学的平衡（thermodynamic equilibrium）
  　熱力学的系が熱的，力学的，化学的に平衡，すなわち，巨視的状態量が一定の値を保つ，変化しない状態をいう。
• 理想気体（ideal gas）
  　理想気体は，完全気体（ perfect gas ）ともいい，現実には存在しない理想的な気体である。すなわち，ボイル＝シャルルの法則を状態方程式とし，内部エネルギーは体積によらず温度だけの関数となり，断熱変化に対してポアソンの法則に従う。
  　このためには，気体を構成する粒子（分子や原子など）の体積と，粒子間の相互作用をともに無視できる系として扱われる。
• 自由度（degree of freedom）
  　一般には，変数のうち独立に選べるものの数をいう。物理的には，ある運動状態や平衡状態を表すのに必要な任意に独立に変化させることができるものの数をいう。

　マイヤーの関係式とは
　圧力一定で温度を上げると，一般には体積が増加し，その分の熱を必要とするため，一般的な物質では，定圧熱容量＞定積熱容量である。
　理想気体の場合は，定積熱容量（ C_V ），定圧熱容量（ C_p ），気体定数（ R = 8.3144621(75) J･K^-1･mol^-1 ），物質量（n モル）に，
　　　　　　　C_p ＝ C_V ＋ nR
の関係があることを，ドイツの理学者ユリウス・ロベルト・フォン・マイヤー（1814 ～ 1878年）が発見したため，マイヤーの関係式（Meyer’s relation）といわれる。
　
　関係式の導出
　前述したエンタルピー（ H ），内部エネルギー変化（ U ），定圧熱容量（ C_p ）の関係式，
　　　　　　　d H ＝ d ( U ＋ pV ) = d U ＋ p dV ＋V dp = 𝜕 Q ＋ V dp
　　　　　　　
　　　　　　　
と，気体の状態方程式　pV = nRT　（n ：物質量モル，R ：気体定数，T ：熱力学(的)温度）とから，
　　　　　　　
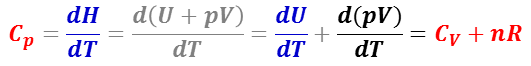
が得られる。

　比熱比（specific heat ratio , heat capacity ratio）とは，1 モル当たりの定圧比熱容量（ C_p ）と定積比熱容量（ C_V ）との比をいい，通常は記号γ（又はκ）を用いて，
　　　　　　　
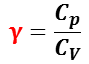
と表わす。
　
　比熱比と気体分子の自由度
　液体や固体の比熱比はγ≒ 1 であるが，気体分子の運動エネルギーに，分子の回転運動が含められるため，分子構造の違い（運動の自由度）が比熱比に影響する。
　理想気体における気体分子の運動の自由度 f と内部エネルギー（ U ），定積比熱容量（ C_V ），定圧比熱容量（ C_p ）との関係は，次の通りである。
　1 モルの気体分子は，1 自由度につき RT/ 2 の内部エネルギーを持つので，
　　　　　　　U = f×RT/ 2
となる。従って，上述の定積比熱容量と定圧比熱容量の定義により，
　　　　　　　C_V = f ×R/ 2
　　　　　　　C_p = C_V ＋ R = ( f＋2 )×R/ 2
とできるので，比熱比γは，
　　　　　　　γ＝ ( f＋2 )/ f
となります。
　
　分子種の自由度と比熱比
　気体分子の自由度の観点からは，He , Ar などの単原子分子，N₂ , O₂ などの 2 原子分子，CO₂ , NH₃ , CH₄ などの多原子分子に分けられる。
　単原子分子：自由度 f ＝ 3 （並進），γ≒ 5/ 3（1.67）
　2 原子分子：自由度 f ＝ 4（並進 3 ＋回転2 ），γ≒ 7/ 5（1.40）
　多原子分子： f＝ 6（並進 3 ＋回転 3 ），γ≒ 4/ 3（1.33）