物理 第一部:物理学とは
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,古典物理学(力と運動)の基本について,【ニュートンの運動の法則】,【慣性の法則】,【作用・反作用の法則】,【運動方程式】,【慣性質量と重力質量】に項目を分けて紹介する。
【ニュートンの運動の法則】
ニュートンの運動の法則(運動の第1法則,第2法則,第3法則),万有引力の法則(law of universal gravitation)など二体間に働く力を基礎とした力学体系で,古典力学(classical mechanics)ともいわれる。
運動の法則(law of motion)
物体を重心に全質量が集中し,大きさをもたない点(質点)と仮定し,次の 3 法則をいう。
質点とは,物体を重心に全質量が集中し大きさをもたない点と仮定したものである。
第1法則(慣性の法則:law of inertia)
外から力が作用しない限り,質点は静止または等速直線運動する。
第2法則(ニュートンの運動方程式:Newton's equation of motion)
質点の加速度 a は,そのとき質点に作用する力 F に比例し,比例定数 m に反比例する ma=F 。比例定数 m が質点の質量(慣性質量)である。
第3法則(作用・反作用の法則:law of action and reaction)
二つの質点 A , B の質点 A から質点 B に力(作用)を及ぼすと,同時に質点 B から質点 A に力(反作用)が及ぼされ,作用と反作用は大きさが等しく逆向きである。
【参考:基礎用語】
- 恒星系(star system , stellar system)
少数の恒星が重力で結びついてお互いの周りを公転している星系をいう。なお,数多くの恒星が密集して雲塊状になっているものを星団(star cluster)といい,太陽系を含む恒星の大集団を銀河系(galaxy)という。
恒星(fixed stars)とは,古典天文学で天球上に固定している星をいい,惑星と区別して呼ばれた。恒星は,太陽と同様に,自ら光を発し,その質量がもたらす重力による収縮に反する圧力を内部に持ち支えるガス体である。 - 太陽系(solar system)
一つの恒星(太陽)とその引力によって,太陽を中心に運行している天体の集団をいう。
太陽系を構成する天体は,大きさと運動の違いにより 8 個の惑星(水星・金星・地球・火星・木星・土星・天王星・海王星),惑星の衛星,準惑星(冥王星),太陽系小天体(小惑星・彗星や流星物質・ガス状の惑星間物質など)に分けられる。
なお,海王星の外を回る冥王星は,長く惑星とされていたが2006年に国際天文学連合により準惑星に分類された。 - 地球(earth)
太陽系の 3 番目の惑星で,表面に水,酸素を大量に蓄えた空気があり,多様な生物が生存することを特徴とする。
太陽からの平均距離 1 億 4960 万 km にあり,太陽を一つの焦点とする円に近い楕円軌道上を 365.2563 日の周期で公転し,公転軌道面と約 66.5 °の傾きを保つ地軸を軸として 23 時間 56 分 4.09 秒の周期で自転している。
地球の大きさは,赤道半径 6378.388 km ,極半径 6356.912 km ,全質量 5.973×1027g ,平均密度 5.52 g/cm3である。 - 力の単位 N(ニュートン)
質量 1 kg の質点に力を加えて,加速度 1 ms‐2 を得た時の力を 1 N(=1 kg・ms‐2 )と定義されるが,1948 年に国際単位系( SI 単位)に採用されるまでは,力の単位として重量キログラム( kgf:kilogram-force,又はkgw:kilogram-weight )が用いられていた。
1 kgf = 9.80619920 N(≒9.8 N )
重量キログラムは,加速度に重力を用い,地上では感覚的に,バネばかりなどによる重さ測定などの実用面でも受け入れやすい。このため,現在でもしばしば利用されている単位である。
ページの先頭へ
【慣性の法則】
慣性の法則(law of inertia)とは,ニュートン力学の運動の第一法則で,“物質の外から力が作用しない限り,質点は静止または等速直線運動する”と定義されている。
ここで,“物体の外から力が作用しない限り”を厳密に表現すると,物体に外から力が作用していない場合の他に,物体に作用している力が釣り合っている場合(力の和ベクトルがゼロ)を意味する。
日常の生活では,力が外から作用していない場合の慣性の法則は,これに近い現象の観察は可能であるが,実際には,摩擦力や抵抗力があり厳密な意味での慣性の法則は観察困難である。
摩擦力や抵抗力が殆ど無い宇宙空間であっても,惑星,恒星などとの引力の影響を受けている。
力が釣り合っている場合の慣性の法則は,限られた条件の下では観察可能である。
このため,慣性系(inertial system)という概念を導入し,慣性の法則は,次の様に表現される。
“静止している物体に力が働かないとき,その物体は慣性系に対し静止を続ける。運動する物体に力が働かないとき,その物体は慣性系に対し運動状態を変えず等速直線運動を続ける。”
慣性系は,慣性座標系(inertial frame of reference)ともいい,慣性の法則(運動の第1法則)が成立する座標系である。ある慣性系に対し等速度で並進運動する座標系も慣性系である。
恒星系に固定した座標系は近似的に慣性系であることが知られている。すなわち,恒星系に対して回転しない座標系は慣性系に近い。
恒星系(太陽系)に対し,地球は回転運動(慣性系に対し加速度運動)しているが,その運動と自転は穏やかなので,大規模な運動(台風など)や高速運動しない限り,地球の表面は近似的に慣性系として見なす事が出来るといわれている。
慣性の法則の説明に用いられる地表での現象例
地表に静止している物体は静止し続ける。地表に対して等速直線運動している物体 A(例えば車,エレベータ)の中で静止している物体 B は,物体 A に対して静止し続けるが,地表の観測者の座標からは,物体 A と共に等速直線運動し続ける。
ページの先頭へ
【作用・反作用の法則】
作用・反作用の法則(law of action and reaction)とは,ニュートン力学の運動の第三法則で,“二つの質点 A , B の質点 A から質点 B に力(作用)を及ぼすと,同時に質点 B から質点 A に力(反作用)が及ぼされ,作用と反作用は大きさが等しく逆向きである”と定義されている。
ここで留意すべきことは,作用と反作用の力の和ベクトルがゼロとなるが,関連する質点が二つ,すなわち,作用の力が及ぶ物質と反作用の力が及ぶ物質は異なることである。
一つの物質(質点が一つ)に,二つの力が作用し,その力が釣り合っている場合(力の和ベクトルがゼロ)は,この二つの力の関係を作用・反作用の力とは言わない。
例えば,下図のように,選手 A と選手 B の綱引きで,ホールド状態になった時を考える。ロープと選手の接点に注目すると,選手がロープを引く力を加えた時,この作用に対し,同時に同じ大きさで向きが反対のロープが選手を引く反作用が発生する。
一方,ロープのみに着目すると,ロープは両選手から同じ大きさで反対向きの 2 つの力が作用し,力の釣り合いの状態にある。
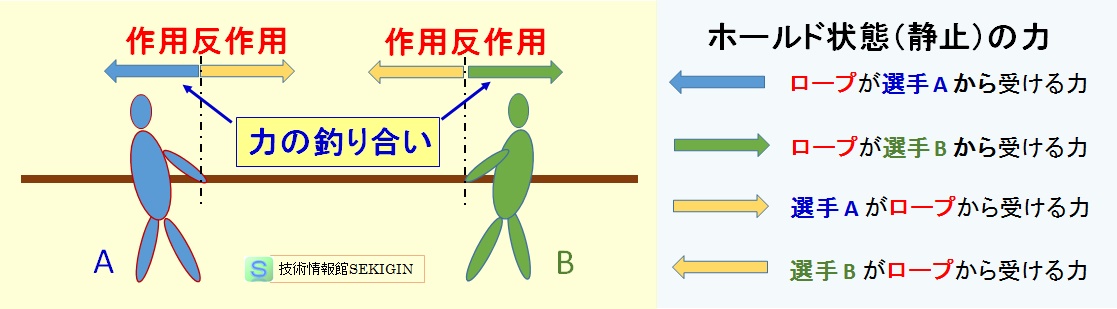
作用・反作用の法則と力の釣り合い
ページの先頭へ
【運動方程式】
ニュートンの運動方程式(Newton's equation of motion)とは,ニュートン力学の運動の第二法則で,“質点の加速度 a は,そのとき質点に作用する力 F に比例し,比例係数 m (質点の質量)に反比例し,ma=F で表される”と表現される。
質量 m の物体に一定の力![]() を加え続けると,力のベクトルの方向に物体は速度(
を加え続けると,力のベクトルの方向に物体は速度( ![]() )を増しつつ移動する。速度の時間変化を加速度(
)を増しつつ移動する。速度の時間変化を加速度(![]() )というが,加えた力と同じ方向を持つベクトル量である。
)というが,加えた力と同じ方向を持つベクトル量である。
加速度は,力と比例関係にあり,
![]() =
=![]()
で表される。この式を運動方程式といい,比例定数 m は物体の動かし難さの度合いを表し,ニュートン力学では,慣性質量(inertial mass)と定義される。なお,単に質量という場合は,慣性質量を示すのが一般的である。
力の単位 N(ニュートン)は,質量 1 kg の質点に力を加えて,加速度 1 ms‐2 を得た時の力を 1 N(=1 kg・ms‐2 )と定義される。
ページの先頭へ
【慣性質量と重力質量】
重力質量(gravitational mass)とは,万有引力の法則(law of universal gravitation)により導かれる質量の概念で,運動の法則から導かれるa href="phys_01_00.html" target="_blank">慣性質量とは定義が異なる。
重力質量 mG は,地球上の物体に作用する地球の万有引力を意味する重力(gravity)を起こす質量で,重力 FG とその場所での重力加速度 g (9.80619920 ms‐2 ≒ 9.8 N/kg)により,
FG=mG g
で表され,直感的にイメージする「重さ」を生じさせる質量である。なお,慣性質量と重力質量は,定義が異なるにもかかわらず,同一の値をとる。この経験則を等価原理というが,同じ値をとる理由は明確になっていない。
ページの先頭へ