物理 第四部:波・波動の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,最も身近な光(電磁波)の波動としての特性に注目した物理光学に関し, 【物理(波動)光学とは】, 【干渉とは】, 【反射で位相が変化する干渉の例】, 【回折とは】, 【偏光とは】, 【ブルースターの法則】, 【複屈折現象】 に項目を分けて紹介する。
【物理(波動)光学とは】
物理光学(physical optics)は,波動光学ともいう光学の一部門で,幾何光学に対して用いられる。
18 世紀にイギリスの物理学者ヤングやフランスの物理学者フレネルが,17 世紀(1600 年代)に行われていた光に関する観察や実験結果に対し,波動としての性質による結果であることを明らかにしたことから,波動光学(物理光学)が発達した。
物理光学では,光の波動性に着目した光波という概念で捕え,波動に伴う特有な現象である干渉,回折,偏光,分散,散乱,放射,吸収など光と物質との相互作用などを論じる分野である。
それぞれ用語の定義を JIS Z 8120 「光学用語」より抜粋して示す。
干渉(interference)
二つ以上の光波が同一点で重なりあって互いに強め合い,又は弱め合う現象。
回折(diffraction)
a) 光が物体に当たったとき,直進せずに広がって進み,物体の影の部分にも光が回りこむ現象。
b) 強度が断面内で一様でない光束において,光線が直進せずに広がって進む現象。
偏光(polarized light)
光波(電気ベクトル)の振動方向が規則的な光。 直線偏光,円偏光,だ円偏光がある。
分散(dispersion)
a) 光が物質の中を伝搬する場合,光学的性質が波長によって異なる現象。
b) 媒質の屈折率が放射の単色光成分の周波数に応じて異なる現象。
散乱(scattering ,拡散:diffusion)
光が極めて小さい凹凸のある反射面に入射する場合,又は極めて小さい粒子を含む媒質の中を通過する場合に,光の進行方向が空間的に多くの方向に変わる現象。
放射(radiation)
a) 電磁波(又は光子)によるエネルギーの放出又は伝搬。
b) これらの電磁波(又は光子)。
吸収(absorption )
放射エネルギーが物質との相互作用によって他の種類のエネルギーに変換する現象。
【参考:基礎用語】
- ヤング(Thomas Young)
トマス・ヤング(1773年 ~ 1829年)は,イギリスの物理学者,医師で,医学の分野で乱視,色の知覚(ヤング=ヘルムホルツの三色説)などの業績を残し,物理の分野では,光の干渉現象(ヤングの実験),光の波動説,ヤング率(弾性体力学)に名前を残などの業績を残す。 - フレネル(Augustin Jean Fresnel)
オーギュスタン・ジャン・フレネル(1788年~1827年)は,フランスの物理学者,土木技術者,光の波動説を唱え,光の回折や複屈折現象などの理論研究,灯台や投光器に用いるフレネルレンズの発明など光学分野で業績を残す。
ページの先頭へ
【干渉とは】
JIS Z 8120 「光学用語」では,干渉(interference)を “二つ以上の光波が同一点で重なりあって互いに強め合い,又は弱め合う現象”と定義されている。
すなわち,媒質中を同時に2つ以上の波が伝わるとき,各点での波の振幅が,単振動合成で紹介した重ね合わせの原理に基づく合成波になる現象である。
弾性波の音波や重力波の水面上の波などは,周波数(波長)の異なる波が干渉するとうなりを生じるが,光波などの電磁波では異なる波長の波の干渉は困難で,うなりのような現象は生じない。従って,光学における干渉は,同一の波長の光波が対象となる。
1881 年に開発されたマイケルソン干渉計(Michelson interferometer)は,フーリエ変換型赤外分光光度計などで広く利用されている。
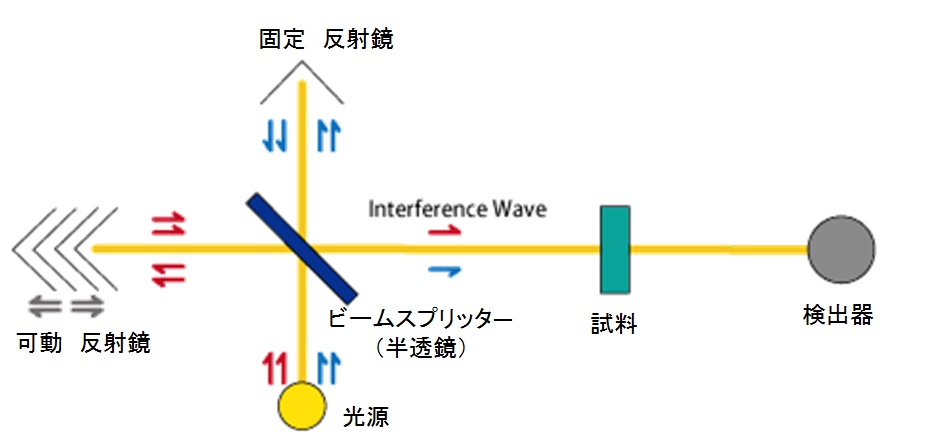
光束干渉計と FT–IR 基本装置構成(透過法)の模式図
マイケルソン干渉計は,最も一般的な干渉計で,ビームスプリッターを用いて光束(光のビーム)を 2 つに分割し,反射させた後,再び合流させることで干渉させる。
【波動の基礎】で紹介したように, 振幅 a で同じ方向に進む光線(光速 c :正弦波)の任意の点 x での変位 y は,
で与えられる。
ここで,係数 k ,波長 λ,周期 T ,振動数(周波数)ν,角振動数(角周波数)ωとの関係は,
である。
光源から出た光線は,マイケルソン干渉計のスプリッターで固定反射鏡と可動反射鏡の方向に分離される。なお,固定反射鏡と可動反射鏡での反射による位相の変化は,相殺されると仮定し,ここでは省略する。
反射した光線は,スプリッターで合流することになるが,合流直前の固定反射鏡で反射した光の変位( y1 )と可動反射鏡で反射した光の変位( y2 )は,それぞれの光線の経路の距離を x1 ,x2 とした時,
で与えられる。
ここで,kc = ωなので,kx1 = δ1 ,kx2 = δ2 とおくと,ビームスプリッターを経た 2 つの光線の変位 y は,重ね合わせの原理により,
ここで,
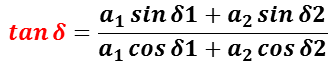
とできる。
光のエネルギーは,音波のエネルギーと同様に,変位の 2 乗に比例するので,光線の進行方向に垂直な単位面積を 1 周期 T の間に通過するエネルギー W は,
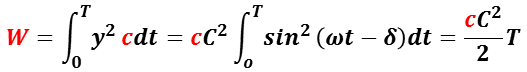
従って,単位時間当たりに通過するエネルギーは
I = W/ T = cC2/ 2
となり,光の強さ(平均のエネルギー)は,光の最大振幅( C )の 2 乗の 1/ 2 に比例する。従って,前出の式
から,δ1-δ2 が 2π,4πなどで光の強さが極大に,3 π,5 πでは極小になることが分かる。
ここで,光の波長λとした時,
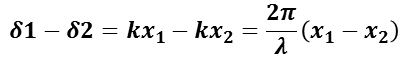
となるので,2 つの光線の光路差 (x1-x2)を変えることで,光の明暗の変化(干渉の結果)が得られる。
すなわち,光路差= m λで明るく(極大),光路差= ( m + 1/2 ) λで暗く(極小)になる。
【参考:基礎用語】
- 光路差(optical path difference)
1つの光波が2つに分れて別々の道を進み,その後再び合成されるとき,両波が分れてから合成されるまでのそれぞれの光学距離の差をいう。波長λの光波の光路差に 2π/ λを掛けると位相差になる。 - マイケルソン干渉計(Michelson interferometer)
アメリカの物理学者マイケルソンが考案した二光束干渉計で,分光分析機器などで用いられる。光速度の測定や光速度不変のの原理(特殊相対性理論)の導出につながるマイケルソンモーリーの実験に用いられた。 - マイケルソン(Albert Abraham Michelson)
アルバート・エイブラハム・マイケルソン(1852年 ~ 1931年)は,アメリカの物理学者,海軍士官で,マイケルソン干渉計の発明,光速度やエーテルに関する研究を行った。
ページの先頭へ
【反射で位相が変化する干渉の例】
マイケルソン干渉計や後述する回折格子の場合と異なり,干渉する光の一方の位相が変化する場合の干渉例を次に示す。
反射による位相の変化
【波動の基礎】で紹介したように,波の反射では,反射する界面が固定端か自由端かが反射波の位相に与える影響を紹介した。光波の反射においてもこの性質は成立し,固定端での反射波の位相がπずれ,自由端での反射波の位相はずれない。
光波の反射においては,固定端と自由端を厳密に区別することは困難であるが,概して,伝播する媒質と反射する媒質の屈折率の違いで分けられる。
すなわち,屈折率の小さい媒質から屈折率の大きい媒質へ入射する場合は,固定端での反射と同等に扱える。
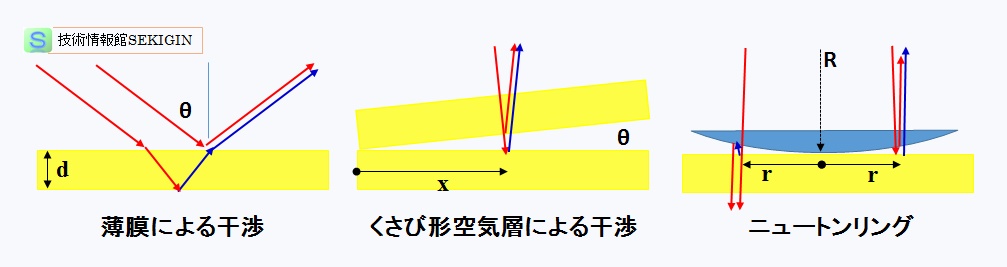
薄膜の干渉
下図の左に示すように,屈折率 n ,厚み d の薄膜に入射角θで入り,薄膜の底面で反射した光と薄膜の表面で反射する光の光路差は 2n d cos θとなる。
薄膜の屈折率が周辺より小さい場合は,薄膜表面は固定端での反射となり,底面の反射が自由端での反射となる。
一方,薄膜の屈折率が大きい場合は,表面が自由端での反射となり,底面が固定端での反射となる。
何れの場合も,薄膜の干渉では,光路差= m λで暗く(極小),光路差= ( m + 1/2 ) λで明るく(極大)なる。なお,m は整数である。
くさび型空気層による干渉
下図の中央に示すように,2 枚の板ガラスの片面接触で形成されるくさび型空気層による干渉である。
2 枚の板ガラスの成す角度θ,接線からの距離 x の空間の厚み d とすると,くさび型空気層の上面と下面から反射する光の光路差は,2d = 2x tanθとなる。なお,θが著しく小さいので tanθ≒θに近似できる。
一方,ガラスの屈折率は空気の屈折率より大きいので,ガラスを通過し空気層で反射した光は自由端での反射となり,空気を通過しガラス面で反射した光は固定端での反射(位相がπずれる)となる。
従って,光路差= m λで暗く(極小),光路差= ( m + 1/2 ) λで明るい(極大)平行な干渉縞が得られる。
ニュートンリング
下図の右に示すように,板ガラスの上に球面ガラスを乗せた時の干渉縞をニュートンリングやニュートン環という。
球面ガラスの曲率半径 R とした時,板ガラスとで形成される空気層の厚み d と中央の接触点かららの距離 r との関係は,R≫ d なので
![]()
と近似できる。
従って,光路差は,2d ≒ r2/ R とできる。
ニュートンリングでは,反射光を観察する場合と,透過光を観察する場合に分けられる。
反射光を観察する場合は,2 枚の板ガラスで形成したくさび型空気層による干渉と同じく,光路差= m λで暗く(極小),光路差= ( m + 1/2 ) λで明るい(極大)リング状の干渉縞が得られる。
透過光を観察する場合は,空気層でのガラス表面,すなわち固定端での反射が 2 回になるので,位相の変化が 2 π( 1 波長分)となるので,光路差= m λで明るく(極大),光路差= ( m + 1/2 ) λで暗い(極小)リング状の干渉縞が得られる。
干渉の例
ページの先頭へ
【回折とは】
JIS Z 8120 「光学用語 」では,回折(diffraction)を“a) 光が物体に当たったとき,直進せずに広がって進み,物体の影の部分にも光が回りこむ現象。b) 強度が断面内で一様でない光束において,光線が直進せずに広がって進む現象。”と定義している。
【波動の基礎】回折で紹介したように,波長の大きい音波やラジオ波などの長波長の電磁波では,障害物の影に回り込む現象を容易に体感できる。
可視光ほどの波長の短い電磁波では,体感できるほどの回析現象は観察し難い。しかし,周期的に並んだ格子(回折格子)を用いることで,回折した電磁波の干渉現象(干渉縞)を観察することができる。

回折格子の原理
nλ= d ( sinθm ± sinθ0 ) ( n は正負の整数)
すなわち,格子の溝の間隔 d ,波の入射角度θ0 を固定し,スリットを用いて角度θm を変えながら測定することで,回折光の波長λと強度を検出できる。
X線の結晶面での回折と干渉による干渉縞と結晶面間隔との関係式,すなわちブラック条件は,X線の波長分布を解析するX線分光法,結晶性物質の構造解析に用いられるX線回折法に用いられている。
ブラッグ条件とは,試料の結晶面と検出器の成す角度をθとすると,X線源と結晶面の成す角度は-θとなるので,干渉により強め合う限界は,d を結晶面の間隔,λをX線の波長,n を整数としたの次の関係式をいう。
2d sinθ = nλ
【参考:基礎用語】
- 回折格子(diffraction grating)
グレーティングともいい,平面鏡の鏡面に等間隔の多数の平行な溝を刻んだ平面回折格子,凹面鏡の鏡面に等間隔の多数の平行な溝を刻んだ凹面回折格子などがある。分光器の分散系としてプリズムの代りに用いられる。 - ブレーズド回折格子(blazed grating)
任意の回折次数で最大回折効率が得られるように最適化された特殊な反射型回折格子の一つで,エシェレット格子(echelett grating)とも呼ばれる。ている。 - ブラッグ散乱(Bragg scattering)
規則的に配列した原子によるX線や中性子の散乱をいう。 - ブラッグ(William Lawrence Bragg)
ウィリアム・ローレンス・ブラッグ(1890年 ~ 1971年)は,イギリスの物理学者で,現代結晶学の創始者のひとりといわれる。ブラックの条件で知られるX線による結晶構造解析の成果により,父のウィリアム・ヘンリー・ブラッグ(William Henry Bragg:1862年 ~ 1942年)と共にノーベル物理学賞を受賞している。
ページの先頭へ
【偏光とは】
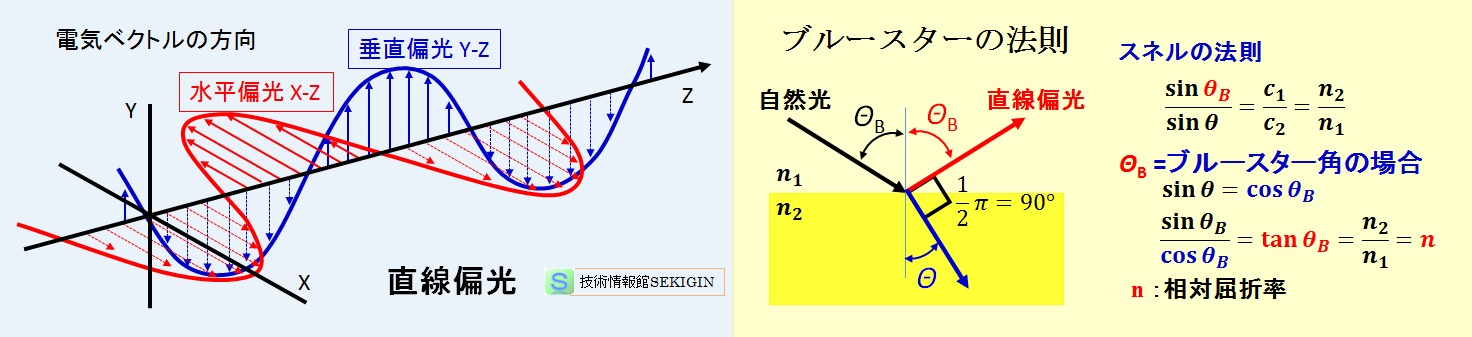
光波は電磁波の一種の横波であり,光の進む方向と電気ベクトルの方向とを含む面を偏光面といい,一般的な光波(自然光)の偏光面は,あらゆる方向に一様に分布しているが,方向分布が一様でない光を偏光という。
JIS Z 8120 「光学用語」では,偏光(polarized light)を“光波(電気ベクトル)の振動方向が規則的な光。 直線偏光,円偏光,だ円偏光がある。”と定義している。
なお,円偏光,楕円偏光など偏光面が光の進行につれて光の周波数で回転していくものを総じて回転偏光(rotatory polarization , rotatory polarisation)という。
直線偏光(linear polarization of light)
偏光面が一平面に限られている偏光で,平面偏光(plane polarized light)とも呼ばれる。
円偏光(circularly polarized light)
光波の電場成分または磁場成分の一方の振動に着目したとき,振動が光の伝播に伴って円を描く偏光で,回転方向により右円偏光と左円偏光がある
だ円偏光(elliptically polarized light)
電場(および磁場)の振動が時間に関して楕円を描く。直線偏光と円偏光の一次結合で表現される偏光で,最も一般的な偏光状態である。右楕円偏光と左楕円偏光がある。
偏光を得る原理
偏光していない自然光から直線偏光を取出す光学素子を偏光子(polarizer)という。光学素子を偏光の検出に用いるときは検光子という。
偏光を得る方法には,① 反射におけるブルースターの法則を利用するもの,② 結晶における複屈折の現象を利用するもの,③ 吸収性の結晶における二色性を利用するものなどがあげられる。
二色性(dichroism)は,多色性(pleochroism :たしきせい,たしょくせい)ともいわれ,JIS Z 8120 「光学用語」で“a) 異方性物質に光が入射する場合,その進行方向,振動面の方向によって波長選択吸収が存在する現象。b) 干渉フィルタにおいて,透過光と反射光との色が異なる現象。”と定義されている。
異方性は,光の吸収が光の波長とその振動方向によって異なるために生じる現象で,黒雲母などの鉱物に白色偏光を通じたとき,方向によって色が変る現象として広く知られ,偏光顕微鏡下でステージを回転させながら観察し,鉱物の同定などに用いられている。
【参考:基礎用語】
- 異方性(anisotropy)
JIS Z 8120 「光学用語」では“光学的性質が方向によって異なること。”と定義されている。 - 偏光角(angle of polarization)
JIS Z 8120 「光学用語」では,“屈折率 n の媒質から屈折率 n'の媒質に光が入射角θで入射するとθ= tan −1(n'/ n) の関係を満足する角θ。ブルースター角ともいう。”と定義している。
ページの先頭へ
【ブルースターの法則】
偏光を得る方法の一つに,反射におけるブルースターの法則を利用するものがある。
ブルースターの法則(Brewster's law)とは,光が相対屈折率 n の透明な媒質の表面に tanθ=n できまる特定の角度θで入射したとき,反射光は入射面(入射光の進行方向と入射点の法線を含む面)に垂直な振動面をもつ完全な直線偏光になるという法則である。
このθを偏光角(angle of polarization)またはブルースター角という。この時,スネルの法則に従う反射光と屈折光の成す角は直角( 1/ 2 π)になる。
例えば空気中でガラスに入射させる場合,θ≒57度とすれば反射する光により直線偏光が得られる。この現象を利用したものに,赤外線の偏光器,気体レーザー管の両端窓などがある。
偏光とは
ページの先頭へ
【複屈折現象】
偏光を得る方法の一つに,結晶における複屈折の現象を利用するものがある。
JIS Z 8120 「光学用語」では,複屈折(double refraction , birefringence)を“結晶その他の異方性物質に入射する光が,互いに垂直な振動方向をもつ二つの光波に分かれる現象。”と定義している。
また,異方性(anisotropy)は“光学的性質が方向によって異なること。”と定義されている。なお,光学的な異方性を示す物質を光学的異方体という。
方解石の結晶などの光学的異方体に光が入射したとき,一般的には,屈折光が 2 つの直線偏光に分かれ,2 つの偏光の偏光面は互いに垂直となる。
方解石などの単軸結晶,かんらん石などの二軸結晶(双軸結晶)は複屈折を示すことが知られている。
単軸結晶に光が入射すると,結晶内では光は複屈折を起して 2つに分れて進む。一方の屈折光は,通常の等方性媒質に対する屈折の法則に従って進む(光の速度が伝搬方向によらない)光で常光線と呼ばれる。
他方の屈折光は,光の速度が伝搬方向によって異なり,屈折角は入射角に対して複雑な変化をし,屈折光線の向きも必ずしも入射面にないなど屈折の法則が成立しない光で,異常光線と呼ばれる。
二軸結晶(双軸結晶)では,二つの屈折光とも異常光線である。
複屈折した光線について
常光線(ordinary ray)
JIS Z 8120 「光学用語」では,“光が複屈折性の結晶に入射して二つに分かれる場合,光の速度が伝搬方向によらない光線。”と定義している。
異常光線(extraordinary ray)
JIS Z 8120 「光学用語」では,“光が複屈折性の結晶に入射して二つに分かれる場合,光の速度が伝搬方向によって異なる光線。”と定義している。
複屈折する結晶について
単軸結晶(uniaxial crystal)
一軸結晶,一軸性結晶ともいわれ,1 つの光軸をもつ結晶をいい,結晶系の分類で六方晶系(石英,方解石),正方晶系(ジルコン),三方晶系(菱面体晶系ともいい,六方晶系に含められることがある)の結晶が該当する。
単軸結晶の光軸は,結晶の c 軸 (主軸)である。
同じ波長の同じ方向に進行する光でも,光の振動方向が主軸と垂直であるか垂直でないかによって屈折率が異なり,複屈折を示す。
二軸結晶(biaxial crystal)
双軸結晶ともいい,2 つの光軸をもつ結晶で,結晶系の分類で斜方晶系(かんらん石),単斜晶系(正長石,黒雲母,普通角閃石,普通輝石),三斜晶系(斜長石)の結晶が該当する。
結晶の光軸は,互いに直交せず,結晶軸と異なる方向を向く。
同じ波長の同じ進行方向の光の屈折率が光の振動方向によって異なり,複屈折を示す。
複屈折を利用した偏光子
偏光子には,方解石,水晶(石英)を用いた,ニコルプリズム,グラン・トムソンプリズム,ウォラストンプリズムなどがある。
ニコルプリズム(Nicol prism)
現在の使用実績は少ないが,歴史的に有名な光学素子で,直線偏光を得るために方解石で作ったプリズムである。
方解石の結晶を自然劈開面に沿って切り出し,画面が 68°になるように加工したものを対角線で切断(直角三角柱状)し,カナダバルサム(レンズの接着などに用いられるカナダバルサムノキから得られる樹脂)で再びはり合わせる。
入射光は複屈折により常光線と異常光線に分けられ,常光線は接合面で全反射し,異常光線だけが透過して直線偏光が得られる。
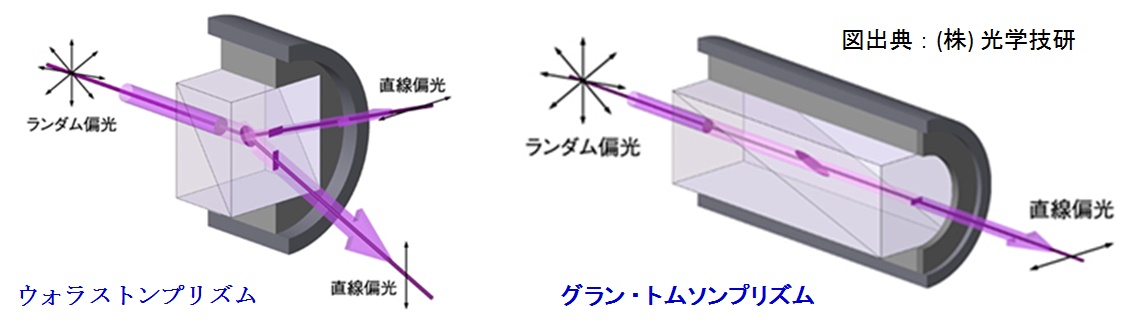
ウォラストンプリズム(Wollaston prism)
方解石や水晶を結晶軸が直交するように貼り合わせ,複屈折を利用した偏光子である。入射光をある開き角を成す直交する二つの偏光に分離でき,紫外線領域まで使用可能なため,各種分析器や偏光子として利用される。
グラン・トムソンプリズム(Glan-Thompson prism)
方解石のプリズムを 2 つ組み合わせ,空気層での全反射を利用し,異常光線だけを通過させる偏光子で,赤外線から紫外線まで利用可能なため現在広く使用されている。
偏光子の例
元図出典:(株) 光学技研
ページの先頭へ