物理 第六部:電磁気学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,電流と磁場の基本的な関連について, 【平行電流間の力】, 【電流の作る磁場】, 【コイルの作る磁場】, 【電流,磁場の方向】, 【ローレンツ力】, 【電磁誘導】 に項目を分けて紹介する。
【平行電流間の力】
平行な 2 本の導線(A ,B)に,直流電流 iA ,iB が流れているとき,導線間に力が作用することが知られている。
2 本の導線(A ,B)に作用する力の大きさは同じで,力の向きは,直流電流 iA ,iB の向きに応じ,同じ向きの時は引力,反対向きの時は斥力となる。
導線の間に働く力 F は,電流の大きさ,平行な区間の長さ( l )に比例し,導線の間隔( r )に反比例する。
ここで,比例係数を便宜的に 2km と置くと,導線に働く力 F は,
![]()
で表される。
ここで,km を上式が成立するように決めた単位は電流の電磁単位(CGS – emu)と呼ばれる。
すなわち,CGS電磁単位系で,1 CGS – emu の電流は
「真空中に 1 cmの間隔で同じ大きさの電流が流れているとき,両者の間に働く力が 1 cm につき 2 dyn (ダイン)であるときの電流」
と定義される。
電流の CGS 電磁単位系は, SI 単位系で 1 CGS – emu =10 A とできるので,長さl = 1 m ,間隔 r = 1 m ,電流の大きさ iA = iB = 1 A のとき,
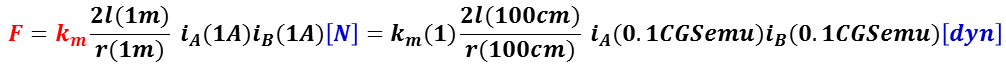
とできる。
すなわち,1 N = 105 dyn なので,SI 単位系での比例係数 km = 10–2 (dyn/ N) = 10–7 となる。
ここで,真空の透磁率は,μ0 = 4π×10–7 N A–2 で与えられるので,平行な電流に作用する力 F は, SI 単位系で示すと,
![]()
となる。
すなわち,電流の間に働く力には,電荷の間に働く力と同様の考え方が適用できる。
【参考:基礎用語】
- 電磁単位系(system of electromagnetic units)
磁極の強さを基本単位とする単位系で,磁気量を扱うのに便利である。頭文字をとって emu と略記する。
2つの磁荷の間に働く力を,CGS単位系の長さ(センチメートル; cm ),質量(グラム; g ),時間(秒; s )のほかに,クーロンの法則によって定義される単位系をCGS電磁単位系( CGS – emu )という。
CGS電磁単位系は,ウェーバーが提唱した電磁気の単位系である。 - ウェーバー(Wilhelm Eduard Weber)
ヴィルヘルム・エドゥアルト・ヴェーバー(1804年 ~ 1891年)は,ドイツの物理学者で,磁気の測定器具などの開発で電磁気学に大きく貢献し,磁束の SI 単位「ウェーバ」に名を残した。 - 透磁率(magnetic permeability)
透磁率は,導磁率ともいわれ,磁場の強さ H と磁束密度 B との間の関係を B = μH で表した時の比例定数μである。単位は H/ m (ヘンリー毎メートル),又は N/ A2(ニュートン毎平方アンペア)である。
ページの先頭へ
【電流の作る磁場】
前述のように,電流間に働く力は,電荷の間に働く力と同様の考え方が適用できる。すなわち,電流の周囲の空間が特殊な状態となり,この中に他の電流があると力を受けると考えることができる。
この特殊な空間が電流により作られる磁場(magnetic field)である。
ある時刻のある点に電場(electric field)の強さ E のベクトルが与えられたとき,この点では電場に対応したベクトル B が存在する。このベクトル B は磁束密度(magnetic flux density)といわれる。
【磁場とは】の繰り返しになるが,ある点における磁場の強さと方向を,1 Wb(ウェーバ)を 1 本とした磁力線の束で表したものを磁束(magnetic flux)や磁気誘導束といい,磁束の単位面積当たりの面密度が磁束密度で記号 B で表される。
平行な電流間に働く力は,導線の長さ,導線間の距離などの幾何学的条件により異なることを示した。
ここで,導線 B 上の微小部分 dSB を取り,流れる電流 iB としたとき,微小部分間に働く力 dF との関係が,
![]()
になることは明白である。
ここで,電荷の場合の点電荷に相当する i dS を便宜的(電流は電荷のように切り出せないので)に素片(element)として考えることができる。これを電流素片という。
これらから,微小部分間に働く力 dF は,導線 A の電流 iAの作る磁束密度 B の中に置かれた電流素片 i dS が受ける力(アンペールの力ともいわれる)と考えることができるので,
![]()
となり。すなわち,電流 iAの導線からの距離 r の位置の磁束密度の大きさは,
![]()
となる。
従って,磁場の強さ H と磁束密度 B の関係から,磁場の強さ H は,
![]()
で表される。
ページの先頭へ
【コイルの作る磁場】
ここで,電流 iAの導線を半径 r の円とした場合(円形コイル),円の中心の磁場の強さ H は,各電流素片の全周にわたる積分
H = iA/ (2r)
となる。
従って,導線を半径 r の円筒形に n 回巻いた円筒形コイル(ソレノイドともいう)の中心の磁場の強さ H は,円形コイルの n 倍となるので,
H = n iA/ (2r)
で表される。
ソレノイド(solenoid)とは,コイルの一種で,円筒形に絶縁された導体を螺旋状に長く巻いたもので,電流を流して磁場の発生を目的としたもの(電磁石),それを利用した装置(電磁弁,アクチュエータなど)を指す。
一般的に,コイルといった場合は,流れる電流によって形成される磁場にエネルギーを蓄えることができるインダクタ(inductor)やインダクション・コイルといわれる受動素子を指すことが多い。
インダクタは,一般的には導線を巻いた形状をしている。複数回巻くことでアンペールの法則に従いコイル内の磁場が強くなる。コイル内の磁場の変化に比例してファラデーの電磁誘導の法則に従い誘導起電力(自己誘導;self-induction)が生じる。また,誘導電流は,レンツの法則に従い磁場の変化を妨げる方向に流れる。
このように,インダクタは交流電流を遅延させ再形成する能力があり,コンデンサなどを組み合わせることで,特定の周波数の信号だけを取り出す共振回路やフィルタ回路を構成できる。
【参考:基礎用語】
- アンペールの法則(Ampère's circuital law)
フランスの物理学者アンペールが発見した電流のまわりにできる磁場の関係をあらわす法則である。電流のSI単位アンペア(A)は,アンペールの業績にちなんで用いられている。 - アンペール(André-Marie Ampère)
アンドレ=マリ・アンペール(1775年 ~ 1836年)は,フランスの物理学者,数学者で,アンペールの法則の発見など電磁気学の創始者の一人とされる。なお,電流のSI基本単位「A:アンペア」はアンペールの名に因んで命名されている。 - ファラデー(Michael Faraday)
マイケル・ファラデー(1791年~1867年)は,イギリスの化学者,物理学者で,ファラデーの電磁誘導の法則,ファラデーの電気分解の法則,ファラデー定数など電磁気学,電気化学への貢献で知られる。 - 自己誘導(self-induction)
閉回路の電流が時間的に変化すると,電流の変化を妨げる向きに回路に逆起電力が生じる現象をいう。 - レンツの法則 (Lenz's law)
ロシアの物理学者ハインリヒ・レンツが発見した電磁誘導に関する法則で,“誘導電流の方向は誘導電流の原因を妨げる方向と一致”するという法則である。例えば,コイルの軸方向に棒磁石を近づけると,誘導電流は,棒磁石の接近を妨げる向きの磁場が発生する方向に流れる。 - レンツ(Heinrich Friedrich Emil Lenz)
ハインリヒ・レンツ(1804年 ~ 1865年)は,ロシア帝国の物理学者で,レンツの法則で知られる。
ページの先頭へ
【電流,磁場の方向】
電流の向き,磁場の向き,及び力の方向に関しては,フランスの物理学者アンペールの発見した右手の法則(右ねじの法則),やイギリスの物理学者フレミングが考案したフレミングの右手の法則,フレミングの左手の法則が理解し易い。
右手の法則(right-hand rule)
電流の周りの磁場の向きを示すアンペールが発見した法則である。
右手を握って親指を立てたとき,親指の方向を電流の向きとすると親指以外の指の方向が磁場の向きに一致する。
日本では「右ねじの法則」ともいい,電流を右ねじが進む方向に直進させると磁場が右ねじの回転方向に一致する。
フレミングの右手の法則(Fleming's right hand rule)
外部磁場内を運動する導体内に発生する起電力(電磁誘導)の向きを覚えやすくするためにフレミングが考案した方法である。
右手の中指と人差し指と親指をたてて互いに直角の関係にしたとき,人差し指が磁力線の方向,親指が導体の動いた方向,中指が導体に発生する起電力による電流の方向を向く。
フレミングの左手の法則(Fleming's left hand rule)
外部磁場内において,電流が流れる導体に発生する力(ローレンツ力)の向きの関係を示すフレミングが考案した方法である。
左手の中指と人差し指と親指を立てて互いに直角の関係にしたとき,中指が電流(電荷の速度)の磁場に対する垂直成分の方向,人差し指が磁場の方向,親指が導体に発生する力の方向を向く。
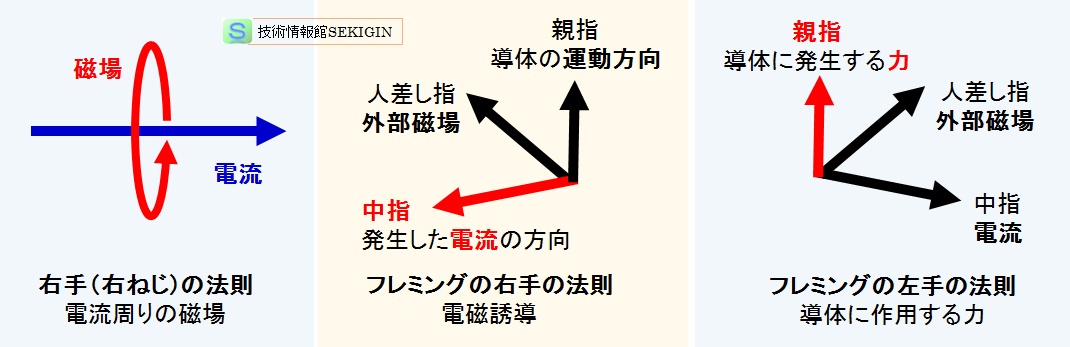
磁場,電流,力の関係
【参考:基礎用語】
- フレミング(Sir John Ambrose Fleming)
ジョン・アンブローズ・フレミング(1849年 ~ 1945年)は,イギリスの物理学者,電気技術者で,真空管の発明,フレミングの法則の考案で知られる。 - ローレンツ(Hendrik Antoon Lorentz)
ヘンドリック・アントーン・ローレンツ(1853年~1928年)は,オランダの物理学者で,ローレンツ力,ローレンツ変換などで知られる。 - クーロン(Charles-Augustin de Coulomb)
シャルル=オーギュスタン・ド・クーロン(1736年 ~ 1806年)は,フランスの物理学者で,帯電した物体間に働く力を測定からクーロンの法則を発見した。業績に因んで,電荷の単位に「クーロン; C 」が用いられている。 - 電気量の単位
電気量(quantity of electricity)の単位のクーロン( C )は,SI 単位系では,1 アンペア( A )の定常電流が 1 秒間( S )流れたときに運ばれる電気量(電荷の量)に対する組立単位( 1C = 1A・S )である。
ページの先頭へ
【ローレンツ力】
平行な電流の間に力が働くことは既に紹介した。この現象は,一方の電流が作る磁場の中を運動する荷電粒子の受ける力と理解できる。
荷電粒子が磁場の中を運動するときに,荷電粒子が受ける力は,オランダの物理学者ローレンツに因んでローレンツ力(Lorentz force)と呼ばれる。
ローレンツ力は,電動機(モータ),質量分析などの動作原理に用いられる身近な力である。
荷電粒子 1 個の電荷を q クーロンとし,単位長さ( 1 m )に荷電粒子が n 個の密度で存在していると仮定する。すなわち,単位長さ当たりで qn クーロンの電荷が存在していると考えられる。
この荷電粒子が一定方向に速度 v(秒速)で移動している場合に,ある断面を単位時間( 1 秒)に通過する電荷の量を電流 i とできるので,電流と電荷の移動量とは i = qnv の関係になる。
ここで,前述の【電流の作る磁場】で紹介したアンペールの力の式における電流 iB に電荷の移動量を代入できる。なお,代入したアンペールの力の式において電荷粒子の密度 n と微小部分 dS の積は,電荷の個数になるので,これを N と書き表すと,
![]()
が得られる。
アンペールの力では,電流の微小部分にかかる力の大きさを示したが,この式では,微小部分に含まれる荷電粒子に作用する力の大きさを示す。
そこで,両辺を荷電粒子の数 N で割ると,荷電粒子 1 個の受ける力を表すことになる。また,電荷の移動方向は電流の方向と一致するので,電荷q の荷電粒子 1 個が磁束密度 B の磁場中を速度 v で運動するときに受ける力 F は,
![]()
と磁束密度とのベクトルの外積で書ける。
従って,磁場の方向と荷電粒子の運動の方向が角度 θを成す時は,荷電粒子が受ける力は,磁場との垂直な速度成分 v sinθを用いて求められる。
ページの先頭へ
【電磁誘導】
電磁誘導(electromagnetic induction)
磁場の変化によって導体や電気回路に起電力(誘導起電力;induced electromotive force)を生じる現象で,イギリスの物理学者ファラデーとアメリカの物理学者ヘンリーがほぼ同時期に発見したといわれる。
この場合に,閉じた電気回路では電流が流れ,これを誘導電流(induced current)という。誘導起電力,誘導電流の向きは,磁場の変化を打消すように起る(レンツの法則)。
ある閉回路を貫く磁束を Φ ( Wb :ウェーバ)としたとき,この回路に生じる誘導起電力 E( V :ボルト)は,磁束の変化の速度に比例( E = ‐𝜕φ/ 𝜕 t )する。この関係をファラデーの電磁誘導の法則(Faraday's law of induction)という。
実用で用いられる N 巻きコイルの場合は,各 1 巻きを貫く磁束の時間変化が等しいと官下られる場合は,誘導起電力は 1 巻きコイルの N 倍になる。
電磁誘導は,発電機,交流モーター,変圧器など多くの電気機器の動作原理として広く知られる。他には,コイルに強い電流を流すことで発生する強力な磁場の上に導電性の鉄やステンレスなどの金属を置くことで,電磁誘導で発生した渦電流により加熱する電磁誘導加熱(induction heating :略語 IH ),ローレンツ力や誘導磁場により推進するレールガン,リニアモーター等にも応用されている。
相互誘導(mutual induction)
二つのコイル( A , B )が磁気的に結合しているとき,2つのコイルに流れる電流が互いに影響を及ぼす現象をいう。例えば,回路 A を流れる電流が変化(時間 Δt の間に ΔI 変化)したとき,電磁誘導により,回路 B に誘導起電力(-M(ΔI/Δt) )が生じる現象である。この時,比例定数 M を相互インダクタンス(mutual inductance)という。
インダクタンス(inductance)とは,コイルを流れる電流を変化させたとき電磁誘導によりそのコイル,あるいは他のコイルに発生する起電力の大きさを表わす量をいい,単位には,アメリカの物理学者ヘンリーに因んでヘンリー( H )が用いられる。
【参考:基礎用語】
- ファラデーの電磁誘導の法則(Faraday's law of induction)
電磁誘導で,1 つの回路に生じる誘導起電力の大きさは,回路を貫く磁界の変化の割合に比例する。すなわち,ある閉回路を貫く磁束を Φ ( Wb :ウェーバ)としたとき,この回路に生じる誘導起電力 E( V :ボルト)は,磁束の変化の速度に比例( E = ‐𝜕φ/ 𝜕 t )する。 - ヘンリー(Joseph Henry)
ジョセフ・ヘンリー(1797年 ~ 1878年)は,アメリカの物理学者で,イギリスの物理学者マイケル・ファラデーと同時期に電磁誘導の発見,自己誘導現象の発見などで知られ,インダクタンスの SI 単位ヘンリーに名を残した。
ページの先頭へ