物理 第四部:波・波動の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,最も身近な音の発生に関し, 【発音体の振動】, 【弦の振動】, 【弦を伝わる波】, 【気柱の振動】, 【音波の速度】, 【気柱の振動数】 に項目を分けて紹介する。
【発音体の振動】
ここでは,発音体として弦,気柱の振動について紹介する。
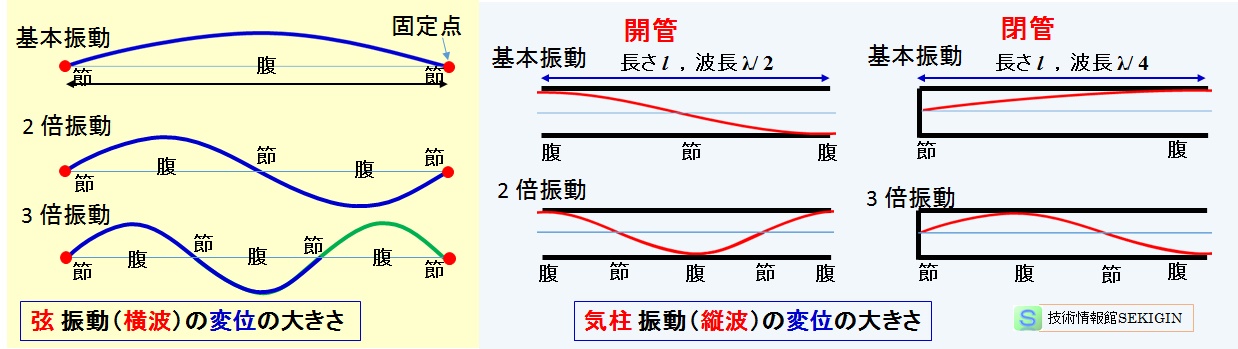
弦の振動,気柱の振動(模式図)
- 発音体(sounding body , sound producing body)
弦やリードなどの自体が振動し,音源となるものをいう。 - 弦(string)
弦は,発音体として弦楽器に用いられる(動・植物・金属製)糸,弓のつる,半月(下弦・初弦・上弦の月),直角三角形の斜辺(正弦・余弦)などの意味で用いられる。 - 気柱(air column)
管の中の柱状の空気をいう。気柱の共鳴により音が大きくなる効果があり,管楽器の発音体として用いられる。 - 波動(wave motion)
空間のある点で生じた変化(振動など)が隣接する部分に次々と有限の速さで伝わる現象で,波ともいわれる。波動の性質は,周期,振幅,波長などで表され,反射,屈折,干渉,回折などの現象を示す。
一般的に,波動を扱う分野では,物理現象として音や光などの振動(周期的な現象)が扱われる場合が多い。しかし,周期性は波動に必須の性質ではない。このため,波動では,振動が連続的に発生し伝搬する連続波(continuous wave),単独もしくは短い振動が伝搬するパルス波(pulse wave)に分類して扱われることが多い。
波動は,媒質の振動が波の進行方向に対して平行な縦波(longitudinal wave)と波の進行方向に対して垂直な横波(transverse wave)に分けられる。
ページの先頭へ
【弦の振動】
ピアノ,バイオリンやギターなどの弦楽器の音は,弦(string)の振動(横波)が空気を振動させることで発生した疎密波(弾性波,縦波)である。この場合,弦は発音体といわれる。
長さ l の弦を適当な張力 S で両端を固定し,弦をはじいて振動させた時,弦に沿って波が伝わる。
後述するように,弦の長さと張力により定まる波は,固定端で反射し,他端の方向に向う。これの繰り返しで,弦は振動し続ける。
このとき,弦の両端が固定されているので,両端で変位のない波,すなわち両端が節となる波のみが残り,それ以外の波は消える。なお,最も変位の大きい部位を振動の腹という。
従って,振動し続ける波の波長λと弦の長さ l との間には次の関係が得られる。
l = n λ/ 2 ∴ λ= 2 l / n
ここで,n は整数で,弦の振動で現れる腹の数である。現れる波のうち,n = 1 の振動を基本振動,n = 2 の振動を 2 倍振動, n = 3 の振動を 3 倍振動・・・という。
【参考:基礎用語】
- 弾性波(elastic wave)
音波や地震波などの弾性体内を伝わる波をいう。
弾性体が固体の場合は,変位方向により,体積変化に伴う体積弾性による縦波,体積変化がなく形状変化に伴う形状弾性による横波に分けられる。
弾性体が流体の場合は,密度変化(体積変化)に伴う縦波だけで,横波はない。 - 疎密波(compression wave)
圧縮波ともいい,縦波の 1 種で,音波や地震の P 波など流体や弾性体に加わった圧力で局所的な密度変化が生じた波である。 - 固有振動(proper vibration)
両端を固定した弦,管の中の空気(気柱)などを振動させたときに,特定の振動数の振動のみが発生することを固有振動といい,その振動数を固有振動数や固有周波数という。 - 基本振動(fundamental vibration)
基音(fundamental tone),基本波ともいい,固有振動数が倍数関係にある固有振動のなかで,最小の振動数(単振動)をいう。 - 倍音(overtone , harmonic sound , harmonics)
倍振動ともいい,基本振動の整数倍の振動数をもつ固有振動をいう。弦の振動は基本振動と多数の倍音との合成として表すこと(調和解析:harmonic analysis)ができる。 - 調和解析(harmonic analysis)
関数や信号を基本波の重ね合わせとして表現する数学の一分野で,フーリエ級数,フーリエ変換などの一般化に関する研究分野。
ページの先頭へ
【弦を伝わる波】
波の速度
張力 S ( N = kg m S-2 ) で張られた,密度ρ ( kg m-3 ) の弦が振動しているときの波の速度を求める。
振動の変位が小さい場合に,弦の長さの変化(伸び)が無視できるとした場合に,張力 S に変化が無く一定とできる。
弦の中で,dx 離れた 2 点が波のないときの位置から変位した時を考える。張力は弦の接線の方向に作用するので,2 点の変位前後の接線の成す角度をθとθ’ としたとき,2 点間の部分(質量 ρdx )の運動方程式( ma = F )は,
![]()
となる。θが小さいので,
![]()
と考えられる。ここで,
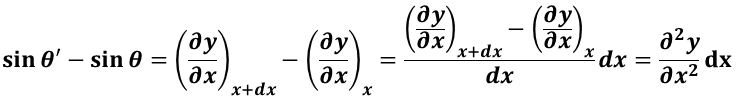
なので,運動方程式は,
![]()
となる。
これは,波動方程式
![]()
となるので,弦を伝わる波の速さ c は,
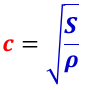
すなわち,弦を伝わる波の速さは,弦の張力 S と弦を構成する材料の密度ρで与えられる。
弦の振動数(固有振動数)
波の速さ c は,波の波長λと振動数 f の積で得られるので,振動数( f )は,
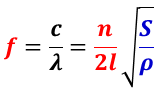
で与えられる。
弦の周波数(固有振動数)は,弦の長さ,弦の密度,張力で定まる。
【参考:基礎用語】
- 張力(tension)
垂直応力が引き合う場合,すなわち,物体のある平面に垂直方向に作用する引っ張り合う単位面積当たりの力をいうが,一般的には,単に引っ張る力の意味で用いることも少なくないので,単位を記すなど文脈において,単位面積当たりの力(応力)なのか外力としての引く力かを明確にしておくと誤解を避けられる。 - 運動の法則(law of motion)
第1法則(慣性の法則:law of inertia):外から力が作用しない限り,質点は静止又は等速直線運動する。
第2法則(ニュートンの運動方程式:Newton's equation of motion):質点の加速度 a は,そのとき質点に作用する力 F に比例し,比例係数 m(質点の質量)に反比例 ma=Fする。
第3法則(作用・反作用の法則:law of action and reaction):二つの質点 A , B の質点 A から質点 B に力(作用)を及ぼすと,同時に質点 B から質点 A に力(反作用)が及ぼされ,作用と反作用は大きさが等しく逆向きである。 - 波動方程式(wave equation)
波動に関する運動方程式で,空間座標と時間とを独立変数とする波を記述する偏微分方程式をいう。 - 偏微分(partial differential)
二つ以上の変数を持つ関数 f において,一つの変数にだけ注目し,他の変数は固定して定数とみなし,注目した変数の関数として微分することをいう。例えば,関数 f を x で偏微分するという場合は,関数 f の偏微分 𝜕 f/ 𝜕x と表す。
ページの先頭へ
【気柱の振動】
フルート,トランペットなどの管楽器やパイプオルガンなどは,管の中の空気(気柱)の振動で音を伝えている。
ここで扱う管は,両端が解放された管(開管)と,一端が閉じた管(閉管)に分けられる。
波動の基礎で紹介したように,液体や気体の中では,ずれに対する弾性が無く,圧縮に対する弾性のみであるため,横波は現れず縦波(疎密波)のみが起きる。
閉管の閉じた端では,空気分子が移動(変位)できないので,弦の振動の場合の節となる。従って,両端が閉じた管では,両端が固定された弦と同様に考えられる。
一方,開いた端(管口)の外は,管壁に閉じ込められた大気と異なり,自由に動ける大気が広がっている。このことは,管の内外は同じ空気分子で構成されているが,あたかも異なる媒質が管口付近で接触しているように作用する。すなわち,この境界面で音の反射が起きる。
管内の空気は激しく振動し,圧力変動も著しいが,管口の少し外側では,一定の外気圧に保たれるので,管口付近で最も変位の大きい振動の腹になる。
空気の振動の腹は,細い管の場合は管口の半径の概ね 0.6 倍の距離だけ外側に離れた位置にある。これを開口端補正という。
従って,両端が開いた開管では,両端が腹となる振動で,波の波長λと管の長さ l との間には,両端が節となる弦と同様の関係が得られる。
l = n λ/ 2 ∴ λ= 2l/ n
ここで,n は整数で,振動で現れる節の数である。現れる波のうち,n = 1 の振動を基本振動,n = 2 の振動を 2 倍振動, n = 3 の振動を 3 倍振動・・・という。
一方,片端が閉じた閉管では,閉じた端部が節,開いた端部(管口)が腹となる振動である。このため,開管の波に比較して 1/ 4 波長短い波となる。
すなわち,波の波長λと管の長さ l との間には,
l = (2n-1)λ/ 4 ∴ λ= 4l/ (2n-1)
の関係が得られる。ここで,n は整数で,n = 1 (2n-1=1)の振動を>基本振動,n = 2 (2n-1=3)の振動を 3倍振動, n = 3 (2n-1=5)の振動を 5 倍振動・・・という。
ページの先頭へ
【音波の速度】
音波は疎密波で,気体中での急激な疎密振動は断熱的に起ると考え,1816年にラプラスがポアソンの法則(Poisson's law: PVγ = 一定)を用いて,圧力 P ,密度 ρの気体中の音速を導いた。
気体の定圧比熱容量と定積比熱容量の比である比熱比 γ,気体定数 R ,気体温度 T ,気体の平均分子量 M とした時の乾燥気体中の音速 c は,
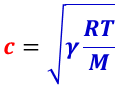
で与えられる。
また,気体の状態方程式(PV=nRT),気体の密度(ρ=m/V),平均分子量(M=m/n)から RT/ M=P/ ρ が得られので,
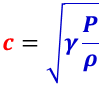
でも与えられる。
なお,比熱比γは,分子の構造によって決まる。理想気体の場合,He などの単原子分子はγ=5/3( He 1.66 ),O2 ,N2 などの二原子分子はγ=7/5( O2 1.40 )となる。
【参考:基礎用語】
- ポアソンの法則(Poisson's law)
理想気体が準静的な断熱変化を行う場合の圧力 P と体積 V の関係をいう。
pVγ = 一定
ここで,指数のγは比熱比で与えられる。 - 比熱容量(specific heat capacity)
単に比熱とも呼ばれ,単位は J・kg‐1・K‐1 である。なお,一般的には,温度によって変化するので,比熱容量を表示する場合は,温度の指定が必要である。
原子量,分子量(モル)当たりの熱容量を原子熱(比熱容量×原子量),分子熱(比熱容量×分子量)という。分子熱は,モル比熱,モル熱容量とも呼ばれる。
液体や固体の体積は,温度による極端な変化はないが,気体は,温度によるエンタルピーや体積の変化が大きいため,圧力を一定に保ちながら測定した値と体積を一定に保ちながら測定した値で大きな違いがでる。
前者を定圧比熱容量(specific heat capacity at constant pressure),後者を定積比熱容量(specific heat capacity at constant volume)や定容比熱容量といわれている。 - 比熱比(specific heat ratio , heat capacity ratio)
1 モル当たりの定圧比熱容量( Cp )と定積比熱容量( CV )との比( Cp/ CV )をいい,通常は記号γ(又はκ)を用いて表す。 - 理想気体(ideal gas)
理想気体は,完全気体( perfect gas )ともいい,現実には存在しない理想的な気体である。すなわち,ボイル=シャルルの法則を状態方程式とし,内部エネルギーは体積によらず温度だけの関数となり,断熱変化に対してポアソンの法則に従う。
このためには,気体を構成する粒子(分子や原子など)の体積と,粒子間の相互作用をともに無視できる系として扱われる。 - 気体の状態方程式(equation of state)
ボイルの法則とシャルルの法則を合わせた法則で,“気体の圧力 P は体積 V に反比例し,熱力学(的)温度 T に比例”。気体の状態方程式( PV / T = 一定)として知られる。
ページの先頭へ
【気柱の振動数】
波の速さ c は,波の波長λと振動数 f の積で得られるので,振動数( f )は,f = c/ λで与えられるので,
開管の周波数は,
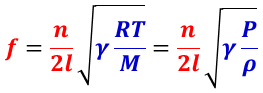
で与えられ,閉管の周波数は,
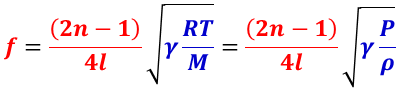
で与えられる。すなわち,気体の状態(気圧,温度,密度など)が一定であれば,周波数は管の長さで定まる固有振動数となる。
なお,厳密には,前出したように,管の長さに対しては,開口端の補正が必要である。
ページの先頭へ