物理 第四部:波・波動の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,双眼鏡やカメラで身近な光学として, 【幾何光学とは】, 【平面波と球面波】, 【レンズの原理】, 【屈折率の関係式】, 【結像公式】, 【薄レンズの公式】, 【レンズによる結像】, 【幾何光学関連の基礎用語】 に項目を分けて紹介する。
【幾何光学とは】
幾何光学(geometrical optics)は,光伝播を光線という概念で捕え,直進性,反射,屈折など光線の経路を幾何学的に論じる分野である。
すなわち,干渉や回折などの波動的現象を考えず,光線は一様で,媒質内では直線をなして進むと考えて,レンズで構成される光学系などの実用的な特性の解明を主目的としている。
【波動の基本性質】で紹介したように,空間を伝わる波の位相の等しい点を連ねた面を波面(wave front)といい,波面が球面状の波動を球面波(spherical wave),平面状ならば平面波(plane wave)という。
波動の伝わる方向は,波面に垂直な方向である。この波動の進む線を射線という。一本一本の射線,又はそれらの集合を光線(ray of light)と呼ぶ。
光線は,均質な媒質の中では直進し,異なった媒質の境界面で,光線の反射,屈折が起きる。なお,反射と屈折は,入射面内の法線に対して,入射側と反対側で起きる。
反射(reflection)
【波動の基本性質】で紹介したように,波動が 1 つの媒質から他の媒質へ向って伝搬するとき,媒体の境界面(界面)で一部分又は全部が元の媒質内へ戻る現象をいう。
全部戻る場合を全反射という。なお,波の反射では,入射面内で法線に対して,入射した側と反対側に反射し,入射角(angle of incidence)と反射角(angle of reflection)は相等しい。
屈折(refraction)
波動が進む 1 つの媒質から他の媒質の中に入り込む場合に,その界面で進行方向が変化する現象をいう。
物質(媒体)を構成する分子・イオンの空間分布が方向に依存しないものを等方性媒質間といい,2 種の等方性媒質で起きる屈折では,入射角 i と屈折角 r との間にスネルの法則が成り立つ。
屈折の法則ともいわれるスネルの法則は,媒質中の波動について,下記の位相速度(νi ,νr ),入射角( i ),屈折角( r )の関係を表した法則である。この法則は,ホイヘンスの原理によって説明される。
sin i / sin r =νi / ν r = 一定(相対屈折率)
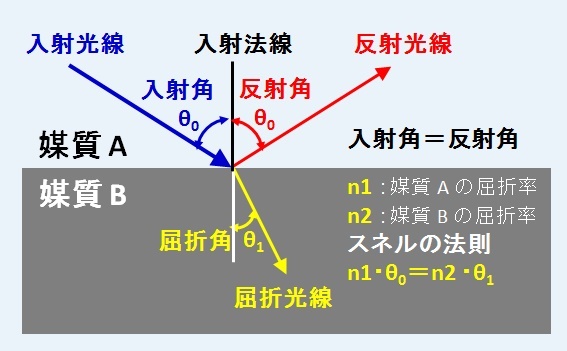
光線の基本特性(模式図)
ページの先頭へ
【平面波と球面波】
光線は,光源との距離が近い場合などの光源(一点)から四方八方に発散し波面が球面状の球面波,太陽と地球の関係のように光源が非常に遠い場合やレーザー光などの波面が平面状の平面波(平行光線)に分けられる。
なお,球面波には,光線の 1 点から発散する場合の他に,光学系で平面波から作られた球面波のように 1 点に収束する場合がある。
下図に示すように,媒質 A 中に,媒質 B があり,その界面が球面となっている場合を考える。
界面の曲率中心に点光源(point source)がある場合は,光線は界面に対し垂直に当たるので,入射角がゼロとなるので,媒質間の屈折率が異なっていても光線は屈折せず進む。
点光源が曲率中心からずれた位置にある場合には,界面を通過した光線は屈折する。
ここで,下図にあるように,媒質 A から界面に対し入射光線が当たる場合に,入射光線の延長線と球面の軸( x )との交点を物点(object point)といい,媒質 B との界面で屈折した実際の光線と球面の軸との交点を球面に対する物点の像点(image point)という。
このように,1 点から出発した球面波を別の点に中心のある球面波に変換する作用を持つものはレンズ作用があるという。
一般に,光源に相似の像を作ることができるものを結像系という。顕微鏡やカメラのレンズなどは,優れた結像系を作るため,複数の球面の曲率中心が一直線上にあるように軸を共通にして組み合わせている。これを共軸球面系といい,軸をその光学系の主軸や光軸(optical axis)という。
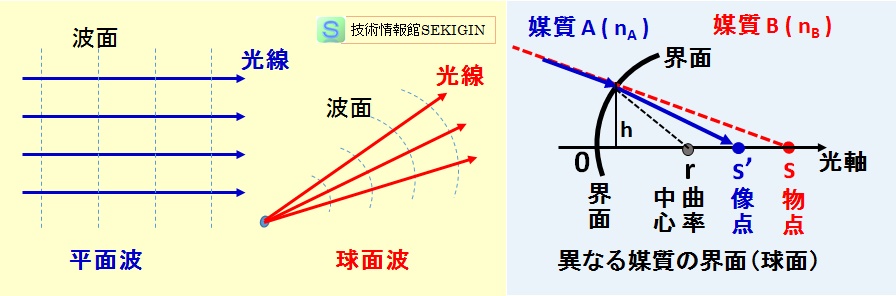
平面波,球面波,結像((模式図)
ページの先頭へ
【レンズの原理】
前出のレンズ作用を示す場合,すなわち物点(点光源)から出た光線が,屈折率の異なる媒質が球面で接触している場合について考える。
レンズを考察する際に活用される基本方程式を次に示す。
屈折率の関係式
n・ sin θ = 一定
結像の公式
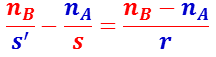
(薄)レンズの公式
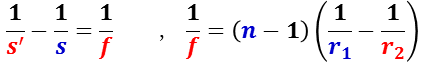
ページの先頭へ
【屈折率の関係式】
スネルの法則は,屈折の法則ともいわれ,媒質中の波動の位相速度(νi ,νr ),入射角( i ),屈折角( r )の関係を表した法則で,ホイヘンスの原理によって説明できる。
sin i / sin r =νi / νr = 一定(相対屈折率)
屈折率(refractive index)とは,JIS Z 8120 「光学用語 」では“真空中の光の位相速度と媒質中の光の位相速度との比。量記号 n で表す。”と定義される。
ここで,真空中の光の位相速度を C ,入射側の屈折率を n1 ,屈折側の屈折率を n2 とすると,
C/ νi =n1 ,C/ νr = n2
となるので,スネルの法則は,
sin i / sin r =νi / νr = n2/ n1
又は,
n1 sin i = n2 sin r
が得られる。
すなわち,境界面がすべて平行な複数の媒質を透過する光線は,
n・ sin θ = 一定
の関係が成立し,これを屈折率の関係式という。
ページの先頭へ
【結像の公式】
下図の左において,A を原点にとり,光軸方向に,C ,O’ ,O の座標を r ,S’ ,S とする。
図の場合は,媒質 B (屈折率 nB )の中にC ,O’ ,O があるので, r ,S’ ,S は正となる。
なお,一般的に物点(点光源)O が媒質 A にある場合が多く,この場合は s は負となるが,この光線が媒質 B の一点に収束する場合は,その点が O となるので,s を正とし,この場合の物点を虚光源ということがある。
ここで,AC とBC の成す角φの点 B と点 O を通る線の延長上の媒質 A から入射した光線が,屈折して O’に達した時,屈折率の関係式より
nA sin i = nB sin i’
h = r sin φ
となる。
ところで,OC = s – r ,O’C = s’ – r ,CB = r なので,△CBO と△CBO’ には,
( s – r )/ sin i = r/ sin u ,( s’ – r )/ sin i' = r/ sin u’
の関係がある。ここで,BO = p ,BO’ = P’ と置けば,
p sin u = p’ sin u’ = h
なので,以上から
![]()
が得られる。これを整理すると,
![]()
となる。
ここで,p2 = s2 – h2 , p’2 = s’2 – h2 なので,s と s’ の絶対値が h より著しく大きい場合には,次の近似式が適用できる。
![]()
さらに,h2/ s2 以上の項を省略できるので,上式から,
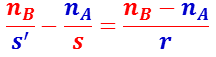
が得られる。これを結像公式という。
反射鏡の場合は,nB = –nA ,i' = i と置くことで,形式的にそのまま用いることができる。
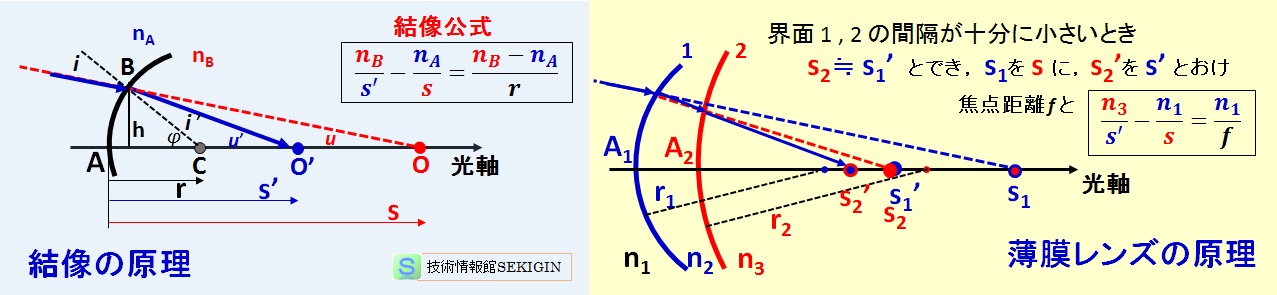
薄膜レンズの原理(模式図)
ページの先頭へ
【薄レンズの公式】
ここでは,カメラなどで用いられる共軸球面系,すなわち複数の球面の曲率中心が一直線上にあるように軸(主軸や光軸という)を共通にしたレンズを考える。
上図の右に示すように,屈折率 n1 ,n2 ,n3 の媒体,が曲率半径 r1 ,r2 の 2 つの球面を界面として配置された場合を考える。なお,ここでは屈折率 n1 = n3 の場合も含まれる。
球面 1 の結像の公式と球面 2 の結像の公式は,
![]()
![]()
である。
物点( s )と像点( s’)は,光軸と球面のそれぞれの交点から距離であるが,交点 A1 とA2 の距離が物点や像点の距離に比較して著しく小さい場合には,2 つの主点が一致すると近似(薄レンズ近似)できるので,s2 = s1’とできる。
従って,球面 1 と球面 2 の結像の公式の和は,
![]()
となる。
焦点(focal point)について
物点の距離 s1 = ∞の時の像点の位置を像空間焦点という。すなわち,光軸に並行な光線束がレンズを通過して光軸上の 1 点に集まる点である。
像点の距離 s2’= ∞ の時の物点(点光源)の位置を物空間焦点という。すなわち,この点を出た光線束は,レンズ通過後に,光軸に並行に進む。
物空間焦点からレンズまでの距離の物焦点距離 f は,次式で与えられる。
![]()
ここで,物点 s1 = s,像点 s2’= s’とおくと
![]()
が得られる。
ここで,大気中にレンズを置いた場合など,屈折率 n1 = n3 = 1 ,レンズの屈折率 n2 = n とした時の式を薄レンズの(結像)公式という。
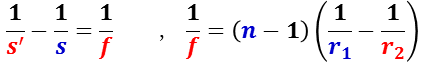
この式は,上図に示すように,光の進行方向を正にとっているので,レンズの左側(距離 a )に物点(光源),レンズの右側(距離 b )に像点がある場合は,s = - a ,s’ = b となりレンズの公式は
1/ b +1/ a = 1/ f
となる。
レンズに厚み d がある場合の焦点距離は次式で近似される。
![]()
ページの先頭へ
【レンズによる結像】
レンズの構造について
レンズによる結像を考えるうえで,焦点,物点,像点の距離を定義する際の基準が必要である。この基準となる面を主面,光軸と主面の交点を主点という。
主面とは,光軸に平行な光線を入射したとき,入射前および出射後の光線を延長した 2 直線の交点が描く軌跡をいう。
薄レンズ 1 枚の場合は,レンズの中心を主面や主点に近似できるが,レンズが厚くなると,下図に示すように,平行光線の方向により主面と主点が 2 つ存在する。薄レンズを複数組み合わせた場合も同様になる。
なお,図中の前側主点は物空間主点,後側主点は像空間主点ともいわれる。また,レンズを組み合わせた場合の焦点 F は組み合わせレンズの物空間焦点,焦点F’は組み合わせレンズの像空間焦点という。
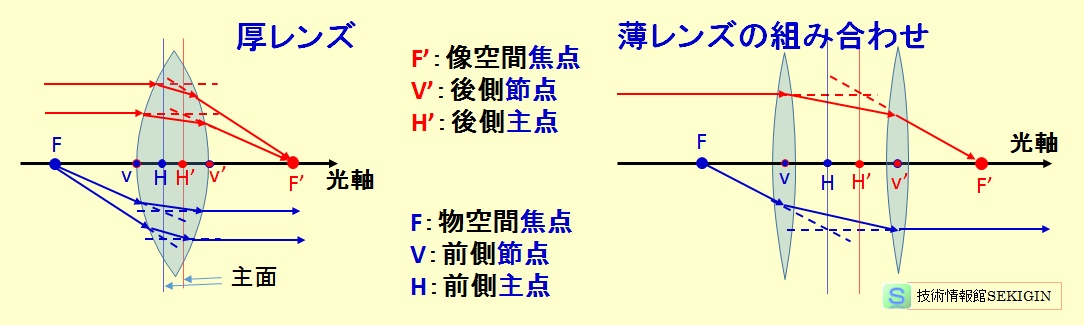
凸レンズの構造(模式図)
2 枚の薄レンズを組み合わせた場合,薄レンズ 1 の焦点距離 f 1 ,薄レンズ 2 の焦点距離 f 2 で,2 枚のレンズの間隔 d とした時,組み合わせレンズの焦点距離 F は,
で与えられる。
薄レンズの間隔を近づけ,接触( d ≒ 0 )させると,1 枚のレンズと同等に扱える。
図に示すように,焦点 F より外側(レンズから離れる)に物体を置くと,レンズの反対側に倒立像(実像)が得られる。
一方,図右のように,焦点 F より内側に物体を置いた場合(天眼鏡による拡大)は,レンズの反対側に実像が得られず,光線の逆向きの延長線上にあたかも正立像(虚像)があるように見える。この時の拡大倍率 m = | b/ a | は常に 1 より大きい。
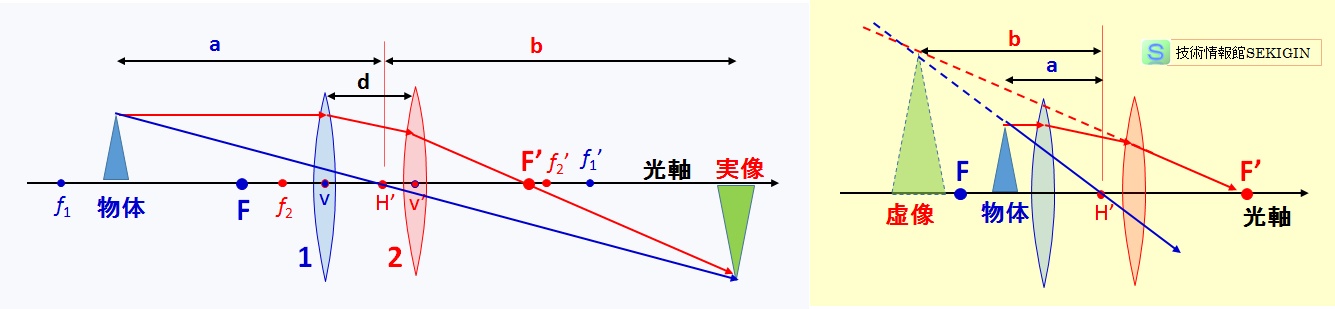
組み合わせレンズの焦点(模式図)
次には,代表的な組み合わせレンズの例として,主要な接眼レンズ(ocular)を紹介する。
ハイゲンス(ホイヘンス,Huygens,略号H )
片面凸,他の面が平面の大小 2 枚のレンズを組み合わせた 2 群 2 枚の接眼レンズ。
ラムスデン(Ramsden,略号R )
片面凸,他面が平面の2枚のレンズを凸面が向かい合うように組み合わせた 2 群 2枚の接眼レンズ。
プレスル(Plössl,略号PL )
ケルナー式の改良としてルーペ用の 2 群 4 枚の形式のレンズ。アッベ式同様に光学性能が高く,接眼レンズとして汎用される種類。
ケルナー(Kellner,略号K )
顕微鏡用に開発された 2 群 3 枚の接眼レンズ。
ナグラー(Nagler )
超広視界の接眼レンズ。
エルフレ(Erfle,略号E,Er )
1918年に軍用双眼鏡用として開発された。広視界が得られる 3 群 5 枚の接眼レンズ。
アッベ(Abbe,略号A )
顕微鏡用に開発された接眼レンズ。高い光学性能を有するので,オルソスコピック(整った像の意味,Orthoscopic,略号Or , OR , O )とも称されている。
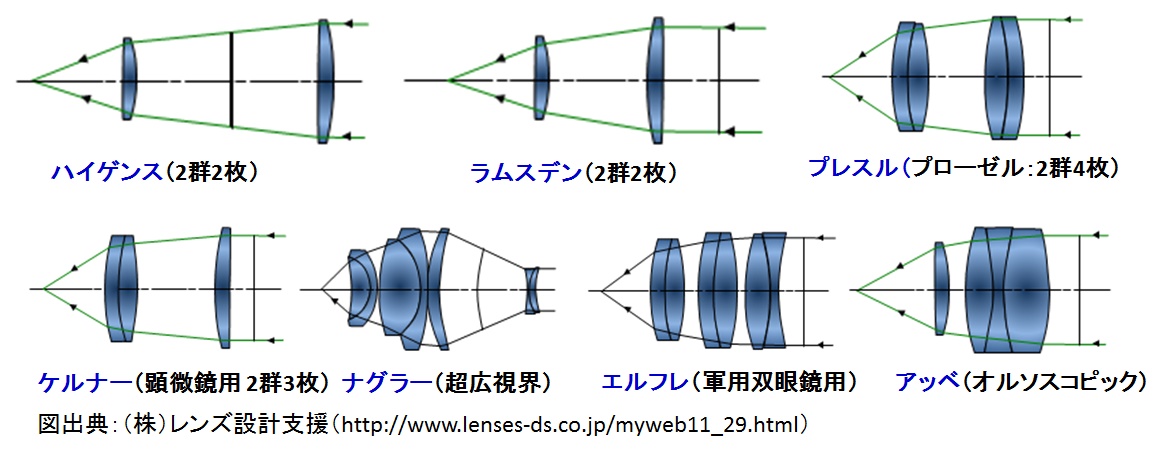
レンズ系の例(接眼レンズ)
元図出典:(株)レンズ設計支援
ページの先頭へ
【幾何光学関連の基礎用語】
- 入射角(angle of incidence , incident angle)
JIS Z 8120 (光学用語)の定義では,光が媒質の境界面に入射するとき,入射光線が入射点における境界面の法線となす角(鋭角)。 - 反射角(angle of reflection)
JIS Z 8120 (光学用語)の定義では,光が媒質の境界面に入射するとき,反射光線が入射点における境界面の法線となす角(鋭角)。 - 相対屈折率(index of relative refraction)
対象とする物質と,それを取り囲む物質との間の屈折率の比をいう。 - ホイヘンスの原理(Huygens’ principle)
オランダの物理学者ホイヘンスが唱えた波の伝播に関する仮説である。
『注目するある瞬間の波面上のすべての点が新しい波原となり,同じ速さ,同じ振動数の二次波(素元波;elementary wave)が球面波として送り出される。個々の素元波を観察することはできないが,全ての素元波に接する曲面(包絡面:envelopment surface)が,その時刻の波面として観察される。この現象が次々と起こり波面が波の進行方向に進む。』
ホイヘンスの原理は,ホイヘンス‐フレネルの原理(Huygens–Fresnel principle)ともよばれる。 - ホイヘンス(Christiaan Huygens)
クリスティアーン・ホイヘンス(1629年~1695年)は,オランダの数学者,物理学者,天文学者,1690年に光の波動説を提唱する『Traite de la lumiere:光についての論考』を発刊。 - スネルの法則(Snell's law)
屈折の法則(laws of refraction),デカルトの法則(Descartes' law)ともいわれ,光が二つの媒質の境界面で屈折するとき,入射角の正弦と屈折角の正弦との比(屈折率)は一定で,その値は二つの媒質のみによって定まるという法則。
オランダの天文学者スネルが発見し,フランスの哲学者デカルトがまとめた法則である。 - スネル(Willebrord Snell)
ヴィレブロルト・スネル(1580年~ 1626年)は,オランダの天文学者,数学者でスネルの法則(光の屈折)で知られる。 - 素元波(elementary wave)
ホイヘンスの原理における前進する波面の各点から出る小さな無数の球面波。 - 包絡面(envelopment surface)
空間内の曲面群のすべてに接する曲面を,曲面群の包絡面という。 - 波面(wave front)
空間を波動が伝わるとき,その位相の等しい点を連ねた面をいう。
JIS Z 8120 (光学用語)の定義では,光波が伝搬するときの同一位相面(等位相面)。 - 球面波(spherical wave)
三次元の等方媒質中において,ある一点(波源)を中心とし,放射状に広がる波,又はある一点に向かって収束する波で,球対称の波となる。なお,波源から遠ざかると,球面は平面に近づき,遂に平面波になる。 - 平面波(plane wave)
波面が波の進行方向に垂直な平面上にある波をいう。波源からきわめて遠く離れている球面波は近似的に平面波とみなすことができる。 - 点光源(point source , positional light source)
JIS Z 8120 (光学用語)の定義では,その大きさが放射(又は光)を受ける面までの距離に比べて十分小さく,計算及び測定に際して大きさを無視できる放射源(又は光源)。 - 物点(object point)
JIS Z 8120 (光学用語)の定義では,物体空間における物体の一点。これは理想的な点光源とみなされる。 - 像点(image point)
JIS Z 8120 (光学用語)の定義では,光学系の物点から出る共心光線束が,像空間において収束する点,又は共心光線束を光線の進む方向と反対の方向に延長したとき像空間において収束する点。 - 像面(image surface)
JIS Z 8120 (光学用語)の定義では,
a) 光学系の物体面から出る共心光線束によって像が生じる面。すなわち,物体面と共役な面。
b) 像空間において像を表す面。通常は平面で表す。 - 像空間(image space)
JIS Z 8120 (光学用語)の定義では,光学系の結像において,光線が入射する側の空間(屈折率 n)と,射出する側の空間(屈折率 n')とを考えるとき,屈折率 n'を用いて表される空間。 - 実像(real image)
JIS Z 8120 (光学用語)の定義では,光学系の射出面から出た収束光線束が,像空間で結ぶ像。 - 虚像(virtual image)
JIS Z 8120 (光学用語)の定義では,光学系の射出面から出た発散光線束が,像空間で結ぶ像。 - 収束光線束(convergent pencil of rays)
JIS Z 8120 (光学用語)の定義では,一点に向かって収束する光線束。 - 発散光線束(divergent pencil of rays)
JIS Z 8120 (光学用語)の定義では,一点から発散する光線束。 - 収差(aberration)
JIS Z 8120 (光学用語)の定義では,光学系によって結像する場合,像の理想像からの幾何光学的なずれ。球面収差,コマ収差,非点収差,像面の湾曲,ディストーション,色収差などがある。 - 対物レンズ(objective)
JIS Z 8120 (光学用語)の定義では,光学器械において物体を最初に結像する光学系。望遠鏡においては反射を利用するものを対物鏡という。 - 接眼レンズ(eyepiece , ocular)
JIS Z 8120 (光学用語)の定義では,望遠鏡,顕微鏡などで対物レンズによる像を拡大して見るためのレンズ。
ページの先頭へ