物理 第二部:古典力学の基礎
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
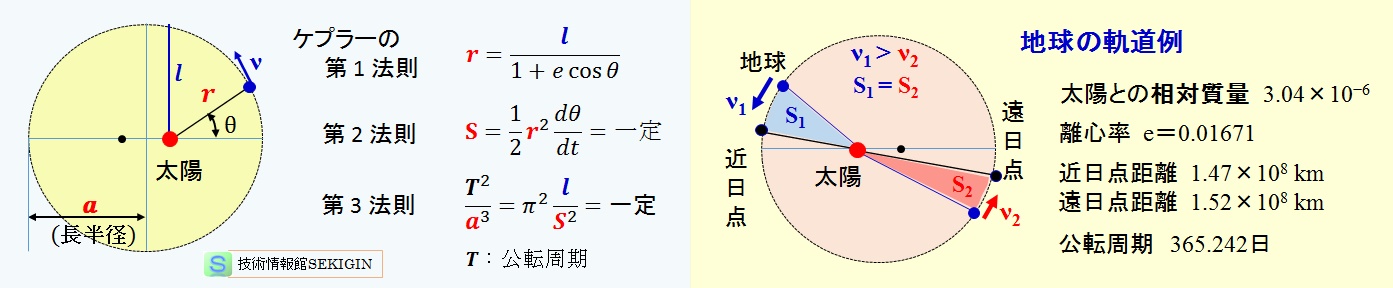
ここでは,最も身近な惑星の運動に関連し, 【楕円軌道】, 【ケプラーの法則】, 【万有引力】 に項目を分けて紹介する。
【楕円軌道】
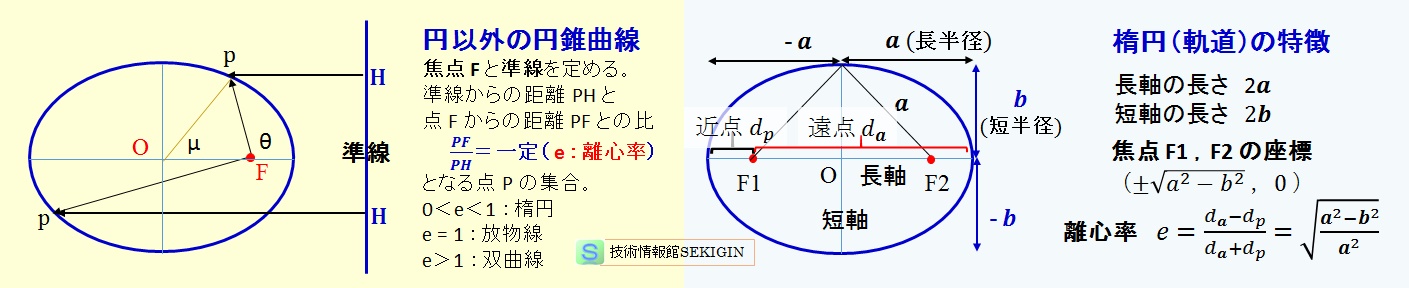
楕円(ellipse)は,円錐曲線(conic curve)の一種である。
円錐曲線とは,円錐を切断したときの断面として得られる曲線で,円錐の底面に並行な平面で切断した円(circle),底面に並行でない平面で切断した楕円(ellipse),円錐の母線に平行な平面で切断した放物線(parabola),母線に並行でない平面で切断した双曲線(hyperbola)に分けられる。
円錐曲線を描く場合は,直線(準線)と直線上に含まれない点 F (焦点)を定め,準線上の点 H を動かしながら,点 H から準線に垂直な直線上に,PF/ PH =一定( e > 0 )となる点 P の集合として得られる。
PF と PH の比 e を離心率(eccentricity)といい,円錐曲線の特徴を示す数値のひとつである。離心率 e の値により,描かれる円錐曲線の概形が楕円( 0 < e < 1 ),放物線( e = 1 ),双曲線( e > 1 )となる。
なお,この方法では,円を描くことができないが,準線と焦点を無限に離したと仮定した時に円になると考え,数学的には,便宜上 e = 0 のとき円が描かれるとする。
既に描かれた楕円の離心率は,図のように,焦点からの近点,遠点,又は楕円の長半径,短半径から求められる。
楕円の特徴
楕円軌道とは,楕円形の軌道をいう。点 P の軌道は,焦点 F を極とし,線分 PF の長さ 𝒓 とX軸と成す角度をθとした時,極座標平面 ( 𝒓 , θ ) で,
で表される。
なお,e は離心率,𝑙 は焦点 F から準線までの距離に離心率 e を掛けたもので,半直弦(semi-latus rectum)や半通径と呼ばれる。
半直弦( 𝑙 ),離心率( e ),長半径( 𝒂 ),短半径( 𝒃 )とには次の関係がある。
平面極座標を長軸と短軸の交点 O を極とした場合と焦点 F を極とした場合とには,
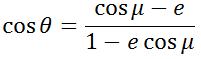
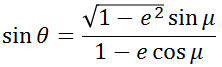
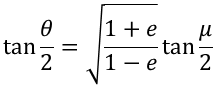
の関係がある。
なお,極座標平面( 𝒓 , θ)から直交直線座標( x , y )への変換は,
で与えられる。
【参考:基礎用語】
- 円錐曲線(conic curve)
円錐切断曲線,二次曲線ともいわれる。双方に無限に伸びた直円錐(頂点と底面を結ぶ中心線が底面に垂直な円錐)の頂点を通らない平面で切りとった時の切り口の曲線をいう。
平面の傾きで,円,楕円,放物線,双曲線が得られる。これらの曲線は二次方程式と対応させられるので二次曲線ともいわれる。 - 円(circle)
円錐曲線の一つで,平面上の定点から一定の距離にある軌跡をいう。この定点を円の中心,一定の距離を半径という。
軌跡の内部全体を含めて円というときは,軌跡は円周と呼ばれる。 - 楕円(ellipse)
円錐曲線の一つで,長円ともいわれ,平面上の 2 つの定点からの距離の和が一定となる軌跡をいう。 2 つの定点は,楕円の焦点と呼ばれる。 - 放物線(parabola)
円錐曲線の一つで,平面上で一つの直線までの距離と直線上にない定点までの距離が等しい点の軌跡をいう。
定点を放物線の焦点,直線を放物線の準線という。なお,放物線は準線に垂直で焦点を通る軸に対して対称となる。 - 双曲線(hyperbola)
円錐曲線の一つで,平面上で 2 つの定点からの距離の差が正の定数となる点の軌跡をいう。2 つの定点を双曲線の焦点という。 - 離心率(eccentricity)
円錐曲線の形を決める定数で,2 つの焦点間の距離を正の定数で除した値をいう。1より小さければ楕円,1 に等しければ放物線,1 より大きければ双曲線になる。 - 極座標系(polar coordinates system)
空間上の点を表す方法の一つで,n 次元ユークリッド空間では,1 個の動径と n − 1 個の偏角からなる座標系である。
平面(二次元)上の点の場合(極座標平面)では,定点 O からの距離 r と定半直線(動径)からの偏角θとによって座標( r ,θ)と表す。直交直線座標( x , y )とは,x = cos θ,y = sin θの関係がある。 - 直交座標系(rectangular coordinate system)
空間上の点を表す方法の一つで,互いに直交している座標軸を指定することで定まる座標系である。
平面(二次元)上の点の場合(直交直線座標)では,平面上で直角に交わる二直線( X軸,Y軸)を定めて座標( x , y )と表す。極座標平面( r ,θ)とは,x = cos θ,y = sin θの関係がある。 - ケプラー(Johannes Kepler)
ヨハネス・ケプラー(1571年 ~ 1630年)は,ドイツの天文学者で,天体の運行法則を唱え,理論的に天体の運動を解明したことで知られる。天体物理学の先駆的存在といわれている。 - 中心力(central force)
向心力とは定義が異なり,原点(定点)と物体を結ぶ線に沿って,原点と物体との距離 𝒓 にのみ依存する力,運動する物体相互を結ぶ線に沿って,物体間の距離で一義的に決まる力で,万有引力やクーロン力などがこれに相当する。
ページの先頭へ
【ケプラーの法則】
ケプラーの法則(Kepler's laws)
ヨハネス・ケプラーが発見し惑星の運動に関する法則。過去の観測記録などから太陽に対する火星の運動を定式化した次の 3 つの法則をいう。
第1法則(楕円軌道の法則:1609年):“惑星は,太陽をひとつの焦点とする楕円軌道上を動く。”
楕円軌道は,2 つの焦点を持ち,離心率 0< e <1 の円錐曲線を描く軌道である。
惑星の軌道は太陽の位置を焦点とし,軌道の半直弦 l ,離心率 e ,長半径 𝒂 のとき,
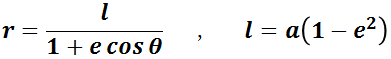
で表される。
第2法則(面積速度一定の法則:1609年):“惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である(面積速度一定)。”
例えば,下図の例の様に,地球の公転の速度(平均軌道速度 29.78 km/s )が太陽から離れるほど早くなるため,単位時間に太陽を結ぶ線分(動径という)が描く面積(面積速度 S )は等しくなる。なお,面積速度 S は,惑星により異なるが,惑星に固有の一定値である。
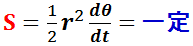
第3法則(調和の法則:1619年):“惑星の公転周期 T の 2 乗は,軌道の長半径 𝒂 の 3 乗に比例する。”
すなわち,惑星によらず,
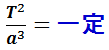
半直弦と面積速度の関係
ここで,長半径 𝒂 ,短半径 b のとき,楕円の面積は,π𝒂 b で与えられるので,公転周期 T は,楕円の面積と面積速度 S とから
![]()
で得られる。ここで,長半径,短半径,半直弦 l ,離心率 e の関係
![]()
から得られる長半径 𝒂 と公転周期 T の関係と第 3 法則により
![]()
が得られる。
従って,半直弦と面積速度について,惑星によらず
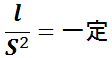
の関係が導かれる。
ケプラーの法則は,太陽と惑星に関して論じているが,この法則は惑星と衛星(あるいは人工衛星)などの間でも成立する。
地球の軌道の特徴
ページの先頭へ
【万有引力】
ニュートンは,太陽を公転する地球の運動や木星の衛星の運動の説明を試み,ケプラーの法則に運動方程式を適用し,引力(重力)が 2 つの物体の質量(重力質量)に比例し,距離の2乗に反比例(万有引力の法則:law of universal gravitation)することを証明した。
極座標における力 F は,焦点と質点を結ぶ線分方向( 𝒓 方向)とそれに垂直の線分の角度を増す方向(θ方向)に分けて考えられる。
F = F𝒓+Fθ
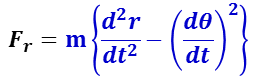
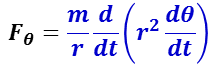
ここで,ケプラーの第 2 法則を適用すると,
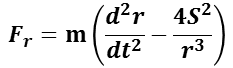
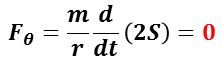
となり,質点(惑星)に作用する力は,焦点(太陽)との線分に沿ったstrong>力であることが分かる。
ここで,ケプラーの第 1 法則の t での微分と,第 2 法則とから,
![]()
が得られ,これの微分とケプラーの第 1 法則,第 2 法則とから
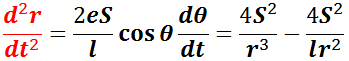
が得られるので,これを代入すると, F𝒓 は,
![]()
となる。この力は,焦点に向かい,距離のみに依存するので,向心力ではなく中心力であることが分かる。
ここで,ケプラーの第 3 法則から得られた半直弦と面積速度の関係により,惑星の種類によらない定数 C を用いて,
![]()
と書ける。この関係は,惑星に注目した力であるが,作用反作用の法則から質量 M の太陽にも作用すると考えられるので,この力は,
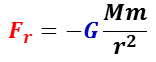
と書き換えられる。比例定数 G は,太陽,惑星に関与しない普遍的定数となる。
これを一般化した法則が万有引力の法則である。
比例定数 G を万有引力定数(重力定数)といい, CODATA(科学技術データ委員会: Committee on Data for Science and Technology)の2014年の推奨値は,G = 6.674 08(31)×10-11(Nm2kg-2)である。
ページの先頭へ