物理 第三部：流体の物理

　一般的には，流体が運動するとき，ある面に垂直に作用する垂直応力（normal stress）の他に，流体の内部摩擦により，面と平行な接線応力（tangential stress）が現れる。この応力が現れる現象を粘性（viscosity）といい，粘性が無視できない流体を粘性流体（viscous fluid），粘性を無視した取扱いができる仮想的な流体を完全流体（perfect fluid）という。
　
　圧力について
　運動している完全流体を問題とする場合は，例えば，静止流体の圧力の説明で用いた三角錐の加速度 dμ/ dt を考慮しなければならない。
　従って，流体の密度ρ，重力加速度 g ，三角錐の体積 V ＝ (OA×OB×OC)÷6 ）とし，面△ABC の外向きの法線の方向余弦（direction cosine）を（ l , m , n ）としたとき，直交座標系（x，y，z）の各成分の力のつり合いは，接線応力が無視されるので，圧力（ p ）と運動方向の力（ρV･dμ/ dt ）とのつり合いになる。
　X 軸方向の力の釣り合い
　　　　　　　p_x △OBC － p △ABC×l ＝ ρV ･ dμ_x / dt
　Y 軸方向の力の釣り合い
　　　　　　　p_y △OCA － p △ABC×m ＝ρV ･ dμ_y / dt
　Z 軸方向の力の釣り合い
　　　　　　　p_z △OAB － p △ABC×n － ρg V ＝ρV ･ dμ_z / dt
　
　静止流体の圧力での説明と同様に，三角錐のOA ，OB ，OC を限りなく小さくしてゆくと，三角錐の体積が無視できるほどに限りなく小さくなるので，点 O での圧力の大きさは，想定した 4 つの面の選び方（方向）に関係なく，静止流体の圧力と同様に
　　　　　　　p_x ＝ p_y ＝ p_z ＝ p
の関係が得られる。

　完全流体の運動
　運動する完全流体の中にある点に注目すると，その点の圧力は方向に関係なく同じである。しかし，流れの中では，完全流体の各部はそれぞれの速度で運動している。
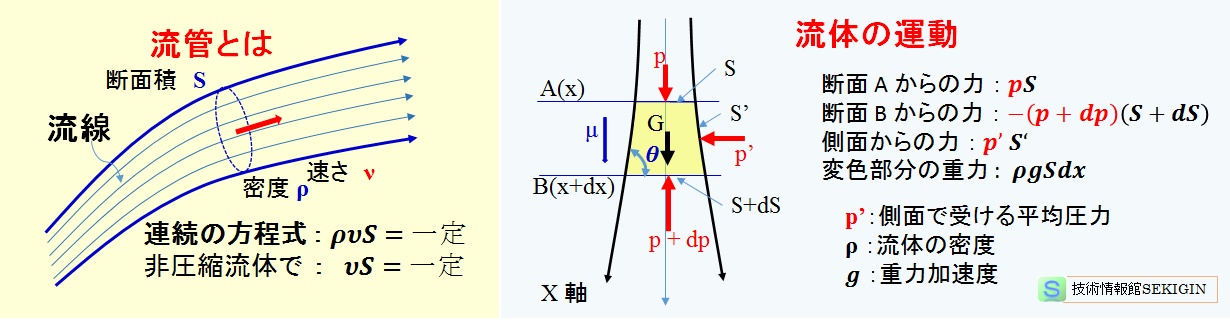
　そこで，ある瞬間に注目し，各部の速度を矢印で示すと，矢印の始点と終点がつながった，すなわち速度ベクトルを接線とする曲線を描く。この曲線を流線（streamline）といい，隣接した流線の束を流管（stream tube）という。
　
　流管の中のある点を採った時，その点での流速が時間と共に変化しない流れを定常流（steady flow）という。
　定常流の中に一つの流管を考えた時，その中の任意の点における速さν，流管の断面積 S ，流体の密度ρとした時，単位時間にその点を通過する流体の質量が変わらないので，
　　　　　　　ρ ν S ＝一定
の関係が得られる。これを連続の方程式という。
　なお，流体が液体のように，圧力が変わっても密度変化の非常に小さい非圧縮性流体（incompressible fluid）では，
　　　　　　　ν S ＝一定
と書ける。 　【参考：基礎用語】

• 粘性（viscosity）
  　流れの速さの違いをならして一様にしようとする流体の性質をいう。
  　流体内部に速度勾配があるとき，速度を一様にするような向きの接線応力（内部摩擦）が現れる。この力を粘性力といい，粘性を示す流体を粘性流体という。
  　粘性力が速度勾配に比例するとき，この流体をニュートン流体という。ニュートン流体の単位面積あたりの粘性力と速度勾配との比を粘性係数（粘性率）という。
• ニュートンの粘性法則（Newton's law of viscosity）
  　ニュートンの応力公式とも呼ばれる法則で，流体のずれ応力，せん断応力などとも呼ばれる接線応力は速度勾配に比例する。
• 粘性係数（coefficient of viscosity）
  　粘性率，粘度ともいわれる流体の粘性の大きさを表わす定数。粘性流体の変形の応力と変形速度の比で表される。
• 方向余弦（direction cosine）
  　空間に直交座標系（x，y，z）があるとき，有向直線（ベクトル）が X ，Y ，Z 軸の正の向きとの“はさむ角”をそれぞれα，β，γとすると，l ＝ cos α，m ＝ cosβ，n ＝ cosγをその直線の方向余弦という。
• オイラー（Leonhard Euler）
  　レオンハルト・オイラー（1707年～1783年）は，ロシア・ドイツの数学者・天文学者（天体物理学者）で，オイラーの公式，オイラーの等式，オイラー積分など，微分積分の創始以来で，解析学の技法的な完成に寄与した。
• 体積力（volume force; body force）
  　重力や浮力など物体に働く力が物体の体積に比例するものを指す。流体力学や材料力学において，粘性力や弾性力などの表面力に対して用いられる。
• ベルヌーイ（Daniel Bernoulli）
  　ダニエル・ベルヌーイ（1700年～1782年）は，スイスの数学者・物理学者。1738年に『流体力学』を出版。ベルヌーイの定理「空気や水の流れがはやくなると，そのはやくなった部分は圧力が低くなる。はやく流れるほど圧力は下がる。」など，流体力学の基礎を築いた。
• 動粘性係数（kinematic viscosity）
  　動粘度，動粘性率ともいい，粘性率を密度で割った値で，流体の粘性の度合いを示す。
• ニュートンの粘性法則（Newton's law of viscosity）
  　ニュートンの応力公式とも呼ばれる法則で，流体のずれ応力，せん断応力などとも呼ばれる接線応力は速度勾配に比例する。
  　別の表現では，流体の速度が流れに垂直な方向に変化しているとき，流れに平行な面が受ける粘性力（接線応力）は垂直な方向の速度変化率（速度勾配）に比例する。これを満足するような流体をニュートン流体といい，比例係数を粘性率という。
  　ナビエ＝ストークス方程式では，この法則は応力テンソルと変形速度テンソルの比例関係に置き換えられている。
• ニュートンの流体摩擦法則（Newton's friction law）
  　ニュートン流体では，流体におけるずり応力は，速度勾配に比例する。

　簡単のため，上図に示した X 軸を鉛直下方にとり，これに沿う細い流管を考える。ここで，X 軸に垂直の近接した断面 A （ x ），B（ x + dx ） を採り，それらの断面積を S ，S＋dS とする。
　断面 A ，B 間（図中の着色領域）の完全流体に作用する力は，
　　　　　　　断面 A からの力 ： 圧力（ p ）× 断面積（ S ）
　　　　　　　断面 B からの力 ： 圧力（ －(p＋dp) ）× 断面積（ S＋dS ）
　　　　　　　側面からの力 ： 側面で受ける平均圧力（ p’）× 側面積（ S’）
　側面からの力の X 成分は，側面と断面 B との成す角θから，
　　　　　　　p’× S’cos θ
とできる。また，断面 B の断面積の増加分 dS ＝ S’cos θ とでき，平均圧 p’を断面 A と B の圧力の中間の値，すなわち p より微小量（Δp ）だけ大きいとする。
　これにより，流体の密度ρ，流速μとすると流体の運動方程式は，
　　　　　　　
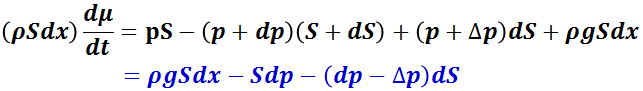
とかける。なお，ρ𝑔 S dx は，断面 A ，B 間の重力である。
　ここで (dp-∆p)dS の項が省略できるとする。また，p ( x , t ) のある瞬間に注目しての値であることを考慮し，
　　　　　　　
と書ける。
　これは一次元の場合を示すが，同様の考え方で三次元の場合も導くことができる。
　dμ/ dt は，ある点を通るときの速度μ ( x , t) の変化を意味せずに，図中の注目領域を追いかけながら見た時の値であるので，これを明瞭にするため，一般的には，重力のような体積力 f を用いて，
　　　　　　　
と表され，オイラーの流体運動方程式（Euler's equation of fluid motion）と呼ばれる。

　ベルヌーイの定理（Bernoulli's theorem）により流体の挙動を平易に表すことができ，力学的エネルギー保存則に相当する定理である。
　ベルヌーイの式は，完全流体の速さと圧力と外力のポテンシャルの関係を記述する式であるが，完全流体でなくともわずかな修正で成立する場合が多く，ベンチュリ管やピトー管による流速測定の原理などの応用が多岐にわたる。
　
　ベルヌーイの式は，外力が保存力であること，密度が圧力のみの関数となるバルトロピー流体であることに加えて，適用する非粘性流体の分類に応じて，定常流の条件で成り立つものと，渦なしの流れの条件で成り立つものに分けられる。
　なお，定常流とは，すべての点における速度，圧力，密度などが時間的に変化しない流れをいう。
　
　定常流におけるベルヌーイの定理
　外力が保存力で，非粘性のバルトロピー流体の定常な流れで，速度ベクトルν，圧力 p ，密度ρ，外力 f のポテンシャルΩ（ f =－∇Ω）としたとき，
　　　　　　　
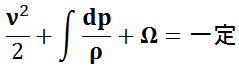
が流線上のみで成り立つ。
　一様な重力場で，重力加速度の大きさ g ，鉛直方向の座標 z とすると，
　　　　　　　
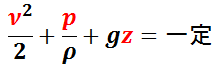
と書ける。
　
　渦なし流におけるベルヌーイの定理
　外力が保存力，非粘性のバルトロピー流体の渦なしの流れで全空間において成り立つ一般的な式である。
　速度ポテンシャル（Velocity potential）φが存在し，速さ v = ∇φと表せ，任意の関数 f (t) としたとき，圧力方程式
　　　　　　　
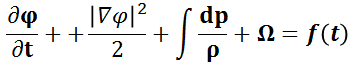
が成り立つ。

　速度ポテンシャル
　流体力学で，渦なし流れの解析に用いられる。渦なし流においては，速度ベクトルを u ，渦度ベクトルを ω とすると，ω＝rot u ＝ 0 であるから，関数の値がスカラー値を取る適当なスカラー関数φを用いて，u ＝grad φと書ける。このφを速度ポテンシャル（velocity potential）という。
　特に非圧縮性流体においては，連続の方程式 div u ＝0 から，△φ＝0 ( △ はラプラシアン ) となる。すなわち，速度ポテンシャル φ は調和関数であり，境界条件を満たす調和関数φが決れば，流れの速度場 u はただちに決定される。
　
　調和関数（harmonic function）
　2つの実変数 x ，y の実関数 u (x，y) が，ある領域内で連続かつ1次および2次の偏導関数をもち，2次元のラプラスの方程式 Δu＝∂²u/∂x²＋∂²u/∂y²＝0 を満たすとき，この関数 u (x，y) はその領域において調和であるといい，u (x，y) を調和関数と呼ぶ。
　調和関数は，n 次元空間内の領域で定義された関数についても，n 次元のラプラスの方程式を満足する関数として，同様に定義する。
　ラプラシアン（laplacian ，Δ）
　三次元空間において，微分演算子 Δ＝∂2/∂x2＋∂2/∂y2＋∂2/∂z2 をラプラシアンまたはラプラス演算子という。
　微分演算子ナブラ ∇ ，ダイバージェンス div ，グラジエント grad を用いると，ラプラシアンはΔ＝∇・∇＝div grad と書くことができる。
　ナブラ（nabla ，∇）
　三次元直交座標 x ，y ，z について，各成分が ∂/∂x ，∂/∂y ，∂/∂z で表わされるベクトルをナブラといい，∇ という記号で表わす。
　∇＝(∂/∂x，∂/∂y，∂/∂z) を使うと，ベクトル場 u＝(ux，uy，uz) において，グラジエントは grad φ＝∇φ ，ダイバージェンスは div u＝∇・u (スカラー積) ，ローテーションは rot u＝∇×u （ベクトル積）と表わされる。
　また ∇ 自身のスカラー積（∇・∇）をとると，ラプラシアン Δである。
　ダイバージェンス（divergence ，div）
　ベクトル場 u＝(ux，uy，uz) において，div u＝∂ux/∂x＋∂uy/∂y＋∂uz/∂z で定義されるスカラー div u を u のダイバージェンスまたは発散という。
　また微分演算子ナブラ ∇＝(∂/∂x，∂/∂y，∂/∂z) と u とのスカラー積と考えて，div u＝∇・u と表わすこともできる。
　グラジエント（gradient ，grad）
　スカラー場 f において，∂f/∂x，∂f/∂y，∂f/∂z を成分とするベクトルを grad f と書き，f のグラジエントまたは勾配という。
　ナブラ ∇＝(∂/∂x，∂/∂y，∂/∂z) という微分演算子を用いると，grad f＝∇ f と表すことができる。グラジエントは，スカラーポテンシャルを考えるときに必要になる。
　ローテーション（rotation ，rot）
　ベクトル場 u＝(ux，uy，uz) において，∂uz/∂y－∂uy/∂z，∂ux/∂z－∂uz/∂x，∂uy/∂x－∂ux/∂y を成分とするベクトルを rot u と書き，u のローテーションや回転といい，curl uと書くこともある。ベクトル u は物体内部の各点の変位を表し，rot u は各部分の回転を表わす。
　微分演算子ナブラ ∇＝(∂/∂x，∂/∂y，∂/∂z) と u とのベクトル積を用いて，rot u＝∇×u と表わすことができる。
　スカラーポテンシャル（scalar potential）
　ベクトル場 u＝(ux，uy，uz) が rot u＝0 という条件を満足しているとき，u＝－grad φを満足するスカラー場φが存在する。このφを u のスカラーポテンシャルという。
　さらに div u＝ 0 であれば，φはラプラス方程式を満足する。

　ナビエ–ストークス方程式（Navier–Stokes equations）は，粘性流体の運動を記述する2階非線型偏微分方程式で，NS 方程式とも略され，運動量の流れの保存則を表す。
　
　ナビエ–ストークス方程式は，そのままで解を求めることが困難なほど複雑である。粘性率が一定で非圧縮性の流れに関し，流れの速度場 v ，密度ρ，圧力 p ，動粘性係数ν（=μ/ρ）， 外力場（加速度）f とした時，近似方程式は，
　　　　　　　
で与えられる。
　これは，前出のオイラーの流体運動方程式と比べて，右辺に動粘性係数（kinematic viscosity）の掛かった項が加えられているだけである。
　この式を用いて得られる解は，単純な層流の場合に限られ，日常生活で観察される流れにはコンピュータを用いた数値計算が必要となる。
　
　ナビエ–ストークス方程式は，空間の中の流体の運動を記述し，この解は多くの場面で応用されているが，方程式の理論的な理解は不完全である。
　特に，乱流となる場合には，科学的，工学的に非常に重要であるにもかかわらず，最も難しい未解決問題の一つとして残っている。

　粘性流体（viscous fluid）の運動について，理論的な考察で十分な答えを導くことが困難である。特に乱流を含む流れの解析では，実験結果などを基本にして単純なモデルに置き換えるなどの工夫がされる。
　
　粘性を有する流体の流れでは，粘性による影響を強く受ける物体表面近傍の境界層を考慮しなければならない。
　程度の差はあるが，すべての流体は粘性を有する。流体の一様な流れ（一様流）の中に，物体を置いた場合に，物体表面の流速はゼロで，物体表面から離れるに従い流速が増し，遂には一様流と同じ速度になる。物体表面から一様流と同じ流速になるまで，流速が変化する流体の層を境界層という。
　静止した流体中で物体を動かした場合も同様に，物体表面付近の流体の層を境界層という。
　
　境界層（boundary layer）
　流体の粘性が大きいほど厚くなり，流体の運動を考察する際には，境界層の外側では完全流体の理論を適用できるが，内側では粘性を考慮した取扱いを必要とする。
　物体が流体中を動くとき受ける抵抗には，境界層内の粘性によって引き起こされる摩擦力（skin friction）がある。
　円柱や球のような物体の場合は，物体表面に働く圧力勾配により，境界層内で発生した逆流により，物体表面からの境界層のはがれにより，物体の後ろに渦の層ができる。
　この渦は，次々に分裂して複雑な乱流の原因になる。このような場合には，物体の前後で圧力差が生じ，摩擦力以外に圧力抵抗（pressure drag）も受けることになる。
　
　境界層の厚さ分類
　99 ％境界層厚さ（ 99％boundary layer thickness）
　境界層の厚さそのものを表そうとするもので，壁から外側の速度（ポテンシャル流の 速度）U_∞ の 99 ％の値をとる位置までの長さで定義。通常は，記号δが使われる。
　排除厚さ（displacement thickness）
　ポテンシャル流の速度があるべきところが粘性により速度が減少したために，流れが外側に押 しやられ，あるいは排除された形になる。従って，物体表面が外側に出っ張ることと等価になる。この排除された量は，横軸を一様流の速度としたときに，どのくらいの高さに相当する量かで換算して定義する。通常は，記号δ₁ やδ^* が使われる。
　排除厚さ δ₁ は，99 ％境界層厚さδの約1/ 3 の大きさである｡
　運動量厚さ（momentum thickness）
　ポテンシャル流れに対する運動量の損失を意味し，もしポテンシャル流が壁まで存在していると考えた場合の失われた運動量が，一様流の運動量に換算してどのくらいの量になるかを高さで表す。通常は，記号δ₂ やθが使われる。
　運動量厚さδ₂ は，排除厚さδ₁の約 1/ 3 の大きさである。

　粘性流体の運動では，粘性によるせん断応力（接線応力），壁面上での non-slip 条件を考慮しなければならない。
　
　粘性による影響
　下図は壁面と平行に流れる単純な流れの流速分布を示したものである。壁面の方向にX 軸，壁面と鉛直方向に Y 軸をとり，壁面からの距離に伴う流体の流れ（速度分布）を示したものである。
　壁面の表面，すなわち y = 0 の流速が 0 で，壁面から離れるとともに流速が大きくなり，壁面からの距離が前出の境界層を超えると距離に関わらず流速は一定になる。
　
　non-slip 条件
　壁面上を流れる場合，流体粒子のような非常に小さな粒子（分子や会合した分子など）は，壁面との界面では物理的あるいは化学的に吸着（adsorption）する。
　壁面界面に吸着した流体粒子は，容易に移動できないため，壁面上の流速は 0 と考えられる。これを粘性流体の non－slip 条件と呼ぶ。
　吸着とは
　壁面と流体の界面において，壁面表面の原子は，壁材の内部とは異なり，周囲と結合していない部分を有し，自由エネルギーが大きくなる（界面自由エネルギー）。
　このため，壁面表面の原子は，界面自由エネルギーーを小さくするため，近接した分子などの化学種と結合する。この現象を吸着といい，結合様式により，ファンデルワールス力による物理吸着，共有結合やイオン結合による化学吸着に分けられる。
　
　せん断応力
　粘性流体では，流体粒子間に，流れと同じ方向（接線方向）に 粘性によるせん断応力（接線応力）が作用する。
　ニュー トンはこのせん断応力が流速ベクトルと垂直な方向への速度勾配（せん断変形速度）に比例すると仮定した。
　このため，流体のせん断応力とせん断変形速度（流れの速度勾配，ずり速度ともいう）に比例関係があるとき，その流体はニュートン流体（Newtonian fluid）といい，比例関係にない流体を非ニュートン流体という。
　
　ニュートンの仮定
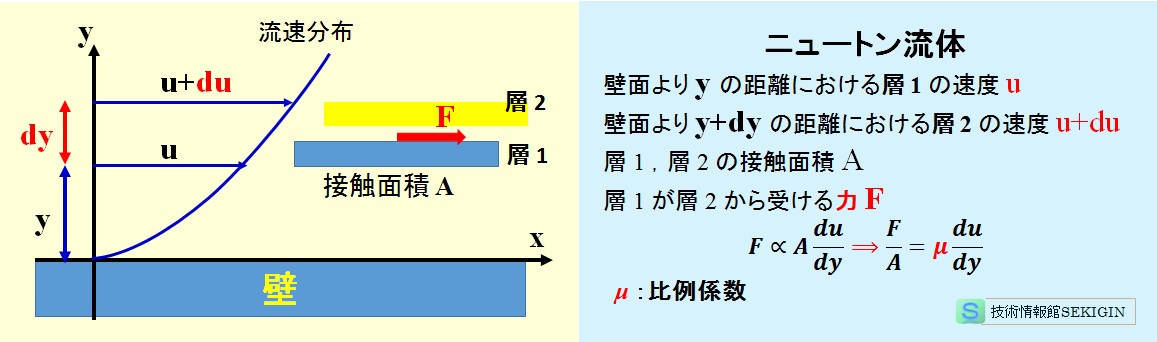
　下図に示すように，壁面の方向にX 軸，壁面と鉛直方向に Y 軸をとり，壁面からの距離に伴う流体の流れ（速度分布）は，壁面の表面，すなわち y = 0 の流速が 0 で，壁面から離れるとともに流速が大きくなる。
　壁面からの距離 y における流れの層 1 の速度を u ，壁面から距離 y＋dy の層 2 の速度を u＋du とする。この時，速度の大きい層 2 は，層 1 を X 軸方向に力 F で引っ張る。
　ニュートンは，この 2 層の接触面積を A とすると， 力 F は，接触面積 A ，速度の差 du に比例し，距離の差 dy に逆比例すると，
　　　　　　　F ∝ A･du/ dy
と仮定した。この式は，比例係数μを用いて，
　　　　　　　F/ A ＝μ･du/ dy
と書ける。
　この仮定（ニュートンの粘性法則やニュートンの流体摩擦法則ともいわれる）は，その後の実験などにより正しいことが認められ，この仮定に従う流体をニュートン流体と呼ばれた。
　F/ A は，単位面積当たりの接線方向の力なので，これをτで表すと，
　　　　　　　τ＝μ･du/ dy
となる。なお，τ はせん断応力（sheering stress），比例係数 μは粘性係数（coefficient of viscosity），粘性率，粘度と呼ばれる。粘性係数の記号としてη（エータ，イタ）を用いる文献も多い。
　粘性係数を密度ρで割ったν（=μ/ρ）は，動粘性係数（kinematic viscosity），動粘性率，動粘度などと呼ばれる。

　なお，非ニュートン流体には，せん断応力とせん断変形速度の関係により，擬塑性流体，ビンガム流体，ダイラタント流体などがある。