物理 第二部:古典力学の基礎
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,仕事とエネルギーの基本について, 【仕事とは】, 【仕事の原理,仕事率】, 【仕事の種類と単位】, 【エネルギーとは】 に項目を分けて紹介する。
【仕事とは】
仕事(work)とは,一般的には,何かを作り出す,又は成し遂げるための行動をいう。
物理学においては,力 F を受けた物体が,力の方向に x 移動(変位)した時に,ベクトルの力と変位の積(内積)を,その力のした仕事 W という。(ここでは,ベクトルを矢印付きではなく,太字で記す。)
W = F x
内積(inner product)とは,スカラー積ともいい,二つのベクトルの単位座標ベクトルに関する成分どうしの積の和(スカラー量)をいう。ベクトル a ,b のなす角をθとするとき,ab cosθを内積という。また,a =(a1, a2),b =(b1, b2)と成分表示した時は,内積はa1b1+a2b2となる。
従って,仕事は,
W = F x = F x cos θ
で表わされる。
氷上のストーンを投げて争うカーリングというゲームを例に仕事を考える。この時,氷とストーンの摩擦係数を ゼロと仮定する。
下図に示すように,一定の力 F でストーンを押している変位 x の間は等加速度直線運動で,ストーンを離した後は,等速直線運動となる。
物理学では,ストーンを押し続けている間に仕事をするといい,ストーンを離した後は,一定の速さで動き続けるが,どこまで移動しても仕事をしたとは言わない。
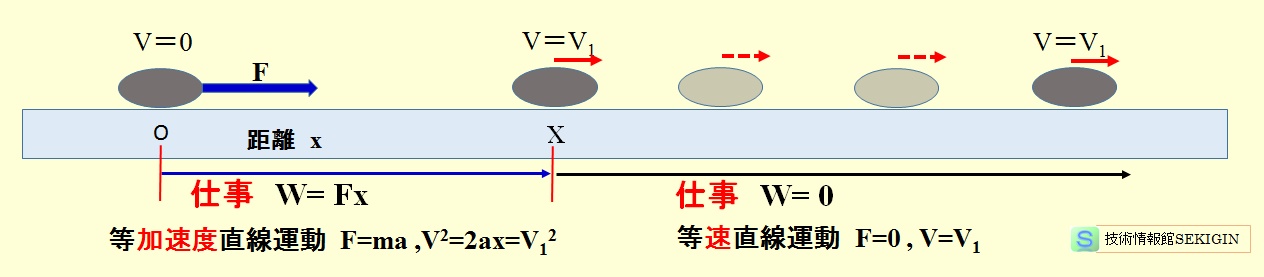
仕事とは
例に示した物体に働く力が一定で,直線的に移動する例は稀で,一般的な現象では,力や移動方向が変わることが多い。
これを考慮し,仕事を一般化すると,力を微少な量に区分し微少区間ごとに仕事を計算し,対象となる区間 a ~ b を合算(積分)しなければならない。
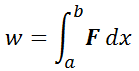
【参考:基礎用語】
- 等速直線運動(uniform linear motion , linear uniform motion)
等速度運動ともいわれ,物体が慣性の法則に従う運動のため,初速度の大きさと方向が維持される。 - ダイン( dyne ,記号 dyn )
CGS 単位系(cm ,g ,s )における力の単位で,1 ダインは,質量 1 グラム( g )の物体が力の方向に加速度 1 センチメートル毎秒毎秒( cm・s‐2 )を得た時の力。1 dyn = 1 g・cms‐2 なお,1993年11月施行の計量法で,力の単位にニュートン( N : newton )の使用が定められ,1995年10月以降の商取引でダインの使用が禁止された。 - エルグ( erg )
1 ダイン( dyn )の力がその方向に物体を 1 センチメートル( cm ) 動かすときのエネルギー。1 erg = 1 dyn・cm - ニュートン( newton ,記号 N )
質量 1 kg の質点に力を加えて,加速度 1 ms‐2 を得た時の力。1 N = 1 kg・ms‐2 - ジュール( joule ,記号 J )
1 ニュートン( N )の力がその力の方向に物体を1メートル( m )動かすときの仕事。1 J = 1 N・m - 流体の成す仕事
圧力 p ,移動した体積⊿V のとき,パスカルの原理とから w = p⊿V となる。単位は,Pa・m3=(N m‐2)・m3=Nm=J となる。 - ばねの変形で成す仕事
変形した長さ x のとき,フックの法則(ばね定数 の単位Nm‐1 )とから,w=kx2/ 2 となる。単位は,Nm‐1・m2=Nm=J - ジェームズ・プレスコット・ジュール(James Prescott Joule,1818 年~1889 年)
イギリスの物理学者。ジュールの法則の発見,熱の仕事当量,マイヤー,ヘルムホルツと共にエネルギー保存則(熱力学第一法則)の発見者,など熱力学の発展に寄与し,単位ジュール( J )として名をとどめる。 - ジュール( J )への単位換算
ニュートンメートル: 1 Nm = 1 J
エルグ: 1 erg = 10−7 J
重量キログラムメートル: 1 kgf・m = 9.80665 J
カロリー: 1 cal = 4.18605 J
ワット秒: 1 W・s = 1 J
クーロンボルト: 1 C・V = 1 J
電子ボルト: 1 eV ≒ 1.602×10‐19 J - 力のモーメント(moment of force)
力学において,物体に回転を生じさせるような力の性質を表す量で,力の能率とも呼ばれる。 - 主な固有の名称を持つ SI組立単位
ヘルツ (hertz) Hz = s‐1 :周波数
ニュートン (newton) N = m・kg・s‐2 :力
パスカル (pascal) Pa = N・m‐2 = m‐1・kg・s‐2 : 圧力・応力
ジュール (joule) J = N・m = m2・kg・s‐2 : エネルギー・仕事・熱量
ワット (watt) W = J・s‐1 = m2・kg・s‐3 :仕事率・工率・放射束
クーロン (coulomb) C = s·A :電荷・電気量
ボルト (volt) V = W・A‐1 = m2・kg・s‐3·A‐1 :電位差 (電圧)・起電力
ファラド (farad) F = C・V‐1 = m‐2・kg‐1・s4・A2 :電気容量
オーム (ohm) Ω = V・A‐1 = m2・kg・s‐3・A‐2 :電気抵抗
ウェーバ (weber) Wb = V・s = m2·kg・s‐2・A‐1 :磁束
テスラ (tesla) T = Wb・m‐2 = kg・s‐2・A‐1 :磁束密度 >
ページの先頭へ
【仕事の原理,仕事率】
地球表面上で,物体を同じ高さに持ち上げる場合の仕事を考える。持ち上げ方として,垂直に持ち上げる場合と斜面を使って持ち上げる場合に分ける。
垂直に持ち上げる時の仕事
重力加速度 g の地上で,質量 m の物体を高さ h だけ持ち上げる場合を考える。
持ち上げる力が物体に作用する重力( mg )と同じ場合は,力の釣り合いで静止(移動しない)するので,物体を持ち上げるためには,重力を超える任意の力( F )が必要である。
物体に加える力は任意であるが,高さ h で物体を止めるために仕事が必要で,重力を超える力で行った仕事と相殺され,最終的には重力と同じ力で持ち上げたと仮定できる。
従って,力が行った仕事は,
W = F h = mg h
となる。
斜めに持ち上げる時の仕事
重力加速度 g の地上で,質量 m の物体を仰角θの斜面に沿って,高さ h だけ持ち上げる場合を考える。
高さ方向に h だけ移動される場合の移動距離( l )は,三角関数を用いて,l = h/ sinθとなる。物体に加える力( F )は,重力(mg)の斜面の方向の成分(mg sinθ)と動摩擦力の和を超えなければ移動できない。
動摩擦力は,動摩擦係数μと斜面に対する垂直抗力とから,μmg cosθとなるので,物体を移動するための力は,F=mg sinθ+μmg cosθとなる。
従って,力が行った仕事は,
W = F l = (mg sinθ+μmg cosθ)・ h/ sinθ= mg h +μmg h・cotθ/ sin θ
となる。(なお,cotθ= 1/ tan θ= cos θ/ sin θ)
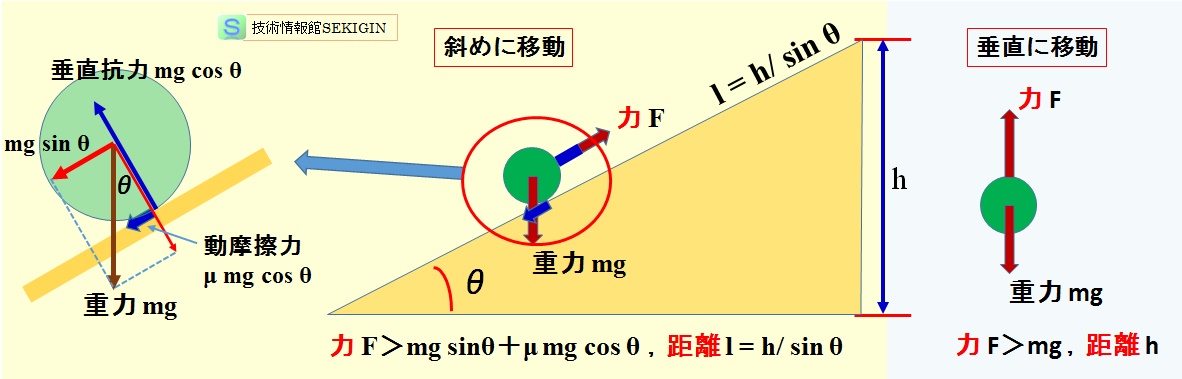
斜面での仕事
このように,摩擦力を考慮しない場合には,出発点と終点が同じ場合には,斜面を使う,滑車などの道具を持ちるなどで,必要とする力を低減しても,行う仕事は変わらない。これを仕事の原理という。
仕事率(power)
これまでの説明で明らかなように,仕事は,力と移動距離だけで決まり,早く移動しようがゆっくりと移動しようが同じ仕事である。
すなわち,日常生活で重要視される効率(能率)を評価対象とするには,仕事に要した時間( t )を考慮した評価が求められる。
このため,単位時間当たりの仕事,すなわち時間変化( ⊿t )で成された仕事( ⊿W )を割った仕事率( P )が定義される。
P = ⊿W/ ⊿t =F ⊿x/ ⊿t =Fν
仕事率は,力と速度でも表現できる。例えば,エンジンが一定の推進力で走行する自動車が,空気抵抗などとの釣り合いで,等速運動している場合に,エンジンの推進力と速度からエンジンの仕事率が求まる。
仕事率の単位は,国際単位系(SI)で,1 秒当たり 1 ジュール( J )の仕事率(ジュール毎秒(J/ s)を 1 ワット( W )と定義されている。
後述するように,仕事率と同等の概念に電力( Electric power )がある。電力( P )は電流( I )と電圧( V )の積 P = I × V で表され,単位にワット( W )が用いられる。
ページの先頭へ
【仕事の種類と単位】
力がする仕事
力(単位:kg・m・s‐2 =N)を受けた物体の変位(単位:m)の内積である仕事の単位は,ニュートンメートル(Nm=kg・m2・s‐2)となるが,この単位は,仕事とは概念の異なる力のモーメントの単位 Nm と混同する恐れが多い。
なお,古くは,力の単位には,ニュートン( N : newton )ではなく, CGS 単位系(1832 年提唱)のダイン( dyn := g・cm・s‐2 = 10‐5 N)が,仕事量にエルグ( erg:= g・cm2・s‐2 = 10−7 J )が用いられていた。
電気がする仕事
電力(electric power)を時間積分した電力量(electric(al) energy)と定義される。電力( P )は,単位時間に電流(I)がする仕事で電圧(V)との積 P = I × V で表され,単位をワット(W=V・V)と定義された。
従って,時間積分の電力量の単位は,ワット秒(Ws(=A・V・s))やワット時(Wh)で表される。
電力量は,電位差 1 V の 2 点間を 1 クーロン( C )の電気量が運ばれる電力量でもあり,単位は,クーロンボルト( C・V )で表される。なお,クーロン( C )とは,1 秒間に 1 アンペア( A )の電流で運ばれる電荷(電気量)で,単位は アンペア秒( A・s )で表される。
熱がする仕事
蒸気機関,ガソリン・ディーゼルエンジン,ガスタービン機関などの熱機関(heat engine)は,熱を仕事に変える装置である。高温物体から低温物体へ移動する熱,化学反応で発生,吸収される熱などの大きさは,熱量(quantity of heat)といい, 1 g 水の温度を 1 ℃だけ上げるのに必要な熱量を 1 カロリーと定義された。
仕事の単位
ジュールによるジュールの法則の発見や熱の仕事当量(mechanical equivalent of heat)に関する研究から,力学的仕事と電気的仕事,熱的仕事が交互に交換できることが示された。
● ジュールの法則(Joule's laws):導線に電流を通したとき,一定時間に発生する熱量( Q )は電気抵抗( R )および電流の強さ( I )の2乗に比例( Q= I2R=I・V )する。
● おもりによる重力で電磁石のコイルを回転させ,その結果発生する誘導電流の発熱を調べ,機械的力が消費される時にはいつでもそれに厳密に等しい量の熱が得られるとの結論を得た。
● 空気を水中で圧縮・膨張させ,そのときの水の温度変化を調べ,空気を膨張させたときは温度が下がることから仕事→熱の変化ではなく,熱→仕事という過程をはじめて測定した。
● 水中の羽根車をおもりの重力で回し,その運動で生まれる熱とおもりの重さと下がった長さから得られる仕事量を比較した。この実験は1845年から繰り返し行われ,1849年に行った実験で,現在の熱の仕事当量に近い値( J=4.15 J/cal )を得ている。
熱の仕事当量(mechanical equivalent of heat)
1 cal の熱量に相当する仕事の量で,一般に記号 J で表され,仕事 W と熱量 Q の間には
W = Q J
の関係にある。
単位は J/ cal で,現在の計量法附則第三条の計量単位等を定める政令 (平成四年十一月十八日政令第三百五十八号)では,J=4.18605(J/ cal)が用いられている。
仕事の単位は,分野により,ジュール( J ),ワット( W ),カロリー( cal )と異なったものが長い間用いられていたが,それぞれの仕事は相互に交換できる。
1948 年の第9回国際度量衡総会で,「1 ニュートン( N )の力がその力の方向に物体を1メートル( m )動かすときの仕事」を,英国の物理学者ジェームズ・プレスコット・ジュールに因んでジュール( J )と定義された。
また,同総会で,カロリーはできるだけ使用せず,もし使用する場合にはジュールを併記することと決議され,国際単位系(SI)ではカロリーは併用単位にもなっていない。
現在では,エネルギー,仕事,熱量,電力量の単位として,ジュールを用いるのが一般的となっている。
ページの先頭へ
【エネルギーとは】
「エネルギー」概念が創始されたのは,電気的仕事,力学的仕事,熱的仕事が相互に交換できることを示したジュールの時代(19世紀)である。
エネルギー(energy)は,“物体や系が持つ仕事をする能力”と定義される。すなわち,仕事とは,仕事の前後におけるエネルギー差と言い換えられる。
エネルギー保存則(law of conservation of energy)
物理的・化学的変化において,これに関与する各種のエネルギーの総和が,変化の前後で変らないという法則。
エネルギーの種類
エネルギーは,仕事をする能力と定義され,その瞬間に仕事をしていなくとも存在することになる。
力学的エネルギーは,運動エネルギーと位置エネルギーに分類される。熱力学では,仕事として取り出すことのできるエネルギーとして自由エネルギーが定義されている。自由エネルギーには,取り出す条件によってヘルムホルツエネルギーとギブズエネルギーの 2 つに分けられる。
力学的仕事と同等もしくは交換可能な仕事の能力(エネルギー)は,移動形態や保存形態による分類が多数ある。
力学的エネルギー(mechanical energy):機械的エネルギーとも呼ばれ,運動エネルギーと位置エネルギーの和。
運動エネルギー(kinetic energy):物体の運動に伴うエネルギーで,物体の速度を変化させる際に必要な仕事である。
位置エネルギー(potential energy):ポテンシャルエネルギーともいい,物体が「ある位置」にあることで物体が持つ(蓄えられた)エネルギー。位置エネルギーは,重力による質量あたりの重力ポテンシャル(gravitational potential),ばねやゴムなどの弾性体の変形に伴う弾性エネルギー(elastic energy),電荷の周りに発生する静電ポテンシャル(electrostatic potential)などがある。
自由エネルギー(free energy):化学エネルギーともいわれ,化学変化を含めた熱力学的系の系の最大仕事,自発的変化の方向(発エルゴン反応,吸エルゴン反応),平衡条件などを表す指標に用いられる。
厳密な定義はないが,慣習的に用いられるエネルギーの名称に次のものがある。
熱エネルギー(thermal energy):ある温度での物質の内部エネルギーから絶対零度における内部エネルギーを差し引いたもの。熱機関と熱浴との温度の差を利用して取り出されるエネルギー。
電気エネルギー(electrical energy):電流によって運ばれるエネルギー。
光エネルギー(light energy):電磁波の持つエネルギーや電磁波によって得られるエネルギー。
原子核エネルギー(nuclear energy):核エネルギー,原子力(atomic power),原子エネルギー(atomic energy)などともいい,原子核の変換や核反応に伴って放出される多量のエネルギー。
ページの先頭へ