物理 第三部：流体の物理

　流体動力学（fluid dynamics）は，18世紀に，ベルヌーイ，オイラー，ラグランジュによる完全流体（perfect fluid）の運動方程式，19世紀のナヴィエ，ストークスによる粘性流体（viscous fluid）の運動方程式により流体動力学の基礎が確立から発展した。
　
　その後のレイノルズによる乱流（turbulent flow）の概念，プラントルの境界層理論で現代の流体力学体系が整った。
　20世紀になると飛行機の発展による航空力学，高速流体力学が，宇宙ロケットの登場で極超音速流および希薄気体の力学，核融合炉での電磁流体力学などに発展している。
　
　発展に寄与した主な学者
　●　ダニエル・ベルヌーイ（1700年～1782年）
　スイスの数学者・物理学者。1738年に『流体力学』を出版。ベルヌーイの定理「空気や水の流れがはやくなると，そのはやくなった部分は圧力が低くなる。はやく流れるほど圧力は下がる。」など，流体力学の基礎を築いた。
　●　レオンハルト・オイラー（1707年～1783年）
　ロシア・ドイツの数学者・天文学者（天体物理学者）。オイラーの公式，オイラーの等式，オイラー積分など，微分積分の創始以来で，解析学の技法的な完成に寄与した。
　●　ジョゼフ＝ルイ・ラグランジュ（1736年～1813年）
　フランスの数学者，天文学者。オイラーと並ぶ18世紀最大の数学者。微分積分学の物理学，最小作用の原理に基づく解析力学（ラグランジュ力学）を作る。
　●　クロード・ルイ・マリー・アンリ・ナヴィエ（1785年～1836年）
　フランスの数学者，物理学者，流体力学の基礎方程式（ナビエ–ストークス方程式）。
　●　サー・ジョージ・ガブリエル・ストークス（1819年～1903年）
　アイルランドの数学者，物理学者， ストークスの式。
　●　オズボーン・レイノルズ（1842年～1912年）
　イギリスの物理学者，レイノルズ数，レイノルズの輸送定理。
　●　ルートヴィヒ・プラントル（1875年～1953年）
　ドイツの物理学者。空気力学における境界層，薄翼の理論，揚力線理論などで知られる。
　
　【参考：基礎用語】

• 完全流体（perfect fluid）
  　理想流体（ideal fluid），非粘性流体（inviscid fluid）ともいわれ，理想化して粘性を無視した取扱いをする仮想的な流体で，ベルヌーイの定理が成り立つ。
  　粘性が存在しないことは，流体が運動してもせん断応力（接線応力）が作用しないことと同義で，いわば力学での摩擦力の無視と同等に考えられる。
• 粘性流体（viscous fluid）
  　運動した際に接線応力が発生する流体。実用の流体は粘性を持つため，粘性流体に分類される。
• 乱流（turbulent flow）
  　流体の各部分の速度や圧力などが不規則に変動（乱れ）し，混合しながら流れる流れをいう。
  　乱れを含まない流れは層流（laminar flow）といわれる。レイノルズ数が低い場合には，流れは安定し層流状態を保つ。
• 境界層（boundary layer）
  　1904 年にドイツの物理学者ルートヴィヒ・プラントルが発見した物体表面に沿ってできる薄い層をいう。境界層は，レイノルズ数が非常に大きいとき，粘性流体の流れにおいて，物体表面に沿って，速度勾配（渦度）がきわめて大きい薄い層である。
• レイノルズ数（Reynolds number）
  　流体のとの比で定義される。粘性流体の流れにおける慣性力と粘性力の比を表わす。この概念はストークスが提唱（1851年）したが，イギリスの物理学者オズボーン・レイノルズ（Osborne Reynolds，1842年～ 1912年）の業績に因んでレイノルズ数と命名された。
  　レイノルズ数の小さい流れは，粘性の影響による減衰効果が大で，安定した流れである。一方，レイノルズ数が大きい流れは，一般に不安定で乱流になりやすい。
  　一般的に，一様な流れの中に円柱を固定した場合は，Re 1 を超えると渦が発生し始め，Re 40 を超えるとカルマン渦の発生，Re 1000 以上で乱れた状態（乱流状態）になるといわれている。
• 順圧（barotropic）
  　バルトロピックともいい，圧力が密度のみに依存（等圧面と等密度面が一致）することをいう。この性質の流体をバルトろぴー流体という。

　流体の未知変数について
　流体の運動を表現するためには，次の 5 つ変数が必要となる。
　速度：位置 ( x , y , z ) で，時間 t の速度（ 3 変数）
　　　　　X 軸方向の速度 μ (x , y , z , t )
　　　　　Y 軸方向の速度 ν ( x , y , z , t )
　　　　　Z 軸方向の速度 ω ( x , y , z , t )
　密度：流体の質量は，形が定まっていないので，単位体積あたりの質量として，
　　　　　密度 ρ ( x , y , z , t )
　圧力：p ( x , y , z ,t )
　
　多くの流体では，密度が一定（ρ= 一定）であったり圧力が密度に依存（ p(ρ) ）したりする。圧力が密度に依存することを順圧（barotropic）やバルトロピックといい，この性質の流体をバルトロピー流体という。
　従って，バルトロピー流体では，最終的な未知変数は速度（μ，ν，ω）と圧力 p の 4 つになる。

　流体の運動の記述法には，オイラー的記述法（Eulerian specification）とラグランジュ的記述法（Lagrangian specification）がある。
　オイラー的記述法は流体の流れの理解に便利で，ラグランジュ的記述法は運動方程式をたてる際に便利である。
　なお，両者の時間微分の意味が異なるが，後述のように，両記述法を結びつける関係式が存在する。
　
　オイラー的記述法
　オイラー的記述法とは，流体を第三者の立場にたって観察する方法，すなわち座標軸と相対的に固定された点で物理量の変化を見た記述である。
　
　オイラー的記述では，空間座標　𝒓 = ( x , y , z ) と時間 t が独立変数（independent variable）で，速度，密度，圧力が従属変数（dependent variable）となる。
　すなわち，位置 ( x , y , z ) で，時間 t の X 軸方向の速度 μ( x , y , z , t ) ，Y 軸方向の速度 ν( x , y , z , t ) ，Z 軸方向の速度 ω( x , y , z , t ) ，密度 ρ ( x , y , z , t ) ，圧力 p ( x , y , z ,t ) が従属変数である。
　
　ラグランジュ的記述法
　ラグランジュ的記述法とは，流体を構成する流体粒子が時間的にどのように動くかに注目し，粒子の初期位置と時間の関数として記述する方法である。
　従って，各流体粒子の初期時刻 t = 0 での位置ベクトル 𝒓₀ ( x₀ , y₀ , z₀ ) を目印として，この流体粒子の時刻 t での位置ベクトル 𝒓 ( x , y , z ) とした時，𝒓 = 𝒓 (𝒓₀ , t ) で表される。
　
　ラグランジュ的記述において，流体粒子の初期位置 𝒓₀ と時間 t が独立変数で，粒子の位置ベクトル 𝒓 (𝒓₀ , t ) ，速度 U (𝒓₀ , t ) などが従属変数となる．
　例えば，流体粒子の位置ベクトル r の時間変化率（偏微分）を求めれば，その粒子の速度 U を求めたことになる。
　　　　　　　U ＝ U (𝒓₀ , t ) ＝ 𝜕𝒓 / 𝜕t

　オイラー的記述において，流体粒子の物理量が時間的にどのように変化するのかを調べたいとき，流体粒子の流れに注目した時間的変化を表す時間微分を物質微分（material derivative），ラグランジュ微分（Lagrangian derivative）や実質微分と呼び D/ Dt と表記される。なお，座標軸に相対的に固定された点における局所的な時間変化の偏微分 𝜕/ 𝜕t は，オイラー微分（Eulerian derivative）と呼ばれる。
　
　速度，密度，圧力などの物理量（physical quantity）を 𝑓 とすると，オイラー的記述では，空間座標 𝒓 ( x , y , z ) と時間 t の関数 𝑓 ( x , y , z , t ) となる。
　ここで，注目する流体粒子がdt 時間後に 位置 ( x+dx , y+dy , z+dz ) に微小量移動した時の物理量は，関数 𝑓 ( x+dx , y+dy , z+dz , t+dt ) となる。
　この時の物理量の増加分 d𝑓 は，
　　　　　　　d𝑓 ＝ 𝑓 ( x+dx , y+dy , z+dz , t+dt ) － f ( x , y , z , t )
となる。ここで，𝑓 ( x+dx , y+dy , z+dz , t+dt ) は，一次近似により
　　　　　　　
とできるので，物理量の増加分は，
　　　　　　　
となる。
　
　ここで，移動した距離は，移動速度に時間を掛けて得られるので，X 軸方向の速度 μ( x , y , z , t ) ，Y 軸方向の速度 ν( x , y , z , t ) ，Z 軸方向の速度 ω( x , y , z , t ) とすると，
　　　　　　　dx =μ( x , y , z , t ) dt ，dy =ν( x , y , z , t ) dt ，dz =ω( x , y , z , t ) dt
とできる。
　
　従って，特定の流体粒子に注目したときの関数 f の時間変化の割合（物質微分）は，
　　　　　　　
となる。
　物質微分は流体力学における運動方程式を導く際に使用される。

　関数 𝑓 (x ) のx = a 近傍での近似値は，関数 𝑓 (x ) を x = a でテイラー展開（Taylor expansion）することで，
　　　　　　　
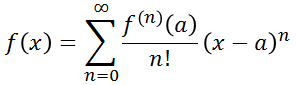
とできる。なお，n! は n の階乗，𝑓⁽ⁿ⁾ (a) は， x = a における ƒ の n 次微分係数である。また，(x − a)⁰ は便宜的に 1 と定義される。
　
　ここで，（ x‐a ）の値が十分に小さい場合は，高次の項を無視できる。n 次の項まで考えたものを n 次近似という。すなわち，3 次以上を無視した場合を 2 次近似，2 次以上を無視した場合を 1 次近似という。
　上式の 1 次近似は，
　　　　　　　
で表される。