物理 第四部：波・波動の物理

　流体力学における重力波（gravity wave）とは，水面波ともいわれる表面波（surface wave）の一種で，海や湖などで身近に見られる波である。
　
　液体や気体などの流体は，圧縮に対する弾性（elasticity）はあるが，ずれに対する弾性はない。このため，流体では，横波は現れず，縦波のみが起きる。
　一方，液体の界面における波動（重力波）は，一見すると媒質の上下運動で進む横波のように見られるが，波動の基礎で紹介したように，重力や表面張力（surface tension）を復元力とする波で，横波とは区別される。
　すなわち，重力場において，力学的平衡状態の媒質（水など）が，変位した場合に，重力を復元力として元の状態に戻る過程で界面に沿って進む波長の長い波動である。
　池などで観察されるさざ波は，水の表面張力が復元力となって起こる波長 1.7 cm 以下の短い表面張力波（capillary wave）で，重力波とは発生原理が異なる。
　
　なお，同じ日本語表記の重力波（gravitational wave）は，一般相対性理論における変動する重力場が光と同じ速さで波として伝わる現象で，流体力学の重力波（gravity wave）とは異なる定義のものである。
　
　海上で重力を復元力とする重力波（波）には，発生原因により次の区分がある。
　風によって起きる波を波浪（ocean waves）といい，風の影響で直接発生した波浪を風浪（wind sea）や風波（かざなみ，ふうは）という。
　他の海域で発生した波浪が伝わってきた波をうねり（swell）という。波浪の周期は 1～30 秒程度で，風浪とうねりからなる。発達した風浪ほど波高が大きく，波長や周期が長い。うねりは，波長 100m 以上，周期 8 秒以上のものが多い。
　海水が風で吹き寄せられて海面が上昇する現象，台風や発達した低気圧の影響で気圧が下がり，海面が吸い上げられ上昇する現象などは，高潮（storm surge）といわれる。高潮は波長が長いので風津波ともいわれる。
　
　風以外の原因の波では，船舶の航行時に後ろに発生する波を引き波（dilatational wave , back wash）といい，地震によってできる波を津波（tsunami），海水の潮汐現象で生じる波を潮汐波（tidal wave）という。
　
　海上の重力波，特に波浪は，その場所で吹いている風によって生じた波のため，個々の波は不規則で尖っている。不規則な波の高さを表現するため，波の振幅とは別に，次のように定義される用語が用いられる。
　波動論の振幅の二倍に相当する波の山から谷までの高さを波高（wave height）といい，ある地点で一定時間（気象庁では 20 分間）に観測される波のうち，高いほうから順に 1/3 の個数までの波を有義波（significant wave）といい，これを平均した波高を有義波高（significant wave height）という。
　なお，有義波の中で最大のものを最大波高といい，有義波高が 4 m を超える場合をしけ（時化）という。
　
　海の波について
　波の中でも海の波は，最も身近なものの一つである。海の波は，海岸近くの波と沖合の波で物理的な取扱いが異なる。
　沖合の波のように，水面変動の振幅に比較して，水深が十分に大きい場合の波を微小振幅波（small amplitude wave），沖波（offing wave），深海波（deep water wave，深水波）などといい，これを扱う理論を微小振幅波理論（small amplitude waves theory）という。
　一方，海岸付近など，水深に比較して波高がそれほど小さくない場合は，有限振幅波（finite amplitude wave），浅海波（せんかいは，shallow water wave，浅水波），長波（long wave）などといい，これを扱う理論を有限振幅波理論（finite amplitude waves theory）という。
　
　【参考：基礎用語】

• 弾性（elasticity）
  　力を加えて変形（ひずみ）した物質が，力の除去で元の形に戻ろうとする性質。
• 表面張力（surface tension）
  　液体の表面に作用する表面積をできるだけ小さくしようとする力。液体表面の単位面積当たりの自由エネルギーで表す。（ JIS K 3211「界面活性剤用語」）
  　一般に，二相間の界面において，界面の面積を縮小するように働く界面張力という。表面という場合は，気・液界面，気・固界面をいうので，この界面の界面張力を特に表面張力という。
• 界面張力（interfacial tension）
  　単位面積当たりの界面自由エネルギー。
• 界面自由エネルギー（surface free energy）
  　液体や固体の界面が内部に比べ過剰にもっている自由エネルギー。

　水面変動の振幅に比較して，水深が十分に大きい場合の波を扱う理論で，理論が成立するため前提を次に示す。
　
　自由表面波（free surface wave）
　水深一定の水平な底の上にある水の表面の波をいう，自由表面波は，水の粘性が無視できるほど小さいので，非圧縮性完全流体として扱える。
　自由表面波に作用する外力が保存力である重力のみの場合は，ラグランジュの渦定理により，非圧縮性渦なし完全流体の流れ（ポテンシャル流）としての取り扱いが可能になる。
　
　保存力（conservative force）
　位置 r での位置エネルギー（ポテンシャル）を U(r) とすると，保存力は F ＝‐grad U(r) ＝‐∇ U(r) で与えられる。なお，grad はスカラー場のベクトル微分（勾配），∇はナブラである。
　
　ラグランジュの渦定理（Lagrange's vortex theorem）
　ラグランジュの渦定理とは，
　① 流体のある部分が初期に渦なし運動をしているとき，その実質部分は渦なし運動を持続する。
　② ある時刻に渦度が 0 でないとき，その実質部分は以後も 0 でない渦度をもつ。
の 2 か条を指す。
　この2か条をまとめると「渦は新たに発生することも，また消滅することもない」といえる。
　なお，渦度（vorticity，うずど，かどと読む）とは，流体が自転している部分を渦といい，渦の強さ（ベクトル量）をいう。
　
　連続の方程式（equation of continuity）
　流体の運動で紹介したように，定常流の中に一つの流管を考えた時，その中の任意の点における速さν，流管の断面積 S ，流体の密度ρとした時，単位時間にその点を通過する流体の質量が変わらないので，
　ρνS ＝一定
の関係が得られる。これを連続の方程式という。
　なお，流体が液体のように，圧力が変わっても密度変化の非常に小さい非圧縮性流体（incompressible fluid）では，
　νS ＝一定
と書ける。
　
　【参考：基礎用語】

• 完全流体（perfect fluid）
  　理想流体（ideal fluid），非粘性流体（inviscid fluid）ともいわれ，理想化して粘性を無視した取扱いをする仮想的な流体で，ベルヌーイの定理が成り立つ。
  　粘性が存在しないことは，流体が運動してもせん断応力（接線応力）が作用しないことと同義で，いわば力学での摩擦力の無視と同等に考えられる。
• 連続の方程式（equation of continuity）
  　連続方程式，連続の式，連続式などといい，「突然現れたり消えたりすることはない」という考え方を表す。一般には，流体力学における質量保存の法則を表わす偏微分方程式をいう。
• 非圧縮性流体（incompressible fluid）
  　一般に圧力によって流体の密度が変化するので圧縮性流体（compressible fluid）と呼ばれるが，流体の速度（圧力変化）が小さく，密度の変化が無視できる場合には非圧縮性流体として扱われる。

　ここで，水深 h ，水面上の波の進行方向を x 軸，それと垂直な方向に y 軸をとり，鉛直上方に z 軸をとる。
　微小振幅波理論が成立するため仮の仮定は，非圧縮性完全流体であること，重力のみが外力として作用すること，水面の圧力をゼロ（大気圧に等しい）とすること，水深一定で，水底が水に対し不透過であること，三角関数（sin , cos）で表される保存波（定型波）であること，渦なし流れで速度ポテンシャルが使え，一方向に進む鉛直2次元的な波である。
　
　基本方程式について
　水平方向の流速を u = u(x,z,t) ，垂直方向の流速を w = w(x,z,t) とすると，連続の方程式から流速の偏微分は，
　　　　　　　
となる。
　速度 v(u,w) は速度ポテンシャル（velocity potential）ψで表すと，
　　　　　　　
とできるので，連続の方程式とから
　　　　　　　
となる。これは速度ポテンシャルの基礎方程式（ラプラスの方程式）となる。
　
　速度ポテンシャル（velocity potential）
　流体力学で，渦なし流れの解析に用いられる。渦なし流においては，速度ベクトルを u ，渦度ベクトルを ω とすると，ω＝rot u＝0 であるから，関数の値がスカラー値を取る適当なスカラー関数ψを用いて，u＝gradψと書ける。このψを速度ポテンシャルという。
　特に非圧縮性流体においては，連続の方程式 div u＝0 から，△ψ＝0 ( △ はラプラシアン ) となる。すなわち，速度ポテンシャル ψ は調和関数であり，境界条件を満たす調和関数ψが決れば，流れの速度場 u はただちに決定される。
　
　境界条件について
　水底
　不透過の水底を前提としているので，境界条件として，底を突き抜ける水（下向き）の速度がゼロ，すなわち水底（ z＝‐h ）での鉛直方向流速 w が，
　　　　　　　
　水面
　水面の水粒子が飛び出さない（水面の水分子がいつまでも水面にある）とすると，水面の変位が z = η (x,t) のとき，水面近く（ z＝η ≈ 0 ）での鉛直方向流速 w は，
　　　　　　　
と，水面の上昇速度（ ∂η/ ∂ t ）は，水面の水粒子の鉛直方向流速に等しいと置ける。
　
　次いで，圧力 P は非定常流のベルヌーイの式で与えられるので，重力場で水の密度ρ重力加速度 g とすると，
　　　　　　　
で与えられるので，水面近く（ z＝η ≈ 0 ）での圧力をゼロ（大気圧に等しい）とすると，
　　　　　　　
とできる。
　従って，
　　　　　　　
からη を消去すると，
　　　　　　　
が得られる。
　水面の波形
　水面の波形は x 軸方向に進行する三角関数（sin , cos）で表される保存波（定型波）と仮定されているので，振幅を a ，波数を k ，振動数（各周波数）をωとすると，
　　　　　　　η (x,t) = a sin(kx − ωt)
で表される。

　微小振幅波理論の解析より
　前出の基本方程式を適切な仮定と境界条件のもとで解くことができる。重力加速度 g ，水深 h ，波高 H ，振動数（角周波数）ω（= 2π/ T；T は周期），波数 k（= 2π/ λ；λ は波長）としたときの速度ポテンシャルφを求めると，
　　　　　　　
となる。なお，cosh は双曲線余弦関数である。
　この式から，水粒子が楕円軌道を描いて運動することが分かる。式の導出は省略するが，水深と水粒子の運動との関係は次の通りである。
　水深 h が大きい水面波（深海波）では，kh（＝2πh/ λ＞π）が著しく大きく，水平方向と鉛直方向の流速の最大値が一致するので，波を構成する水粒子は円運動になる。
　水深 h が小さい水面波（極浅海波）では，kh（＝2πh/ λ＜π/ 10 ）が著しく小さく，水平方向の流速が水深方向に一定で，海底付近でも大きく動く。
　また，鉛直方向の流速が水深方向に線形で減少するので，波を構成する水粒子の軌跡はかなり鉛直方向に潰れた楕円を描き，水底付近の水粒子は水平方向にだけ動く。
　振動数と波数の関係（分散関係式）は，
　　　　　　　
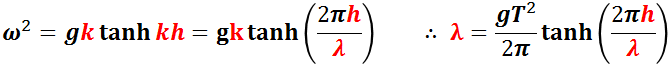
で与えられる。なお，tanh は双曲線正接関数である。
　この式から，波長と周期と水深には一定の関係があり，波長と周期を勝手に決めることはできないことが分かる。．
　
　重力波の位相速度について
　位相速度（phase velocity）とは，波の山や谷の特定の位置が移動する速度のことで，伝播速度ともいわれる。
　波の位相速度 V は，分散関係式，波の波長λ，鉛直方向の高さ（深さ）h を用いて，
　　　　　　　
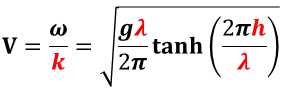
と得られる。すなわち，波の位相速度は，波長に依存することが分かる。
　双曲線正接関数 tanh A は，単調増加関数であり，A →∞でtanh A ≒ 1 と近似でき，A ≪1 では tanh A ≒ A と近似できる。
　従って，水深が波の波長より著しく大きい場合の位相速度は，
　　　　　　　
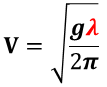
となり，位相速度が波長λに依存し，水深 h に依存しないことが分かる。
　一方，遠浅の海岸など，水深が波長より短い場合は，
　　　　　　　
と，位相速度は波長λに依存せず，水深 h に依存することが分かる。

• ラプラスの方程式（Laplace equation）
  　三次元のスカラー関数が満足する二階偏微分方程式
• 分散関係（dispersion relation）
  　角周波数（角振動数）と波数の間の関係を分散関係といい，特に角周波数 ω を波数 k の関数で表した式を分散関係式という。
• 双曲線関数（hyperbolic function）
  　三角関数と類似の関数で，標準形の双曲線を表示するときに用いられる。
  　双曲線正弦関数（hyperbolic sine：sinh x ）
  　双曲線余弦関数（hyperbolic cosine：cosh x ）
  　双曲線正接関数（hyperbolic tangent：tanh x ）
  などがある。一般に，双曲線関数は，指数関数を用いて定義される。
  　　　
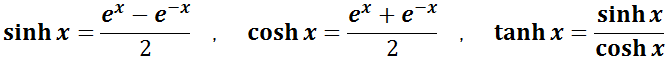
  　x が十分に大きい場合は，双曲線関数 sinh x ≈ e^x ，cosh x ≈ e^x ，tanh x ≈ 1 で近似される。
  　x が十分に小さい場合は，双曲線関数 sinh x ≈ x ，cosh x ≈ 1 ，tanh x ≈ x で近似される。