物理 第四部：波・波動の物理

　音波（acoustic wave）とは，一般的には，空中を伝播する人間や動物の可聴周波数（約16〜20000Hz）の弾性波を指すことが多いが，物理的には，気体，液体，固体を問わず，物体（弾性体）を伝播するすべての弾性波を指す。
　
　波動の基礎で紹介したように，液体や気体の内部では，ずれに対する弾性が無く，圧縮に対する弾性のみであるため，横波は現れず縦波である疎密波のみが起きる。固体の内部では，縦波のほかに横波であるせん断波（ねじれ波）も生じる。
　
　空気中を伝わる音など体積弾性率 K ，密度 ρの気体中を速さ c で伝わる縦波の波動方程式は，
　　　　　　　
で与えられる。
　
　【参考：基礎用語】

• 弾性波（elastic wave）
  　音波や地震波などの弾性体内を伝わる波をいう。 弾性体が固体の場合は，変位方向により，体積変化に伴う体積弾性による縦波，体積変化がなく形状変化に伴う形状弾性による横波に分けられる。
  　弾性体が流体の場合は，密度変化（体積変化）に伴う縦波だけで，横波はない。
• 疎密波（compression wave）
  　圧縮波ともいい，縦波の 1 種で，音波や地震の P 波など流体や弾性体に加わった圧力で局所的な密度変化が生じた波である。
• ねじれ波（shear wave）
  　横波，たわみ波，剪断波などとも呼ばれ，地震の S 波など弾性体の伝播方向と垂直な方向に振動（ねじれの状態を伝える）する波をいう。
• 弾性率（elastic modulus）
  　弾性定数，弾性係数ともいい，弾性体の応力とひずみの比をいう。
  　比例限度内では応力とひずみは比例（フックの法則）するので弾性率は物質により決まる定数となる。応力とひずみの種類により，ヤング率，剛性率，体積弾性率，ポアソン比等がある。
• ヤング率（Young's modulus）
  　縦弾性係数（modulus of longitudinal elasticity）ともいい，弾性限界内での固体の一方向（同軸方向）のひずみと応力の比例係数（弾性率）をいう。⇒　弾性率
• 剛性率（shear modulus）
  　ずり弾性率，せん断弾性係数ともいい，固体のずれ変形を起こさせる応力（せん断応力）とひずみ（角度で表される)との比をいう。弾性限界内では定数（弾性率）となる。⇒　弾性率
• 体積弾性率（bulk modules）
  　流体などの圧力と体積ひずみの比をいう。弾性限界内では定数（弾性率）となる。⇒　弾性率
• ポアソン比（Poisson's ratio）
  　物体に弾性限界内で応力を加えたとき，応力に直角方向に発生するひずみと応力方向に沿って発生するひずみの比のをいう。⇒　弾性率
• フックの法則（Hooke's law）
  　弾性の法則とも呼ばれ，物理学における主要な法則の一種，17世紀にイギリスの物理学者ロバート・フックが“ばねの伸びと弾性限度以下の荷重は正比例する”と提唱した近似的な法則である。
  　フックの法則が近似として成り立つ物質を線形弾性体，フック弾性体 (Hookean elastic material) という。

　波動方程式の導出は次の通りである。
　下図の左に示すように，気体中に断面 P ，Q で囲われた微小部分を考える。
　まず，距離 dx と僅かな距離の断面 P ，Q が，ある時刻に断面 P’ ，Q’に移動した時，断面 P の変位（ P-P’ ）を位置 x と時間 t の関数 (y)_x で表したとき，与えられた時刻では，x の関数となるので，断面 P と Q の変位の勾配は，
　　　　　　　
とでき，断面 P の変位量 P-P’ を(y)_x = y とすると，断面 Q の変位量 Q-Q’ は，
　　　　　　　
となる。
　これにより，断面 P ，Q の変位量の差の割合，すなわちひずみεは，
　　　　　　　
で与えられる。
　従って，断面 P’ に作用する応力σは，フックの法則により，弾性率 K とひずみεの積で与えられる。
　一方，応力は位置と時間の関数なので，σ＝f (x ,t) とおいて，
　　　　　　　
となる。
　断面 P ，Q の距離を限りなく小さくできるので，ここで示した応力の式は，任意の断面に適用できる。
　
　そこで，下図の右に示すように，改めて距離 Δx 離れた位置に断面積 S の断面 P ，Q を考える。
　応力の作用していない状態で，気体の密度をρとすると，断面 P ，Q 間の質量はρS Δx で与えられる。
　次いで，ある時刻 t で断面 P ，Q が断面 P’ ，Q’ に移動したとする。これにより断面 P’ に応力 f (x ,t) が，断面 Q’ に応力 f (x+Δx ,t) が現れるので，応力の勾配
　　　　　　　
から断面 P’ と断面 Q’ との応力差は
　　　　　　　
となる。
　
　ここで，断面 P’ ，Q’に移る運動方程式（ ma = F ）は，断面で囲われた領域の質量（ρS Δx ）に変化がないので
　　　　　　　
　
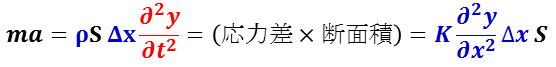
　これにより，波動方程式
　　　　　　　
が得られる。

　音速（speed of sound）とは，物質（媒質）中を伝わる音波の速度をいう。物質自体の振動で伝わるので，物質の特性で決まる 1 種類の物性値（弾性波伝播速度）となる。 代表的な物質での音速を次に示す。
　
　気体中の音速
　気体の定圧比熱容量と定積比熱容量の比である比熱比 γ，気体定数 R ，気体温度 T ，気体の平均分子量 M ，気圧 P ，気体の密度ρとした時の乾燥気体中の音速 c は，
　　　　　　　c²＝γRT/ M　，又は　c²＝γP/ ρ
で与えられる。
　例（ 1 気圧 0℃）：乾燥空気（331.45 m/s），水蒸気（473 m/s），ヘリウム（970 m/s），水素（1269.5 m/s）
　流体の流れの速さの単位として用いられるマッハ数（Mach number）は，流体の相対速度と音速の比で求まる無次元量である。この場合の音速には，便宜上で約 340 m/s（国際標準大気，気温 15℃，1,013 hPa）を用いているが，音速は大気の温度，平均分子量（気圧），比熱比，相対湿度などに影響されるため，マッハ数では的確な速度の評価には向かない。
　
　液体中の音速
　液体の圧力に対して体積がどの程度変化するかを表す圧縮率（compressibility）の逆数の体積弾性率 K ，液体の密度ρとした時の液体中の音速 c は，
　　　　　　　c²＝ K/ ρ
で与えられる。
　例（常温）：海水（1513 m/s），淡水（1500 m/s），水銀（1450 m/s），ベンゼン（1295 m/s），エタノール（1207 m/s），
　
　固体中の音速
　気体と液体は，縦波（弾性波）のみであるが，固体では縦波の他に横波も発生する。
　固体の剛性率 G ，体積弾性率 K ，密度ρとした時の縦波の音速 c は，
　　　　　　　c²＝ ( K+ 4G/ 3 )/ ρ
で与えられ，横波の音速 c は，
　　　　　　　c²＝ G/ ρ
で与えられる。
　式から分かるように，縦波は横波より早く，物質によっては倍以上の場合もある。
　例（常温，縦波；横波）：ベリリウム（12890 m/s ；8880 m/s），アルミニウム（6430 m/s ；3040 m/s），鉄（3240 m/s ；1220 m/s），氷（3230 m/s ；1600 m/s），ポリエチレン（1950 m/s ；540 m/s），天然ゴム（1500 m/s ；120 m/s）
　
　【参考：基礎用語】

• 比熱容量（specific heat capacity）
  　単に比熱とも呼ばれ，単位は J･kg^‐1･K^‐1 である。なお，一般的には，温度によって変化するので，比熱容量を表示する場合は，温度の指定が必要である。
  　原子量，分子量（モル）当たりの熱容量を原子熱（比熱容量×原子量），分子熱（比熱容量×分子量）という。分子熱は，モル比熱，モル熱容量とも呼ばれる。
  　液体や固体の体積は，温度による極端な変化はないが，気体は，温度によるエンタルピーや体積の変化が大きいため，圧力を一定に保ちながら測定した値と体積を一定に保ちながら測定した値で大きな違いがでる。
  　前者を定圧比熱容量（specific heat capacity at constant pressure），後者を定積比熱容量（specific heat capacity at constant volume）や定容比熱容量といわれている。
• 比熱比（specific heat ratio , heat capacity ratio）
  　1 モル当たりの定圧比熱容量（ C_p ）と定積比熱容量（ C_V ）との比（ C_p/ C_V ）をいい，通常は記号γ（又はκ）を用いて表す。
• 気体定数（gas constance）
  　ボイル・シャルルの法則 PV / T ＝ C（一定）の定数を気体定数とよび，記号 R で表記される。
  　0 ℃ 1 気圧（ 101325 Pa）の気体 1 mol の体積（モル体積）は，約 22.414 L なので，ボイル・シャルルの法則から， C ≒ 8.3145 Pa・m³・mol^{– 1}・K^{– 1} と計算される。
  　なお，気体定数の単位は， エネルギーの単位 J（ N・m ）を用いた J・K^{– 1}・mol^{– 1} が一般的に用いられる。
  　2010年 CODATA の推奨する気体定数は，R = 8.3144621(75) J・K^{– 1}・mol^{– 1} である。
• 圧縮率（compressibility）
  　液体の圧力に対して体積がどの程度変化するかを表す。なお，圧縮率は，体積弾性率の逆数である。

　音色（tinbre）
　ねいろの他におんしょくとも読まれる。音色は，人間が音を区別して感ずることができるための音の属性の一つで，音の大きさ，音の高さと音色とを音の三要素という。
　JIS Z 8106「音響用語」では，“聴覚に関する音の属性の一つで，物理的に異なる二つの音が，たとえ同じ音の大きさ及び高さであっても異なった感じに聞こえるとき，その相違に対応する属性。備考：音色は，主として音の波形に依存するが，音圧，音の時間変化にも関係する。”と定義している。
　音響学的では，音を周波数成分に分解（音のスペクトル）し，周波数成分のうち最も周波数の低いものを基音，それ以外を上音とし，上音の構成から音色の違いを識別している。
　
　音の高さ（pitch）
　ピッチともいい，JIS Z 8106「音響用語」では，“聴覚にかかわる音の属性の一つで，低から高に至る尺度上に配列される。備考： 複合音の音の高さは，主として刺激の周波数成分に依存するが，音圧，波形にも関係する。音の高さは，人がその音と同じ高さであると判断した純音の周波数で表すことがある。”と定義されている。
　音の高さの単位は，メル（mel）である。正面から提示された，周波数 1 000Hz ，音圧レベル 40dB の純音の高さを 1000 メルとする。備考：被験者が 1 000 メルの n 倍の高さと判断する音の高さが n×1000 メルである。
　
　音の強さ（sound intensity）
　音響パワー密度，音響エネルギー束密度，音響インテンシティともいわれ，JIS Z 8106「音響用語」では，“指定された方向に垂直な面を通過する音響エネルギー束をその面積で除した値。”と定義されている。
　音響エネルギー束（sound energy flux）とは，対象とする面を通過する瞬時音圧と体積速度の同相成分の積の時間平均値である。
　音の強さの単位
　ある指定された方向の音の強さの基準の音の強さに対する比の対数を音の強さのレベルという。比の 10 を底とする対数（常用対数）を採り，10倍すれば，音の強さのレベルはデシベルで表される。
　備考： 単位記号は，dB。特に指定がない限り，基準の音の強さは，1pW/m²。
　
　音の大きさ（loudness）
　ラウドネスともいわれ，JIS Z 8106「音響用語」では，“聴覚に関する音の属性の一つで，小から大に至る尺度上に配列される。備考：音の大きさは，主として刺激の音圧に依存するが，周波数，波形及び継続時間にも依存する。”と定義されている。
　音の大きさの単位
　音の大きさのレベル（loudness level）は，ある音について，正常な聴力をもつ人がその音と同じ大きさであると判断した自由進行波の 1 000Hz の純音の音圧レベルに等しい値。指定された回数の判断を行い，その中央値を採る。単位は，フォン。
　
　【参考：基礎用語】

• 音圧（sound pressure）
  　ある時間内の瞬時音圧の実効値をいい，瞬時音圧（instantaneous sound pressure）とは，媒質中のある点で，対象とする瞬間に存在する圧力から静圧を引いた値である。
• 音圧レベル（sound pressure level）
  　ある音圧の基準の音圧に対する比の対数をいい，比の 10 を底とする対数（常用対数）を採り，20 倍すれば，音圧レベルはデシベル（dB）で表される。
  備考： 特に指定がない限り，基準の音圧は，空中伝搬音に対しては 20µPa ，空気以外の媒質に対しては 1Pa。また，特に指定がない限り，音圧は実効値で表されているものとする。
• デシベル（decibel）
  　ベルの 1/10 の値。ベル（bel）とは，対数の底を 10 としたときの，パワーに比例する量のレベルの単位。また，対数の底を 10 の平方根［10 を底とする対数（常用対数）の値の 2 倍］としたときの場の量のレベルの単位。
• レベル（level）
  　ある量とその量の基準の量との比の対数。対数の底，基準の量及びレベルの種類を明記する必要がある。
  備考：レベルの種類は，着目した量を表す用語と組み合わせて示す。例えば，音圧レベル，音響パワーレベルなど。

　ドップラー効果（Doppler effect）とは，光や音などの波を発生している波源（音の場合は発音体）やそれの観測者の運動によって，波の振動数が変化して観測される現象をいう。
　ドップラー効果は，オーストリアの物理学者クリスティアン・ヨハン・ドップラーが，1842 年に，二重星の観測で光の色が変化するのを発見したのが最初といわれている。
　音のドップラー効果は，オランダの化学者クリストフ・ボイス・バロットが，列車に乗ったトランペット奏者の出す音を絶対音感を持った音楽家が観察し，音程の変化を1845 年に証明した。
　発音体 S（Source）の周波数 f と観測者 O（Observer）聞くstrong>周波数 f’の関係は，S の動く速度 v_S ，O の動く速度 v_O ，音の速度 c で決まる。
　　　　　　　
　速度 v_S と 速度 v_O は，S とOの移動方向や相対的位置により正負，の記号を変えることで対応できる。
　発音体から観察者に向かう向きを正としたとき，発音体が観察者から遠ざかるときは速度 v_S を負に（f’< f ），観察者が発音体に近づくときは速度 v_O を負に（ f’> f ）することで適用できる。
　
　光のドップラー効果
　音のドップラー効果と異なり，発振源（光源）や観察者が運動しても光の速度 C が変わらない（特殊相対性理論）ので，光源が観測者から見て角度θ の方向に速さ V で運動している場合の観察者に届く光の振動数ν’は，
　　　　　　　
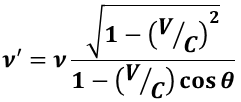
で与えられる。

　音波が空気中をある方向に伝わる時，空気のある部分が次の部分に力を及ぼして仕事をする。すなわち，エネルギーが音波の進む方向に伝わる。
　波は，1 周期の間に，1 波長進む。従って，1 波長に含まれるエネルギーを計算することで，単位時間について平均のエネルギーの流れを知ることができる。
　エネルギーは，空気の各部分の変位のための運動エネルギーと平均の密度から圧縮，又は膨張させられるための位置エネルギーで構成される。
　
　運動エネルギー
　振動数 f （波長λ），振幅 a の音波が x 軸に沿って進む時，ある部分が時刻 t に変位 y を生じたとすると，変位 y は，
　　　　　　　
となる。従って変位の速度 v は，
　　　　　　　
で与えられる。
　波動の無いときの気体の密度ρとし，音波の進行方向に垂直な単位断面積の部分を考えると，dx の長さの質量 m は，ρdx となるので，1 波長内（ 0 ～λ）の運動エネルギー K は，
　　　　　　　
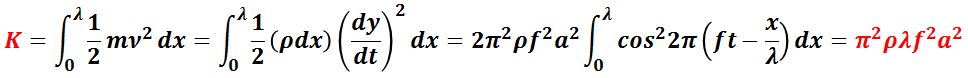
となる。
　
　位置エネルギー
　波動が無いときの気体の圧力を P₀ とする。断面積 1 ，長さ l のシリンダーに気体を入れ，外から力 F を加え，ピストンを極わずかな量（η）だけ動かしたとする。気体の比熱比γのとき加えた力 F は，
　　　　　　　
となる。
　ηが任意の値（ただしη/l ≪1 ）になるまでの仕事は，
　　　　　　　
である。
　ここで，シリンダーを空間の中の単位断面積の dx 離れた気柱とすると，音波によるある瞬間の変位がηと考えられるので，
　　　　　　　
と置けるので，dx の部分が伸び縮みして蓄える位置エネルギー（仕事）として，
　　　　　　　
がえられる。従って，振動数 f （波長λ），振幅 a の音波の 1 波長内の位置エネルギー U は，
　　　　　　　
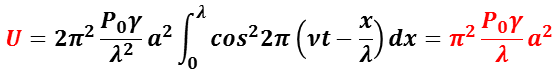
となる。前述したように，音速と圧力，気体の密度の関係は，
　　　　　　　
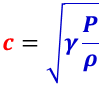
で与えられるので，
　　　　　　　
と，運動エネルギー K と等しい値になる。従って，1 波長内の音のエネルギー E は，
　　　　　　　
が得られる。
　従って，単位時間当たりのエネルギー I は，
　　　　　　　
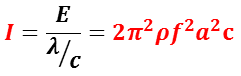
となる。この単位時間当たりのエネルギーを音の強さという。
　以上をまとめると，“音の強さは，音波の振幅の二乗と振動数の二乗に比例する”ことが分かる。