物理 第五部:熱力学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,物質と熱の関係(相転移,熱の移動)について, 【三態(相)と相図】, 【相転移とは】, 【熱移動・熱伝導】, 【熱移動・熱対流】, 【熱移動・熱放射】, 【プランクの法則】, 【熱伝達とは】 に項目を分けて紹介する。
【三態(相)と相図】
物質の曝される温度,圧力などの環境条件を変えると,物質の状態が変化(固体⇔液体⇔気体など)することは日常生活の中で経験される。
固体,液体,気体などの物質の状態をまとめて物質の三態(three states of matter)や三相(three phases of matter)と呼ぶ。
なお,物質の三態が同時に安定的に共存する温度は三重点(triple point)と呼ばれる。また,物質の相と温度・圧力などの熱力学的な状態量との関係を表したものを相図(phase diagram)や状態図という。
物質の三相の一般的な特徴は,次の通りである。
固体( solid )
液体と比較して変形や体積変化が極めて小さい。固体を構成する粒子(原子,分子やイオン)は,粒子間の相互作用(引力)により粒子(原子や分子)の位置がほぼ固定され,移動が制限される。粒子が規則正しい繰り返しで並ぶ場合(結晶)と不規則に並ぶ場合(アモルファス)がある。
液体( liquid )
流動的で容器に合わせて形を変えることができる。液体は気体と異なり,粒子間の相互作用(引力)が比較的弱く,粒子(原子や分子)の位置は固定されず,自由に流動できるが,粒子間の距離がほぼ一定に保たれるため容器全体に広がることが無い。また,圧縮性が小さいので,ほぼ一定の密度を保つ。一般的に,液体の密度は,固体の密度に近く,気体より著しく高い。
気体( gas )
一定の形と体積を持たず,自由に流動し,圧縮やずれに対する抵抗が小さく,圧力の増減で体積が容易に変化する状態である。また,外部から力を受けない状態では,気体の体積が無限に膨張する。
気体を構成する粒子(原子や分子)は,自由かつランダムに動く熱運動をしている。気体の粒子は,それぞれ離れているため,粒子間には引力(分子間力)が働かない。
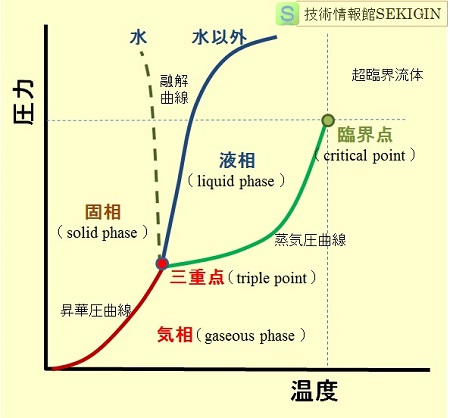
物質の相図(模式図)
相図とは
相図には,選択する状態量に応じて,合金や化合物の温度,圧力,組成に関する相図,磁気構造と温度との関係を示す相図など様々ある。
下図に例示する物質の三相と温度,圧力の相図(模式図)では,液相と固相の境界を融解曲線(melting curve),気相と固相の境界を昇華圧曲線(sublimation curve ,昇華曲線),気相と液相の境界を蒸気圧曲線(vapor pressure curve ,蒸発曲線)といい,三つの曲線が交わる点を三重点(triple point)という。
模式図において,蒸気圧曲線が高温高圧側で途切れているのは,それ以上の高温高圧では超臨界流体(supercritical fluid)になることを意味し,この点を臨界点(critical point)という。
超臨界流体とは,気体の拡散性と液体の溶解性を併せ持ち,気体と液体の区別がつかない状態をいう。
一般的に,多くの物質の融解曲線は,圧力の増加と共に固体の融点が高くなる。しかし,水素結合で凝集する水やアンモニアなどの一部の物質の固体は,圧力の増加で融点が低くなるなど特異な現象を示す。
【参考:基礎用語】
- 分子間力(intermolecular force)
分子間力とは,電気的に中性の分子間に作用する力で,気体から液体や固体への相転移で重要な役割を果たす。
液体における一般的な力は,“ファンデルワールス力”で,液体の特性や固体の結晶化などでは“双極子に基づく力”,原子間の電気陰性度に大きな差があり,大きい双極子モーメントが発生する構造を持つ特定の分子(水やアンモニアなど)では“水素結合”が主要な力として働く。 - 水素結合( hydrogen bond )
分子間に水素を介して働く力を水素結合という。周期表 第 2 周期の元素(炭素,窒素,フッ素)の水素化物は,分子量が小さいにもかかわらず,同族元素の第 3 周期の元素より異常に高い沸点,融点を有する。このことは,これらの分子にファンデルワールス力以外の強い分子間力(水素結合)が働いていることを示す。
ページの先頭へ
【相転移とは】
上記の「相図とは」で紹介したように,物質の三相(気相,液相,固相)は,温度や圧力を変えることで,相互に変化する。この変化を相転移(phase transition)や相変態(phase transformation)といわれる。なお,次に示すように,相転移は,一次相転移と二次相転移に分けられる。
一般的に相転移という場合は,物質の三相間の相互転移などエントロピーや体積などの値が両相で有限の差をもつような一次相転移をいう。
他に,鉄鋼の相転移で紹介されるように,固体であっても温度や圧力により結晶構造の違いなど複数の相を作る。
これらの相の間での転移,磁性体における常磁性-強磁性転移,合金の秩序無秩序転移,液体ヘリウムの λ 点における正常流体から超流動流体への転移など定圧比熱容量や等温圧縮率の値に有限の差をもつような相転移があり,これを二次相転移という。
一次相転移の概要
固体 ⇔ 液体
① 固体⇒液体
固体が液体に変わる現象を融解(melting , fusion)といい,変化している間は,熱を与えても温度が一定に保たれ,この温度を融点(melting point)という。固体が液体に変化するときに吸収する熱エネルギー(潜熱)を融解熱(heat of fusion)という。融解現象は,次のように説明される。
粒子(原子,分子)で構成される固体は,粒子間の距離が小さく,引力(ファンデルワールス力など)で規則正しく配列している。
固体を熱することで,粒子の熱振動が激しくなり,固体表面の粒子の一部が引力に抗して配列の崩れから流動を開始(液体に変わる)する。
粒子の配列が徐々に崩れてゆくが,外から与えられたエネルギーがこのために消費されるので,固体がすべて液体に変わるまでの温度はほぼ一定に保たれる。
② 液体⇒固体
液体から熱を奪う(冷やす)場合は,固体 ⇒ 液体の逆の過程を経て固体に変わる。
液体から固体に変わる現象を凝固(freezing , solidification),又は固化(solidification)といい,変化している間は,熱を奪っても温度が一定に保たれ,この温度を凝固点(freezing point)という。通常は融点と同じである。
一般的に,水の場合は氷結という。温度変化のみで凝固する場合を特に凍結ともいう。凝固には,融解熱と同じ量の熱エネルギー(潜熱)を放出する。これを凝固熱(heat of solidification)という。
固体 ⇔ 気体
① 固体⇒気体
固体が液体を経ずに気体に変わる現象を昇華(sublimation),又は気化(vaporize)といい,変化している間は,熱を与えても温度が一定に保たれ,この温度を昇華点(sublimation point)という。昇華のときに吸収するエネルギー(潜熱)を昇華熱(heat of sublimation)という。昇華現象は,次のように説明される。
固体を熱することで,粒子の熱振動が激しくなる。融解の場合と異なり,表面近くの一部の粒子が引力を振り切り,直接上部の空間に飛び出す(気体に変わる)。
なお,常温の大気圧でこの現象が観察される物質には,よう素,ドライアイス(二酸化炭素),防虫剤に用いられるナフタレンや樟脳(しょうのう),トイレ消臭剤ブロックに用いられるパラジクロロベンゼンなどがある。フリーズドドライは,氷の昇華現象を利用した技術である。
② 気体⇒固体
固体⇒気体と逆の現象も昇華といわれる。固体からの昇華と区別したい場合には,凝固や凝結と呼ばれることがある。昇華現象は,次のように説明される。
気体から熱を奪うことで液体を経ずに固体・気体間を直接相転移する現象は,粒子間の引力が小さい物質で起こりやすい。
この現象は,相図で,圧力と温度の交点が三重点より下になった時に起きる。
液体 ⇔ 気体
① 液体 ⇒ 気体
液体が気体に変わる現象を蒸発(evaporation),又は気化(vaporize)という。熱を与え続けると,蒸発と共に液体の温度も上昇するが,ある温度に至ると熱を与えても温度の上昇が止まり,容器界面などからも激しく蒸発し始める。この温度を沸点(boiling point)という。蒸発するときに吸収するエネルギー(潜熱)を蒸発熱(heat of evaporation),又は気化熱という。蒸発現象は,次のように説明される。
液体に熱を与えることで,粒子の熱運動が激しくなる。運動エネルギーの大きい粒子が粒子間の引力を振り切り,液体表面(又は界面)から空間に飛び出す(気体に変わる)。
液体の温度が高い場合には,粒子間の引力を振り切れる粒子の数が増え,激しい蒸発が起き,ついに蒸気圧が環境の気圧と等しくなると,液体表面以外に容器壁との界面などからの蒸発(沸騰)に至る。
② 気体⇒液体
気体が液体に変わる現象を 凝縮(condensation),又は液化(liquefaction)という。他に,凝結や結露などともいわれる。凝縮する際に放出されるエネルギー(潜熱)を 凝縮熱(heat of condensation)という。凝縮現象は,次のように説明される。
気体から熱を奪うことで,粒子の運動エネルギーが次第に小さくなり,粒子同士の衝突や液体表面への衝突時に,粒子間の引力に捕えられ液体になる。
【参考:基礎用語】
- 潜熱(latent heat)
転移熱(heat of transition)といもいい,物質が温度を変えないで,相転移するために吸収または発生する熱をいう。すなわち,相転移が進行中の温度が一定のままとなる。例えば,融解熱,凝固熱,凝縮熱,蒸発熱,昇華熱などがある。 - エントロピー(entropy)
系の微視的な「乱雑さ」を表す指標として,伝統的にはクラウジウスの不等式(Σ( Qi / Ti ) ≦ 0 )を用いて定義している。エントロピーの次元は,エネルギーを温度で割った次元(単位:ジュール毎ケルビン)をもつ。 - 定圧比熱容量(specific heat capacity at constant pressure)
圧力一定の条件で,単位質量の物質を単位温度上げるのに必要な熱量をいう。単位は J・kg‐1・K‐1 である。
なお,一般的には,液体や固体の体積は,温度による極端な変化はないが,気体は,温度によるエンタルピーや体積の変化が大きいため,比熱容量を表示する場合は,温度の指定が必要である。 - 圧縮率(compressibility)
物体が圧縮される難易の程度を表わす状態量で,圧縮率が大きいほど圧縮されやすいことを表す。温度が一定の条件下での圧縮率を等温圧縮率といい,断熱条件下での圧縮率を断熱圧縮率という。また,圧縮率の逆数は体積弾性率(bulk modulus),体積弾性係数などといわれる。
ページの先頭へ
【伝熱(熱移動)・熱伝導】
伝熱(熱移動)
熱エネルギーが,ある場所から他の場所に移動する現象を熱移動(heat transfer)や伝熱(heat transfer)という。ちなみに伝熱は,熱の移動現象を扱う熱工学の一分野でもある。
温度勾配を駆動力とする伝熱の基本現象は,例えば,固体の内部や固体と固体とが接触している場合の熱伝導(heat conduction),気体や液体の分子の移動によって熱を運ぶ熱対流(heat convection),電磁波の授受で熱エネルギーが移動する熱放射(thermal radiation)に分けられる。
しかし,それぞれの現象が単独で作用する場合はまれで,液体と固体の接触など,実用面の熱の授受は,熱伝導と熱対流が関連した複雑な現象である。この現象を扱う場合は,熱伝達(heat transfer)という。
熱伝導
伝熱過程の 1 種で,物質の移動を伴わず,物質間の接触個所を通して,高温側から低温側へ温度勾配を駆動力として熱が移動する現象を熱伝導という。伝熱における熱伝導の寄与は,気体や液体では小さく,固体で大きい。
固体の熱伝導は,固体を構成する原子の振動,結晶格子の振動や伝導電子の振動を介して行われる。
一般的には,伝導電子の寄与が大きいので,金属の熱伝導性は半導体や絶縁体よりも良い。しかし,ダイヤモンドは例外で,結晶格子間を伝わる振動(フォノン)を介した熱伝導性の寄与が非常に大きく,金属より熱伝導性が良い。
熱伝導の難易の程度を表わす量を熱伝導率(thermal conductivity)という。熱伝導率は,フーリエの法則の比例係数λとして定義されている。
フーリエの法則(Fourier's law)
長さ dx で温度差 dt の物体において,熱の流れに垂直な面を通る熱量 q は,温度勾配( dx/ dt )と断面積( A )に比例し,
![]()
で表される。
熱伝導率の記号には,λ,κが用いられ,SI単位はワット 毎 メートル 毎 ケルビン (W・m‐1・ K‐1 )である。
主な材料の熱伝導率(W・m‐1・ K‐1)
ダイヤモンド( 1000 ~ 2000),銀( 0 ℃,428 ),銅( 0 ℃,403),金( 0 ℃,320),アルミニウム( 0 ℃,236),鉄( 0 ℃,83.5),白金(70),ステンレス鋼(17 ~ 20.9),氷( 0 ℃,2.2),ガラス( 0 ℃,0.55 ~ 0.75),水( 0 ℃,0.582),木材(室温 0.15 ~ 0.25),空気( 0 ℃,0.0241)
出典
青字の材料:大塚徳勝著:「そこが知りたい物理学」共立出版(株) 1999年
黒字の材料:インターネット検索による引用,引用元は不明
ページの先頭へ
【伝熱・熱対流】
流体(気体や液体)の巨視的な流れに伴い,流体の熱エネルギーや溶存物質などが運ばれる現象を対流(convection)や移流(advection)ともいう。熱の流れに注目した場合は,熱対流や対流伝熱という。
外力を与えて起こした対流を強制対流,流体内部の温度差,密度差,重力,表面張力などの自然の作用により自発的に起きる対流を自然対流と呼んで区別することもある。
自然対流には,流体の上層ほど密度が大きく,流体の上下方向の運動が生ずる鉛直対流,流体に水平方向の温度差が与えられた場合に水平方向の運動が生じる水平対流,不均一な表面張力で流体の流れが駆動されるマランゴニ対流などがある。
鉛直対流
温度による流体の密度の変化が原因となる対流で,最も一般的な熱対流である。鉛直対流では,流体内部に半定常的な細胞状の模様(対流セル)が形成されることがある。この熱対流はレーリー=ベナール型対流とよばれ,対流セル中心付近では上昇流,セル境界付近では下降流になっている。
水平対流
地球において,緯度の違いによる温度差で生じる大気大循環,大陸と海洋の温度差で生ずる季節風,海岸地域での地表面と海面の温度差による海陸風,都市部のヒートアイランド現象で生じる郊外風などが水平対流の例である。
ページの先頭へ
【伝熱・熱放射】
熱放射(thermal radiation)は,物体の熱を電磁波として放出する現象をいい,熱輻射(temperature radiation ,thermal radiation),単に輻射(radiation)ともいう。
熱放射による伝熱は,輸送元の物体が電磁波を出し,輸送先の物体がそれを吸収することで達成される。熱放射による伝熱は,宇宙空間のように,物体間の熱伝導,熱対流が期待できない真空であっても熱を伝えることができる。
物体の熱放射は,プランクの放射則(Planck's law)で知られる黒体からの熱放射が原理となる。すなわち,プランクの放射則では,物体の放射する電磁波の波長とその分布が熱力学(的)温度のみに依存することを示している。
実際の物体が出す熱放射は,黒体放射よりも小さいので,実際の物体が出す熱放射/黒体放射の比を射出率または放射率(emissivity)εを用いて比較できるようになっている。
熱放射で運ばれる熱量
相対する 2 の物質( A , B )の放射率をεA ,εB ,相手の物質に向く面の表面積を SA , SB ,温度を TA >TB とした時,物体 A から物体 B に運ばれる熱量 P は,
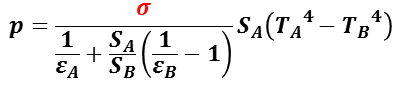
で与えられる。ここで,σ はシュテファン=ボルツマン定数である。
表面積が SA ≪ SB の関係にあるとき(点熱源,太陽と地球の関係など)は,
![]()
で表される。
シュテファン=ボルツマン定数
ヨーゼフ・シュテファン(1835 ~ 1893 年)が黒体から熱放射される電磁波のエネルギー( I )と熱力学(的)温度( T )の関係( I = σ T4 )を実験的に明らかにし,その後にルートヴィッヒ・ボルツマン(1844 ~ 1906年)が理論的に解明したため,この関係をシュテファン=ボルツマンの法則(Stefan-Boltzmann law)という。
比例定数σは,シュテファン=ボルツマン定数といわれ,プランクの法則により他の普遍定数と理論的に関係付けられている(CODATA2014推奨値)。
![]()
ここで c :真空中の光の速度,h :プランク定数,k :ボルツマン定数
放射率(emissivity)
放射率は,物体が熱放射で放出するエネルギー(放射輝度)と同温の黒体が放出するエネルギーの比( 0 ~ 1 の間の値)で記号εが用いられる。放射率は,物質種,光の波長で異なる。
物体に電磁波が当たった時に,その電磁波のエネルギーの内, 物体に吸収されるエネルギーの割合は吸収率(absorptance)α,物体に吸収されず透過したねるぶぎーの割合を透過率(transmittance)τという。物体から反射されるエネルギーの割合を反射率(reflectance)R という。
これらの関係は,次の通りである。
ε=α :キルヒホッフの法則(Kirchhoff's laws)
R+τ+α= 1 :エネルギー保存則
ここで,物体が不透明であれば,透過率τ= 0 となり,
R + α= 1 ,R +ε= 1
の関係が得られる。すなわち,反射率の小さい物質ほど,放射率ε,吸収率αが大きいことが分かる。
【参考:基礎用語】
- シュテファン(Joseph Stefan)
ヨーゼフ・シュテファン(1835年 ~ 1893年)は,オーストリアの物理学者,数学者で,シュテファン=ボルツマンの法則で知られるボルツマンの師である。 - ボルツマン(Ludwig Eduard Boltzmann)
ルートヴィッヒ・エードゥアルト・ボルツマン(1844年~1906年)は,オーストリア・ウィーン出身の物理学者,哲学者。統計力学,電磁気学,熱力学,ボルツマンの関係式,ボルツマン定数などで知られる。 - キルヒホッフの法則(Kirchhoff's law)
ドイツの物理学者グスタフ・ロベルト・キルヒホフ(1824年 ~ 1887年)が発見した法則に対する一般的な呼称であるが,技術分野の異なる次の 3 つの法則がある。
一つは,電気分野の電気回路の電流と電圧に関するキルヒホッフの法則(電気回路)
二つ目は,電磁波分野の黒体放射など局所熱平衡状態で成り立つ,光と物体の相互作用に関するキルヒホッフの法則(放射エネルギー)
三つ目は,熱化学分野の反応熱の温度係数が反応前後の熱容量の差に等しいというキルヒホッフの法則(反応熱)である。 - キルヒホフ(Gustav Robert Kirchhoff)
グスタフ・ロベルト・キルヒホフ(1824年 ~ 1887年)は,プロイセン生まれのドイツの物理学者で,キルヒホッフの法則(電気回路,放射エネルギー,化学反応熱),分光学,音響学で知られる。 - エネルギー保存の法則(law of the conservation of energy)
“閉じた系(外界とエネルギーの出入りが無い系)において,エネルギーの移動,形態の変更などによっても,その総量が変化しない”と定義され,物理学における保存則(conservation law)の一つで,短縮してエネルギー保存則ともいわれる。
19 世紀までに力学的エネルギー保存の法則(principle of mechanical energy)が確立され,その後に熱現象も含めた熱力学の第一法則(孤立系のエネルギーの総量は変化しない)がマイヤー,ジュール,ヘルムホルツらにより確立されたことで,音,光,電磁気,化学変化,原子核反応等を含めた自然現象を支配する基礎法則となった。 - プランク(Max Karl Ernst Ludwig Planck)
マックス・カール・エルンスト・ルートヴィヒ・プランク(1858年~1947年)は,ドイツの物理学者。量子論創始者の一人で,「量子論の父」とも呼ばれている。
ページの先頭へ
【プランクの法則】
プランクの法則(Planck's law)は,プランクの放射則,プランクの放射法則(Planck's law of radiation),プランクの公式などとも呼ばれ,1900 年にドイツの物理学者マックス・プランク(1858 ~1947 年)が導いた黒体から輻射(放射)される電磁波の分光放射輝度又はエネルギー密度の波長分布に関する公式である。
JIS Z 8120 「光学用語: Glossary of optical terms 」では,プランクの放射則(Planck’s law)として,“黒体の分光放射輝度を波長及び温度の関数として与える法則。”と定義し,備考欄に“次の式によって表される。”としている。
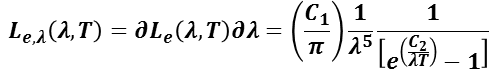
ここに,Le :放射輝度,λ:真空中の波長,T :黒体の熱力学(的)温度(K),h :プランク定数,c :真空中における光の速さ,k:ボルツマン定数
参考
1. C1 及び C2 の CODATA(科学技術データ委員会) 1998 推奨値
C1=2πhc2= (3.741 771 07±0.000 000 29) ×10−16 W・m2
C2=hc/ k= (1.438 775 2±0.000 002 5) ×10−2 m・K
2. ITS-90(International Temperature Scale of 1990)での推奨値,C2=14 388 µm・K としている。
黒体(blackbody)
プランクの放射体(Planckian radiator)ともいわれ,JIS Z 8120 「光学用語」で“波長,入射方向,偏光のいずれにもかかわりなく,入射するあらゆる放射を完全に吸収する理想的な熱放射体。備考 黒体は,いかなる波長,いかなる方向においても,同じ温度で熱平衡状態にある熱放射体のうちで最大の分光放射輝度をもつ。”と定義されている。
放射輝度(radiance)
JIS Z 8120 「光学用語」では,“放射が伝わる経路上の断面(発生面及び到達面を含む。)の単位面積当たり,かつ,経路方向の単位立体角当たりの放射束。”と定義している。
放射では,波長(又は周波数)毎の放射輝度を考えることができ,これを分光放射輝度やスペクトル放射輝度とよぶ。
分光放射輝度(spectral radiance)
JIS 規格のプランクの放射則の解説では,分光放射輝度( Le )を波長(λ)と温度( T )の関数で表したものであるが,周波数(ν)で表すと,
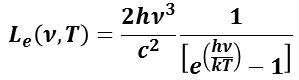
となる。
この式から分かるように,分光放射輝度は,温度 T で決まる周波数をピークとし,高周波数側は指数関数的に,低周波数側は多項式的に減少する分布を示す。
ちなみに,大気環境での一般的な温度範囲を 10~50℃とすると,放射される電磁波のピークの波長は約 9~10 μmとなる。これは,一般的な遠赤外線( 8μm以上)の領域である。
ページの先頭へ
【熱伝達とは】
実環境における伝熱は,きわめて複雑な過程を含む。
例えば,大気中に高温の金属体を置いた場合に,金属と接触する空気との間の熱伝導,熱せられた空気の自然対流に加えて,金属からの熱放射が同時に起きる。
それぞれの現象を詳しく考察することも可能であるが,非常に複雑な問題を解くことになる。
そこで,この現象全体を巨視的に捉えた熱伝達(heat transfer)の解を求める近似法が提案されている。
ニュートンの冷却の法則(Newton's law of cooling)
“固体と流体との温度差があまり大きくないとき( 50 K 以内)には,固体表面とこれに接する流体との間の熱の出入りは,両者の温度差に比例する。”
アイザック・ニュートン(1642 ~ 1727 年)が提案した経験則である。熱伝達に関する基本となる近似のため,第一近似ともいわれる。
この近似は,固体表面での熱の出入りが一様に起きていると考えられる場合に適用される。
固体の表面積 A ,温度T,固体から十分に離れた位置での流体の温度 T0 とした時,時間 ⊿ t の間に固体から流体に流れる熱量 ⊿Q は,
⊿Q = h A ( T- T0 ) ⊿ t
で与えられる。ここで h は熱伝達率(heat transfer coefficient),表面熱伝達率,境膜係数(film coefficient)などといわれる。
熱伝達率(heat transfer coefficient)
熱伝達率は,対流熱伝達,沸騰熱伝達,凝縮熱伝達などの流体と物体間の熱移動を扱うための係数で,単位面積,単位時間,単位温度差あたりの伝熱量である。
これは,上述のニュートンの冷却法則を根拠としており,単位 W・ m‐2・ K‐1 ,記号には,h やαが用いられる。
なお,熱伝達率は流体の速度によっても大きく異なるが,物体(固体)の表面形状や流体の流れが一様ではない実用面において,平均値としての熱の移動を扱う工学的な問題で有用な係数として扱われる。
熱伝達率は,強性対流,自然対流,物体の形状(円管,円柱,水平平板,垂直平板など)に応じて,多くの計算式が提案されている。
熱伝達率の計算では,物体の代表的長さ( L ),体膨張係数(γ),流体の流速( U ),密度(ρ),粘度(η),動粘性係数(ν=η/ρ),定圧比熱容量( Cp ),熱伝導率(λ)などの物性値の他に,流体力学で慣性力と粘性力との比で定義されるレイノルズ数(Reynolds number :記号 Re ),流体の動粘度と温度拡散率の比で定義されるプラントル数(Prandtl number :記号 Pr ),流れ場における粘性力に対する浮力の相対的な影響を示すグラスホフ数(Grashof Number :記号 Gr ),グラスホフ数とプラントル数の積であるレイリー数(Rayleigh's number :記号 Re ),対流による熱伝達と流体(静止している流体)の熱伝導の比を表すヌセルト数(ヌッセルト数,Nusselt number :記号Nu ),熱伝達率と熱容量の比を表すスタントン数(Stanton number :記号 St )が用いられる。
例えば,多数ある実験的,理論的な式の中から強制対流での熱伝達率の計算式の一例を次に示す。
![]()
ページの先頭へ