物理 第一部:物理学とは
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,古典物理学(力と運動)の基本について,【ニュートン力学とは】,【ベクトルとは】,【速度と速さ】,【加速度・重力加速度】,【重さ(重量)と質量】に項目を分けて紹介する。
【ニュートン力学とは】
ニュートンは,ガリレイの相対性原理(Galilean principle of relativity)の要請を満たす物体に働く力と運動の関係を扱う力学(二―トン力学)を完成させた。
ニュートン力学(Newtonian mechanics)とは,「絶対時間」と「絶対空間」を前提とし,ニュートンの運動の法則(運動の第1法則,第2法則,第3法則),万有引力の法則など二体間に働く力を基礎とした力学体系で,古典力学(classical mechanics)ともいわれる。
特殊相対性理論の登場で覆されたが,ニュートンが前提とした絶対時間と絶対空間は,次の様に考えられていた。
絶対時間(absolute time)
“絶対的な・真の・数理的な時間とは,外部と一切かかわりなく,おのずとその本質に基づいて一律に流れていくものである。”とし,観察者とは無関係に,宇宙のいかなる場所でも一定の早さで進むもので,数理的に理解するもので,知覚できないものである。すなわち,人間が知覚できるのは相対時間である。
絶対空間(absolute space)
“外部と一切かかわりなく、本質として不変不動を保つものである。”とし,人間の知覚する空間は,諸物体に対する位置として相対空間である。
ニュートンの運動の法則(law of motion)とは,物体を重心に全質量が集中し,大きさをもたない点(質点)と仮定し,次の 3 法則をいう。
第1法則(慣性の法則:law of inertia)
外から力が作用しない限り,質点は静止または等速直線運動する。
第2法則(ニュートンの運動方程式:Newton's equation of motion)
質点の加速度 a は,そのとき質点に作用する力 F に比例し,比例定数 m に反比例する ma=F 。比例定数 m が質点の質量(慣性質量)である。
第3法則(作用・反作用の法則:law of action and reaction)
二つの質点 A , B の質点 A から質点 B に力(作用)を及ぼすと,同時に質点 B から質点 A に力(反作用)が及ぼされ,作用と反作用は大きさが等しく逆向きである。
万有引力の法則(law of universal gravitation)
ニュートンは,太陽を公転する地球の運動や木星の衛星の運動の説明を試み,ケプラーの法則(Kepler's laws)に運動方程式を適用し,引力(重力)が 2 つの物体の質量(重力質量)に比例し,距離の2乗に反比例することを証明した。
すなわち,質量を持つ物質が引力を持つという法則で,距離 r だけ離れた二つの質点(質量 m1 ,m2)の間に働く引力 F は,
F = G・m1・m2・r-2
で与えられる。
比例定数 G を万有引力定数(重力定数)といい, CODATA(科学技術データ委員会: Committee on Data for Science and Technology)の2014年の推奨値は,G = 6.674 08(31)×10-11(Nm2kg-2)である。
地球の質量は,万有引力の法則を用いて求められ, 5.972 × 1024 kg と計算されている。
アインシュタインの一般相対性理論では,万有引力は,ニュートン力学的な力ではなく,重力場の方程式(アインシュタイン方程式)で表される重力場という時空の歪みと説明される。
このため,質量を持った物体間の力ではなく,質量を持たない物質(例えば光)も重力によって曲がる事を意味し,実際の観測で実証されている。
しかし,光速度に近い高速度の運動を問題としない限り,すなわち,太陽系での一般的な現象であれば,ニュートン力学に若干の補正項が加わる程度の違いしかないので,ニュートン力学は近似的に正しいと考えて実用上の支承はない。
【参考:基礎用語】
- ケプラーの法則(Kepler's laws)
ヨハネス・ケプラーが発見し惑星の運動に関する法則。過去の観測記録などから太陽に対する火星の運動を定式化した次の 3 つの法則をいう。
第1法則(楕円軌道の法則:1609年)
惑星は,太陽をひとつの焦点とする楕円軌道上を動く。
第2法則(面積速度一定の法則:1609年)
惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である(面積速度一定)。
第3法則(調和の法則:1619年)
惑星の公転周期の2乗は,軌道の長半径の3乗に比例する。 - ヨハネス・ケプラー(1571年 ~ 1630年)
ドイツの天文学者で,天体の運行法則を唱え,理論的に天体の運動を解明したことで知られる。天体物理学の先駆的存在といわれている。 - キログラム原器
1875年成立のメートル条約に基づいて1880年に白金 90%,イリジウム 10%の合金で作られている。1889年の国際度量衡総会で国際原器として認証されたもので,フランスの国際度量衡局に保管されている。国際キログラム原器の複製品が各国キログラム原器として配布され,日本国キログラム原器(No.6)は,独立行政法人産業技術総合研究所計量標準総合センターに保管されている。
ページの先頭へ
【ベクトルとは】
運動を考える上で,力や速度を表すのに大きさの他に方向が重要な要素になる。このため,ベクトル(vector)で考えるのが通例である。なお,長さ,時間,質量,熱量などの方向を示すことの意味がなく,すなわち特定の座標系とは無関係の量をスカラー(scalar)という。なお,あえてスカラー(量)と明記するのは,ベクトルと対比して議論する場合である。
ベクトルには,平面上で方向と大きさで規定される量の平面ベクトルと空間における方向と大きさで規定される量の空間ベクトルに分けられる。単にベクトルという場合は,平面ベクトルを指すのが通例である。
平面ベクトルの成分表示は(X 成分,Y 成分)の二次元表示で,空間ベクトルでは(X 成分,Y 成分,Z 成分)の三次元で表示される。
ベクトルを表す記号
ベクトルの記号は,通常の記号と区別できるように,記号の上に矢印を付ける表示方法,太字で書いて区別する方法が採られる。一般的には,分かり易い表示として矢印を付ける表示法が用いられることが多い。
有効線分とベクトルの違い
有向線分(oriented segment)
平面上の 2 点(X , Y)として,点A(2 , 3)と点 B(7 , 6)があり,2 点間を結ぶ線は,点 A を出発点とする場合と点 B を出発点とする場合で,線分の長さは同じであるが方向が逆となる。
この場合に,線分 AB としたのでは方向が明確でないため,点 A を出発点とする線分を![]() ,点 B を出発点とする線分を
,点 B を出発点とする線分を![]() と表記することで,異なる線分
と表記することで,異なる線分![]() ≠
≠![]() を明らかにできる。このように,始点と終点の場所を指定し記号の上に矢印を付けた表記を有向線分という。
を明らかにできる。このように,始点と終点の場所を指定し記号の上に矢印を付けた表記を有向線分という。
ここで,下図に示すように,有向線分![]() を X 軸方向に 5 ,Y 軸方向に 2 だけ平行移動する。
を X 軸方向に 5 ,Y 軸方向に 2 だけ平行移動する。
すなわち,出発点C(4 , 5)と終点 D(9 , 8)の有向線分![]() が得られ,それぞれは起点の位置が異なる有向線分
が得られ,それぞれは起点の位置が異なる有向線分![]() ≠
≠![]() として扱われる。
として扱われる。
ベクトル(vector)
ベクトルは,有向線分と異なり,平面上の位置に依存せず,大きさと向きだけを持つ量である。例えば,有向線分![]() をベクトル
をベクトル![]() ,有向線分
,有向線分![]() をベクトル
をベクトル![]() とする。
とする。
この時,ベクトルの成分は,起点と終点の X 軸の位置の差と Y 軸の位置の差で表されるので,ベクトル![]() のX 軸の位置の差 5(= 7-2),Y 軸の位置の差 3(= 6-3)となり,ベクトル
のX 軸の位置の差 5(= 7-2),Y 軸の位置の差 3(= 6-3)となり,ベクトル![]() のX 軸の位置の差 5(= 9-4),Y 軸の位置の差 3(= 8-5)と同じ,すなわち向きと大きさが等しいので,ベクトルは等しく
のX 軸の位置の差 5(= 9-4),Y 軸の位置の差 3(= 8-5)と同じ,すなわち向きと大きさが等しいので,ベクトルは等しく![]() =
=![]() となる。
となる。
なお,有向線分![]() のベクトル表示での成分は,X 軸の差-5(=2-7),Y軸の差 -3(= 5-8)で,大きさが同じで向きが反対のベクトル -
のベクトル表示での成分は,X 軸の差-5(=2-7),Y軸の差 -3(= 5-8)で,大きさが同じで向きが反対のベクトル -![]() となる。
となる。
ベクトルの大きさだけ,すなわち絶対値を表す場合は,例えば|![]() |(=
|(=![]() )と表示する。
)と表示する。
ベクトルの演算
ベクトルとベクトルの和と差
ベクトルは,大きさと方向が維持できる平行移動が可能である。従って,ベクトル![]() の起点を O に置いた時,終点の A にベクトル
の起点を O に置いた時,終点の A にベクトル![]() の起点を合わせ,終点を P とする。この時,点 O と P を結ぶベクトル
の起点を合わせ,終点を P とする。この時,点 O と P を結ぶベクトル![]() 和ベクトル(合成ベクトル)といい,
和ベクトル(合成ベクトル)といい,![]() =
=![]() +
+![]() と書く。ベクトルを入れ替えてもこの関係が成り立つ,すなわち,OP が平行四辺形OAPBの対角線になっている。この関係は平行四辺形の法則といわれる。
と書く。ベクトルを入れ替えてもこの関係が成り立つ,すなわち,OP が平行四辺形OAPBの対角線になっている。この関係は平行四辺形の法則といわれる。
ベクトルを実数(λ)倍することができる。これをスカラー倍という。λが正のときは同方向のベクトルを,負のときは逆方向のベクトルを示す。
ベクトルとベクトルの差は,下図に示すように,一方のベクトルをλ=‐1 倍(同じ大きさで逆方向のベクトル)したものとの和ベクトルを得ることを意味する。
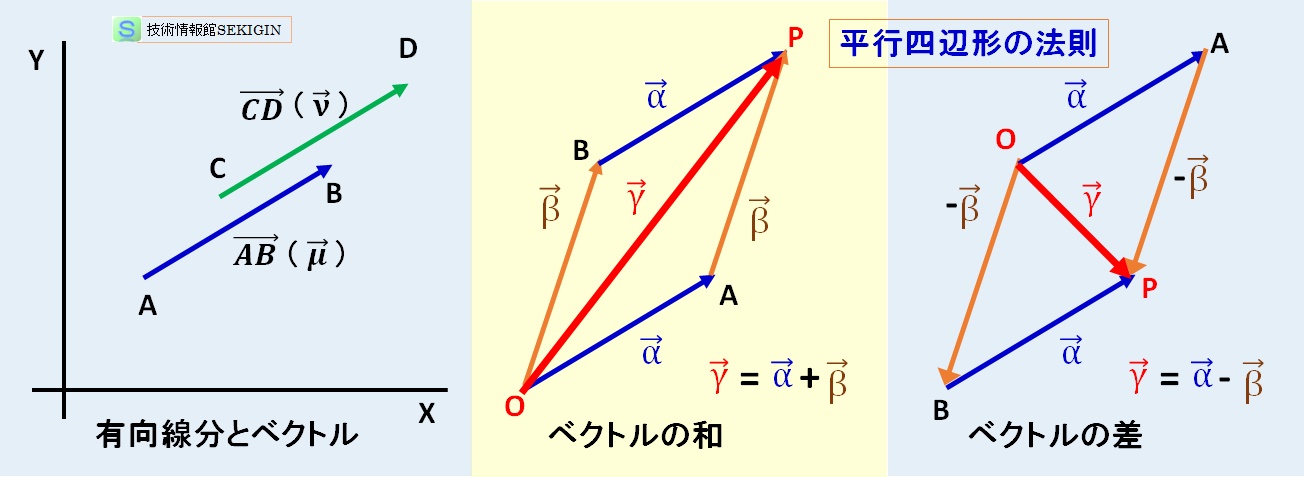
有向線分・ベクトルの表示と和・差
ページの先頭へ
【速度と速さ】
速さ(speed)
移動体が計測された時間間隔で進む距離である。
後述の速度は,単位時間当たりの物体の位置の変化量と定義され,速さと速度は異なる定義の用語であるが,日常用語として速度を速さと誤用する例が多い。
速度(velocity)
単位時間当たりの物体の位置の変化量である。
絶対値の単位は,速度,速さとも距離(m)÷時間(s) であるが,速度は移動方向を表すベクトル量で,速さは移動方向を含まないスカラー量である。
速度(velocity)は,位置の変化量以外に,着目する現象の時間的に変化に対しても拡大使用され,面積速度(face velocity),角速度(angular velocity),反応速度(reaction rate)など,学術分野により種々の概念が定義されている。
例えば,面積速度は,ケプラーの法則の第2法則(面積速度一定の法則)で,惑星と太陽とを結ぶ線分が単位時間に描く面積と定義している。
角速度は,質点は大きさを持たないが、一般の物体は大きさを持つため,回転運動が定義され,単位時間当たりの回転量と定義される。
反応速度は,化学反応の反応物あるいは生成物に関する各成分量の時間変化率と定義されている。
ページの先頭へ
【加速度・重力加速度】
加速度(acceleration)
単位時間当たりの速度の変化率をいう。なお,速度はベクトル量のため,加速度もベクトル量になる。
位置ベクトルが時間の関数として与えられた場合には,(瞬間の)速度は位置ベクトルを時間で微分することで求められ,(瞬間の)速度を時間で微分すると加速度が求められる。
加速度もベクトルの平行四辺形の法則で合成,分解ができる。曲線運動する場合は,加速度を接線加速度,法線加速度に分解することが多い。
(瞬間の)速度は常に軌跡の接線方向を向くので接線加速度は速さの変化を表し,接線と鉛直方向に分解された法線加速度は運動の向きの変化を表わす。
重力加速度(gravitational acceleration)
重力(gravity)で生じる加速度をいう。重力のみが作用する物体の運動は,等価原理により物体の質量によらない。なお,重力という場合は,一般的に,地球上の物体に作用する地球の万有引力を意味する。
重力加速度の記号は,万有引力定数の記号 G と区別するため小文字の g が用いられる。
球対称の自転の影響を考えない場合の物体の質量 M ,半径 R とすると,球体表面付近での重力加速度の大きさは,万有引力の法則より,万有引力定数 G( 6.674 08(31)×10-11N・m2・kg‐2 )を用いて,
g = GMR‐2
で与えられる。
自転による遠心力を考慮した場合には,観測点の緯度により大きさや向きが変化する。大きさは,赤道で最も小さく,極で最も大きくなる。
重力加速度 g は,地球上の観測地点や地上からの距離で異なるが,一般的には,地表付近の運動を考える場合は,計測せずに,1901年の国際度量衡総会で,緯度 45度の海面上で,物体を自由落下させた時の値,すなわち地球上の中程度の値として定めた標準重力加速度(standard gravity) 9.80665 ± 0 m・s‐2 を用いる例が多い。
ページの先頭へ
【重さ(重量)と質量】
重さ(weight)
重量ともいわれ,普段に何げなく用いられる用語であるが,次に示す質量とは定義が明確に異なるので混同は禁物である。
重さは,物体に働く重力(慣性力)の大きさをいい,重力は重力加速度により異なるので,重さは物体固有の性質ではない。
すなわち,重力が異なる場所では,同じ物体でも重さは異なる。
適切に校正された分銅にかかる重力と比較して重さを計る化学天秤では,重力質量を求められるが,重力との比例関係を用いるばねばかりなどの計測結果は計測した場所の重力に影響される重量であり質量とは異なる。
質量(mass)
物体の動かし難さの度合いを表す量で,その定義は力学の歴史とともに推移している。物理学的には厳密には,運動の法則で動かし難さから定義される慣性質量(inertial mass),万有引力の法則で定義される重力質量(gravitational mass)がある。
なお,慣性質量と重力質量は,定義が異なるにもかかわらず,同一の値をとる。この経験則を等価原理(アインシュタイン提唱)というが,同じ値をとる理由は明確になっていない。
慣性質量mI
ニュートンの運動方程式において,物体に作用する力 F と加速度 a は比例関係にありことが証明され,その比例係数 mI が慣性質量である。
F=mI a
慣性質量は,物体を既知の力で引っ張ったときの加速度を調べ,比例係数を計算することで求められる。
重力質量 mG
重力(gravity)を起こす質量で,重力 FG は,地球上では,観測した場所での重力加速度 g (9.80619920 ms‐2 ≒ 9.8 N/kg)に比例し,その比例係数 mG が重力質量となる。
FG=mG g
重力質量は,同一地点で物体に働く重力と標準(キログラム原器)に働く重力との比較から求められる。すなわち,一般的には校正用標準分銅を用いて適正に校正された天秤(化学天秤)を用いて求められる。
なお,重力質量は,直感的にイメージする「重さ」を生じさせる質量である。
ページの先頭へ