物理 第四部:波・波動の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,音,光などの波に関し, 【波とは】, 【周期的運動(振動)について】, 【単振動】, 【単振動の合成】, 【減衰振動】, 【減衰振動方程式の解】 に項目を分けて紹介する。
【波とは】
物理的には空間を伝わる振動(oscillation , vibration)を波(wave)や波動(wave , wave motion)といい,両者は同じ意味合いを持つが,一般的に持たれるイメージには差異が見られる。
一般的に波という場合は,海,湖や川で風や震動で引き起こされる水面の高低運動を指す場合が多い。日常生活で波を意味する用語には,荒波(wild waves , rough sea),大波(billow),うねり(swell),寄せ波(surf),砕け波(breaker),さざ波(ripple),津波(tsunami)などがある。
なお,流体力学では,水面の高低運動の波は,重力波(gravity wave),表面波(surface wave)や水面波などという。
波動と称する場合は,水面の高低運動に限らず,空間や物体の一部において発生した振動などの変化が周囲に次々と伝わる現象を意味する場合が多い。
一般的に,波動を扱う分野では,物理現象として音や光などの振動(周期的な現象)が扱われる場合が多い。しかし,周期性は波動に必須の性質ではない。このため,波動では,振動が連続的に発生し伝搬する連続波(continuous wave),単独もしくは短い振動が伝搬するパルス波(pulse wave)に分類して扱われることが多い。
波動の性質
周期性を持つ波動を定義する物理量として,振動数,周期,振幅,波長,波数を正弦波(sine wave , sinusoidal wave)を例に紹介する。
振動数(frequency)記号 f
周波数ともいい,波動が単位時間当たりに繰り返される回数(周期 T の逆数)で,周期の逆数で,一般的には,単位 Hz(ヘルツ)が用いられる。
周期(period)記号 T
ある現象の各状態が一定の間隔で繰返し現れるとき,その間隔の最小値(振動数 f の逆数)で,一般的には,単位 s(秒)が用いられる。
振幅(amplitude)
波動の振動の大きさを表す 1 周期での/strong>最大変位量の絶対値で,振幅の単位は波動の種類によって異なる。
例えば,弦の振動,水面波などの媒質を伝わる波では長さ(m),音波などでは音圧(dB デシベル),電磁放射では電界強度 A(V/m),磁界強度 H(A/m)や電力束密度(W/m,sup>2)などが用いられる。
波長(wavelength)記号 λ
空間を伝わる波(波動)の持つ周期的な長さ,一般的には,単位 m が用いられる。
波数(wavenumber)記号 ν又は記号 k
単位長さ当たりの波の個数(波長λの逆数)で,物理化学,分光学分野では記号 ν,波動力学では記号 k が用いられる。
単位は,国際単位系(SI)で毎メートル(m‐1)となっているが,電磁波の場合は毎センチメートル(cm‐1)を意味する伝統的な単位カイザー K を用いる場合も多い。
【参考:基礎用語】
- 振動(oscillation , vibration)
物体の位置,電流の強さなどの物理量が一定時間(周期)ごとに一定の(減衰振動などではほぼ一定の)値をとるよう,規則正しく変動することをいう。 - 波(wave)
波には,物理的な意味合いの他に,比喩的,文学的にも多くの用法がある。
物理的には,重力波,水面波,波浪ともいわれる身近な波で,“風や震動によって起こる海や川の水面の高低運動。”,波動と同じ意味合いの“空間や物体の一部における振動や変化が,周囲の部分に次々に伝わっていく現象。”などで用いられる。
他には,人の波,歴史の波,いらかの波,感情の波など様々な表現に用いられる。 - 波動(wave motion)
空間のある点で生じた変化(振動など)が隣接する部分に次々と有限の速さで伝わる現象で,波ともいわれる。波動の性質は,周期,振幅,波長などで表され,反射,屈折,干渉,回折などの現象を示す。 - パルス波(pulse wave)
パルス(Pulse)は,脈動ともいわれ,短時間に急峻な変化をする信号の総称である。
物理学では,連続波の対義語としても用いられる。代表的なパルス波形には,矩形波 (方形波) ,三角波,鋸歯状波,半正弦波,ガウス波などがある。 - 正弦波(sine wave , sinusoidal wave)
波形が正弦曲線(サインカーブ,sine curve)として観測可能な周期的変化を示す波動で,数学,信号処理,電気工学やその他の分野において重要な働きをする。正弦曲線は,シヌソイド(sinusoid)とも呼ばれる。
ページの先頭へ
【周期的運動(振動)について】
振動(oscillation ,vibration)とは,物体の位置,電場,磁場などの物理量が一定時間(周期)ごとに一定の(減衰振動などではほぼ一定の)値をとるよう,規則正しく変動することをいう。
振り子の運動のように,安定な平衡点をはさんで周期的に位置が変化する運動で,平衡点に向って戻る復元力(restoring force)が働く系(振動系)で起る。
振動系はその構造によって定まった固有振動をもつ。振動系に復元力だけが働くときには自由振動(free vibration),抵抗などのように振幅を減少させる制動力も働くときには減衰振動(damped vibration)が起る。周期的な強制力が加わると強制振動(forced vibration)が起り,強制力と固有振動との振動数が一致すれば共振(共鳴,resonance)が生じる。
最も基本的な振動は,変位の時間変化が正弦関数で表わされる単振動(simple harmonic oscillation)である。一般的に観察される周期的振動は,フーリエ変換によっていくつかの単振動の重ね合せで表わされる。
【参考:基礎用語】
- 復元力(restoring force)
平衡位置から少しだけずれた物体をもとの位置に戻させる向きに働く力。例えば,振動するばねでは,ばねのフック力,振り子では,重力の接線成分が復元力となる。 - 固有振動(natural vibration)
自由に振動させたときの振動体固有の振動をいう。固有振動する系は,楽器で身近なように,その構造や内部条件で決る固有の振動数をいくつか持つ。その中で最も小さい振動数のものを基本振動(fundamental vibration)という。
ページの先頭へ
【単振動】
単振動(simple harmonic oscillation)は,調和振動や単調和振動ともいわれ,波形が正弦関数(又は余弦関数)で表わされる周期運動である。ある系が外部からの力の作用が無くとも,復元力により,その固有振動数で振動し続ける(自由振動)。
単振動は最も基本的な振動で,単振動する質点を調和振動子という。
例えば,直線上を運動する質量 m の質点が,直線上の原点からの変位 x に比例する復元力(F(x) =-kx:フックの法則)で原点に引かれる場合には,質点の時刻 t における変位 x(t) が,
x(t) = C sin(ωt+φ)
で単振動する。ここに,振幅 C ,角振動数ω,初期位相δ,位相角(ωt+δ)である。
この単振動は,縦軸に変位,横軸に時間をとると,正弦曲線を描くので,正弦波といわれる。
フック力による単振動では,角振動数ω( rad/ s )と周波数 f(Hz),ばね定数 k(Nm‐1),周期 T(s)とは,
f = ω/ 2 π= ( k/ m )1/2 / 2 π, T = 1/ f
の関係がある。
単振動の運動エネルギー K(x) は,
K(x) = 1/ 2・ω2 C2 cos2 (ωt + φ) = 1/ 2・K C2 cos2 (ωt + φ)
で与えられ,位置エネルギー U(x) は,
U(x) = 1/ 2・K C2 sin2 (ωt + φ)
で与えられ,全エネルギー E は,
E = K(x) + U(x) = 1/ 2・K C2 ( cos2 (ωt + φ)+sin2 (ωt + φ) )
ピタゴラスの定理より
E = 1/ 2・K C2
となり,力学的エネルギー保存の法則が成立する。
【参考:基礎用語】
- 調和振動子(harmonic oscillator)
振子のように振動する物体のうち,とくに質点が定点からの距離に比例する力を受けて運動する力学系をいう。
ページの先頭へ
【単振動の合成】
2 つ以上の波が同一の点を通過すると,“各々の波による変位を加え合わせたものが実質部分の結局の変位となる”が波の重ね合わせの原理(principle of superposition)といわれている。重ね合わせの原理は,重畳(ちょうじょう)原理ともいわれる。
同じ周期・同じ方向に進む単振動の合成
振動の方向が同じ 2 つの単振動では,振幅 C と初期位相 δが異なり,周波数すなわち角速度ωが同じ波の合成となる。この時,波 1 の変位 x1 と波 2 の変位 x2 は,
x1 = C1 sin (ωt + δ1 ) , x2 = C2 sin (ωt + δ2 )
で表される。これの合成された波の変位 x は,三角関数の加法定理を用いた展開で,
x = x1 + x2 = ( C1 cosδ1 + C2 cosδ2 ) sinωt + ( C1 sinδ1 + C2 sinδ2 ) cosωt
となる。
ここで,
C cosδ= C1 cosδ1 + C2 cosδ2
C sinδ= C1 sinδ1 + C2 sinδ2
となる振幅 C ,初期位相δ を求めると,
X = C sin (ωt + δ )
が求める合成正弦波となる。
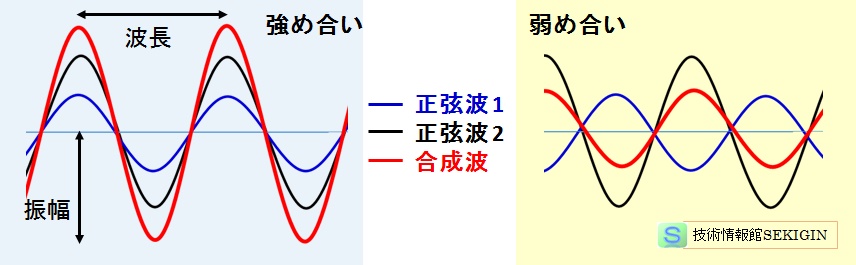
同じ周期の単振動の合成
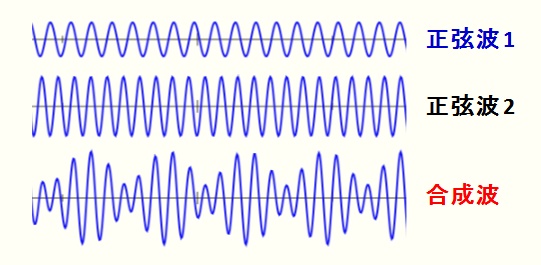
周期・振幅の異なる単振動の合成例
- 加法定理(addition theorem)
関数 f(α+β)=F{f(α) , f(β)}の関係で表される定理。三角関数,指数関数,ベッセル関数,楕円関数などの加法定理がある。
三角関数の加法定理
sin(α±β) = sinαcosβ± cosαsinβ
cos(α±β) = cosαcosβ ∓ sinαsinβ
tan(α±β) = (tanα±tanβ)/ (1∓ tanαstanβ) - 角速度(angular velocity)
平面上を運動する点と原点を結ぶ線分(動径)が,原点を通る基線(定めた直線)となす角が,時間的に変化する割合(速さの程度)をいう。
角速度は,原点を通り平面に垂直で,基線からこの動径の方向へまわした右ねじの進む向きのベクトルで表される。
ページの先頭へ
【減衰振動】
前述の単振動は,空気抵抗や摩擦などの外力を無視した理想状態で,実際には質点に抗力が働き振動はしだいに減衰する。
このような運動を減衰振動(damped vibration)と呼ぶ。抗力が質点の速度に比例する場合には,振幅が指数関数的に減少する。
なお,電気振動においても,減衰振動が起こる電気回路( RLC 回路など)がある。
ここで,減衰振動について,下図に示すばね振り子を例に考える。
ばね振り子では,一端が固定され,ばねとダッシュポットの並列する装置の他端に結合された質量 m の物体が,外力とし加振力(excitation force)を受けて振動している。
ある位置 x の物質には,ばねのフックの法則による復元力(restoring force),及びダッシュポットの抵抗による減衰力(damping force),運動する物質の慣性力(inertia)が作用する。
復元力 fr
フックの法則に従いばね定数 k のばねの復元力は,慣性力と反対の方向を向くので,次式で与えられる。
![]()
減衰力 fD
減衰係数 C のダッシュポットの場合には,ピストンの運動速度に比例するので, 次式で与えられる。
![]()
慣性力 fi
質量×加速度で与えられるが,復元力,減衰力と反対の方向を向く。
![]()
物質の振動において,力のつり合いは,
pt + fi = fr + fD
で表されるので,加振力 ptでまとめると,
![]()
と書ける。
これは,1 質点系の振動方程式(equation of vibration)といわれている。
ここで,これは減衰強制振動を表し,外力(加振力 pt )を取り去った後の振動方程式,すなわち右辺を 0 とした微分方程式の解を求めることで,減衰自由振動の挙動が説明される。
減衰自由振動方程式
単振動の節で紹介したように,抗力のない場合の角振動数ω0( rad/ s )は,質点の質量 m ,ばね定数 k(Nm‐1)を用いて,
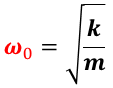
の関係で表される。減衰振動では,この角振動数ω0( rad/ s )を固有振動数という。
ここで,前述の1 質点系の振動方程式の両辺を質量 m で割り,
![]()
に置き換えると,振動方程式は,
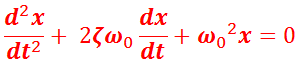
となる。ここで,CC を臨界(粘性)減衰係数(critical viscous damping constant),ζ (ゼータ)を減衰比(damping ratio)という。
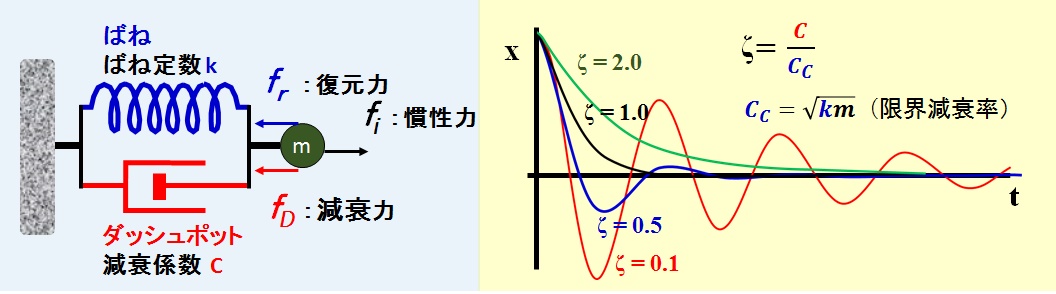
減衰振動の例
- 振動方程式(equation of vibration)
微小振動や電磁振動などの振動現象のモデルを扱う式をいう。 - 強制振動(forced vibration)
時間とともに振動的に変化する外力が働くと,最初の過渡的な振動の減衰の後に,質点は外力と同じ振動数で振動することをいう。
共鳴,共振は,外力の振動数が質点の固有振動数に等しいときにおきる。 - ダッシュポット(dash pot)
シリンダ内に流体とピストン部を封入し,ピストンの運動速度に比例した抵抗を得るようにした機械要素で,機械構造や建築物の振動を減衰するショックアブソーバー(Shock absorber)やダンパー(damper)などと呼ばれる装置の一種である。 - フーリエ変換(Fourier transform ,略号 FT )
フーリエ分解ともいい,与えられた関数を別の周期関数に分解して表現する際に用いられる数学的手法で,ある信号に含まれる周波数成分の解析,通信・画像処理などの実用分野で広く利用される。
ページの先頭へ
【減衰振動方程式の解】
この運動の解は,初期の振幅 x0 ,初期速度σとした時,減衰比 ζの値の範囲により,次の 4 種が得られる。
ζ= 0(不減衰振動=単振動),ζ= 1(臨界減衰:critical damping),1 < ζ(過減衰:over damping)となり,減衰振動は,0 < ζ < 1の場合である。
末岡淳男,金光陽一,近藤孝広著「機械振動学」(朝倉書店)では,減衰振動の解を
![]()
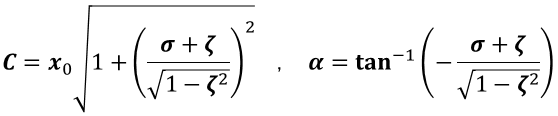
と記してる。
この系の角振動数
![]()
は,減衰が無い場合よりも小さくなり,減衰固有角振動数(damped natural angular frequency)という。
ページの先頭へ