物理 第二部:古典力学の基礎
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,力学的運動に関連し, 【運動量・力積の関係】, 【運動量保存の法則】, 【 2つの物体の衝突と反発】, 【物体の合体と分裂】, 【力学的エネルギー保存の法則と運動量保存の法則】 に項目を分けて紹介する。
【運動量・力積の関係】
運動量(momentum)とは,物体の運動の激しさを示すベクトル量(運動方向を含む)で,複数の物体の全運動量はベクトル和で表される。(ここでは,ベクトルを太字で表す。)
すなわち,質量 m の質点が速度 ν で運動している場合は,その積を運動量といい,ベクトル量 p = mν になる。なお,運動量の単位は,kg・m・s‐1 である。
円運動などでの角運動量と区別する場合は,線運動量ともいう。
運動量の式から分かるように,運動量は,同じ速度なら質量に比例し,同じ質量なら速度に比例する。なお,速度の二乗に比例する運動エネルギー ![]() とは異なる概念の量である。
とは異なる概念の量である。
運動量の時間的変化の割合は,
⊿p/ ⊿t = m・⊿ν/ ⊿t = ma = F
と,ニュートンの運動方程式の物体に働く力 F に等しい。
また,ある時間の間( t0 → t1 )で変化した運動量⊿p( = p(t1) – p(t0) )は,運動量の時間的変化の割合を時間帯で積分した量で,
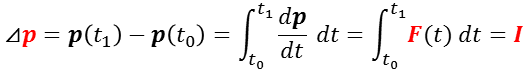
となり,力を時間で積分した量 I(力積)に等しい。
力積(impulse)とは,力 F が働く時間⊿ t との積(積分)で与えられるベクトル量 I = F・⊿ t (単位:N・s )をいい,時間内に力を受ける物体の運動量に等しく,打撃や衝撃などの物体間の接触で作用する短時間の大きな力(撃力:impulsive force )の評価などに用いられる。
質量 m の物体が,⊿t 時間の間に,速度νからν’に変化した時,その物体が受けた力積 I と物体に働いた力 F には,
I = m・ν - m・ν’ = ⊿p
F = I/⊿t
の関係にある。
これらは,ベクトルの合成・分解が可能なので,物体が複数の力を受けた場合は,それぞれの力積の和として考えることができる。
【参考:基礎用語】
- 撃力(impulsive force )
衝突や打撃などのきわめて短時間だけ作用する力をいう。撃力では,力もそれが作用している時間も測れないので,物体の運動の状態変化から(力×働いた時間)のベクトル量(力積)を直接求めて表す。 - 力学系(dynamical sysytem)
力学系とは,天体力学の研究から発生した概念で,与えられた集合上の点が時間とともに推移していく状況を数学的に記述する一つの方法である。 - デカルト(René Descartes)
ルネ・デカルト(1596年~1650年),フランス生まれの哲学者,数学者。哲学史上でもっとも有名な命題「我思う,ゆえに我あり」で知られ,「合理主義哲学の祖」,「近世哲学の祖」といわれ,「運動量保存の法則」の概念の提唱者でもある。 - ホイヘンス(Christiaan Huygens)
ホイヘンスの原理で知られるクリスティアーン・ホイヘンス(1629年~1695年),オランダの数学者,物理学者,天文学者,1690年に光の波動説を提唱する『Traite de la lumiere:光についての論考』を発刊。 - モーメント(moment)
ベクトルで表される物理量とある原点に対する位置の外積をいう。 - 弾性衝突(elastic collision)
一般に,2 つの弾性体の衝突をいう。反発係数 e の値に応じて,完全弾性衝突( e=1 ),塑性衝突又は完全非弾性衝突( e=0 ),非弾性衝突( 1>e>0 )と区分して呼ばれることがある。 - 弾性体(elastic body)
力を加えていると変形するが,力を除くともとに戻る物体をいう。フックの法則に従う弾性体を線形弾性体又はフック弾性体という。
ページの先頭へ
【運動量保存の法則】
運動量保存の法則(law of conservation of momentum)とは,“ある力学系に外力が存在しない場合,あるいは力のモーメントがゼロである場合には,この系の運動量の総和は常に一定で変化しない。”という基本的な物理法則の一つである。
フランスの哲学者,数学者であるデカルト(1596年~1650年)が提唱し,オランダの数学者,物理学者,天文学者のホイヘンス(1629年~1695年)により完成されたといわれる法則である。
運動量保存の法則の特徴
・ 力学系の運動量の総和が変わらない。
・ 力学系の重心は直線運動する。
運動量で紹介したように,物体に力が働いた時に,物体の運動量が変化する。この時,物体に働く力には,【主な力の概要】で紹介したように,対象とする力学系の外から働く力(外力という)場合と力学系の内部で働く力(内力という)に分けられる。
例えば,2 つの物体が衝突した時,その瞬間に,両物体には作用・反作用の法則に従い,互いに同じ大きさで反対方向の力,すなわちベクトル和がゼロとなる内力が作用する。
多段式ロケットの切り離しや核分裂のように,1 つの物体が分裂する時にも,作用・反作用の法則に従い,分裂した複数の物体に作用する力のベクトル和がゼロとなる内力が作用する。
このような,外力の作用しない状況での衝突や分裂では,運動量が保存される。
衝突・分裂の例
物体の衝突,分裂で,一般的に見られる主な現象には次の物がある。
・ 2 つの物体の衝突後に跳ね返り,衝突前とは異なる方向と運動量で運動する場合。
・ 逆に,2 つの物体の衝突後に密着(接着,連結など)し,あたかも 1 つの物体として振る舞う場合。
・ 1 つの物体が内部に発生した力で 2 つ以上の物体に分裂して運動する場合。
ページの先頭へ
【 2 つの物体の衝突と反発】
衝突後の反発
外力の作用しない状態で,等速直線運動する物体 A(質量 mA ,速度νA )と物体 B(質量 mB ,速度νB )で構成される系を考える。
物体の衝突では,図に例示するように,衝突した 2 つの物体が跳ね返り,運動方向と速度が変わる。
衝突の瞬間に,両物体には作用・反作用の法則に従い,互いに同じ大きさで反対方向の力(内力 F )が極短い時間(⊿ t 秒)作用する。すなわち,物体 A は物体 B に力積 F・⊿t を及ぼし,物体 B は物体 A に力積‐F・⊿t を及ぼす。
前述したように,力積は運動量の変化量に相当する。すなわち,衝突後の速度を物体 A(速度νA’ )と物体 B(速度νB’ )とすると,
衝突後の物体 A の運動量変化と力積の関係,
mA・νA’ ‐mA・νA =‐F・⊿t
物体 B の運動量変化と力積の関係,
mB・νB’ ‐mB・νB = F・⊿t
となる。
そこで,両式を力積の F・⊿t でまとめると,
mA・νA + mB・νB =mA・νA’ + mB・νB’
となる。
すなわち,衝突時の力積の大きさによらず,運動量保存の法則が成り立つことが分かる。
衝突とは
物理現象の衝突(collision)とは,運動している2つの物体が接触し,ごく短時間に撃力を相互に及ぼし合う現象をいう。
物体の衝突後に,跳ね返る現象は,比較的頻繁に経験される現象である。物体の種類により跳ね返りの程度の違いも良く経験される。
この跳ね返りの程度の違いは,衝突前後の接触面の法線方向の相対速度の比となる反発係数(coefficient of restitution)で評価される。
単純化して,外力の働かない状況で,同一直線上を等速直線運動する 2 つの物体(球体)の衝突で例示する。この場合は,衝突の接触面の法線方向は,物体の運動方向と同一の方向となる。
物体 A(質量 mA ,速度νA )が物体 B(質量 mB ,速度νB )を追いかけて衝突(νA >νB )し,物体 A の速度がμA ,物体 B の速度がμB に変化した。
反発係数 e は,衝突前後の接触面の法線法の相対速度の比で与えられるので,
e = ‐(μA‐μB )/ (νA ‐νB )
となり,0 ≦ e ≦ 1 の値をとる。
一般的には,e=1 のときを完全弾性衝突,e=0 のときを完全非弾性衝突,1>e>0 のときを非弾性衝突というが,単に弾性衝突(elastic collision)という場合は,完全弾性衝突を指す場合が多い。
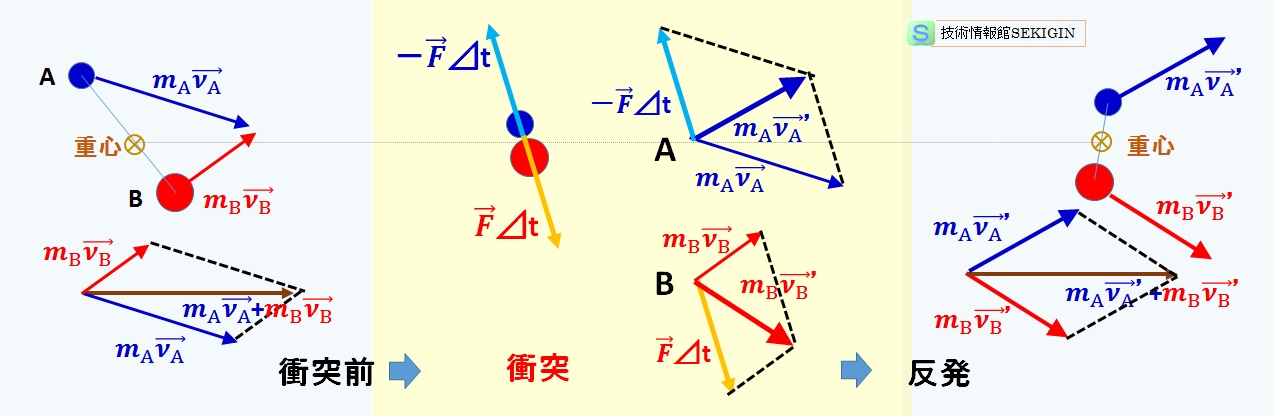
物体の衝突・跳ね返りの例
ページの先頭へ
【物体の合体と分裂】
衝突後一つの物体として運動
衝突後に一つの物体として運動するのは,前出の「衝突と反発」の例での反発係数 e = 0(完全非弾性衝突)の場合である。
運動量保存の法則により,衝突前の 2 つの物体の運動量と衝突後の運動量が保存されるので,一つに合体した後の速度νとすると,
mA・νA + mB・νB = ( mA + mB )・ν
∴ ν= ( mA・νA + mB・νB )/ ( mA + mB )
となる,質量 m(= mA + mB )の合体した物質は,合体前の 2 つの物体のベクトル合成,すなわち重心の運動方向に速度νで移動する。
物体の分裂
外力の作用しない状態で,等速直線運動する物体(質量 m ,速度ν )の内部で力が発生し,物体 A(質量 mA ,速度νA )と物体 B(質量 mB ,速度νB )に分裂した場合を考える。
物質内部では,分裂後の物体の界面に相当する位置で,作用・反作用の法則に従い,互いに同じ大きさで反対方向の力(内力 F )が極短い時間(⊿ t 秒)作用する。
これにより,分裂した物体 A は物体 B に力積 F・⊿t を及ぼし,物体 B は物体 A に力積‐F・⊿t を及ぼす関係になる。
これは,前出の「衝突と反発」の例での衝突時と同様の関係と考えられるので,分裂前の物体の速度νと力積とのベクトル和に従って,それぞれの物質の運動量が得られる。
しかしながら,内力の大きさと方向が不明なため,実質的にはベクトル和を求められない。そこで,分裂前の物体の運動方向に対する分裂後の物質 A の運動方向との成す角(θA ),及び物質 B の運動方向との成す角(θB ),分裂後の質量( mA ,mB )が分かれば,運動量保存の法則から,
mν= mAνA cosθA + mBνB cosθB
0 = mAνA sinθA - mBνB sinθB
の関係がえられる。
これにより,分裂後の速度のスカラー値(νA,νB )を求めることができる。
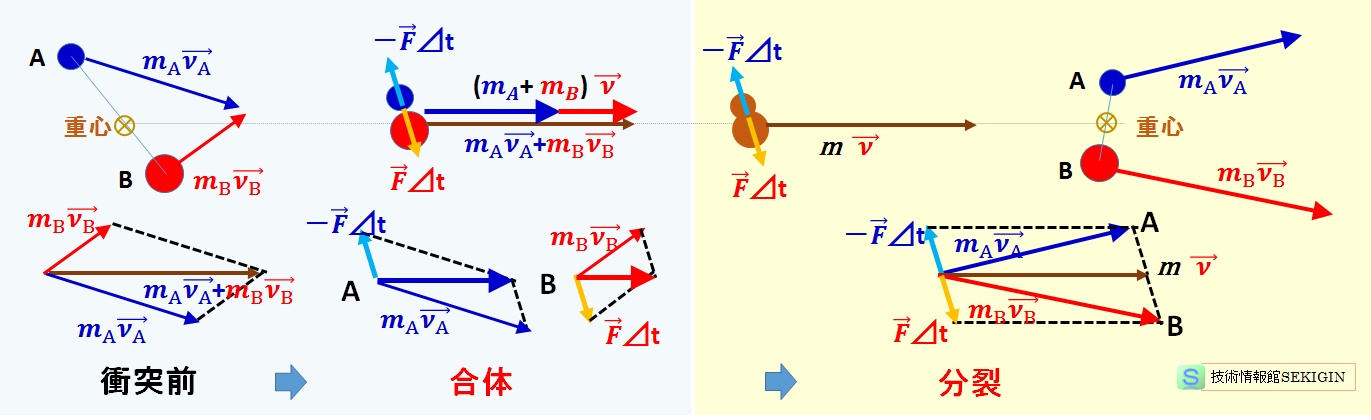
物体の合体と分裂の例
ページの先頭へ
【力学的エネルギー保存の法則と運動量保存の法則】
力学的エネルギー保存の法則とは
物体の持つ運動エネルギーと位置エネルギーの和を指す力学的エネルギーは,保存力のみが作用する保存力場(conservative force field)で一定となる力学的エネルギー保存の法則(law of the conservation of mechanical energy)が成立する。
すなわち,運動エネルギー K ,位置エネルギーU のとき,力学的エネルギー E は,
K + U = E(一定)
で表される。
ここで,重力場で,地表と水平に高さ h 一定で等速直線運動する物体(質量 m ,速度ν)の運動エネルギー K は,
![]()
となり,物体の高さ h での位置エネルギー U は,重力加速度 g とすると,
U = mg h =一定
で与えられる。
物体衝突前後の力学的エネルギー
単純化して,外力の働かない状況で,地表と水平に高さ h 一定で,同一直線上を等速直線運動する 2 つの物体(球体)の衝突を考える。
物体 A(質量 mA ,速度νA )が物体 B(質量 mB ,速度νB )を追いかけて衝突(νA >νB )し,物体 A の速度が μA ,物体 B の速度がμB に変化した。
一方,衝突前後の運動量保存の法則より,
mAμA+mAμB = mAνA+mBνB
このとき,反発係数 e は,
e = ‐(μA‐μB )/ (νA ‐νB )
∴ μA‐μB =‐e (νA ‐νB )
で与えられる。
これらより,衝突後の速度μAは,
mAμA+mB{μA+ e (νA ‐νB)}= mAνA+mBνB
∴μA=[(mA‐mB e )νA+mBνB ( 1 + e )] /(mA+mB )
=νA‐(νA ‐νB )[( 1+e )mB / (mA+mB )]
同様にして,衝突後の速度μBは,
μB=[( 1+e )mAνA +( mB‐mA e )νB)] /(mA+mB )
=νB+(νA ‐νB )[( 1+e )mA / (mA+mB )]
となる。
重力場での高さ一定,一直線上での衝突なので,位置エネルギー U は不変であるが,物体の速度が変化している。そこで,衝突前後の運動エネルギー K ( (1/2)・mν2 )の差⊿K を求めると,
⊿K = (1/2)・mA(νA2‐μA2 )+1/2・mB(νB2‐μB2 )
=(1/2)・(νA ‐νB ) 2 ・ [ mA・mB/ (mA+mB)] ・ ( 1‐e2 )
が得られる。
すなわち,反発係数 e=1 (完全弾性衝突)では⊿K= 0 となり,運動エネルギーも不変で力学的エネルギー保存の法則が成立する。
しかし,その他の場合( e>0 )は,力学的エネルギー保存の法則は成立せず,運動エネルギーが減少する。一般的には,運動エネルギー変化に相当するエネルギーは熱などの他のエネルギー形態に変換される。
ページの先頭へ