物理 第一部:物理学とは
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,運動の表し方に関連し,【速さと速度】,【変位と速度】,【加速度】に項目を分けて紹介する。
【速さと速度】
日常生活では,速さと速度を区別して用いることは少ないが,物理学では,速さ(speed)と速度(velocity)は厳密に区別される。
速さ(speed)
物理学の速さは,各時刻の位置が特定でき,時間とともに移動する場合,移動距離の時間的な変化率を表す量である。
移動距離を X ,移動に要した時間を t とした場合に,速さ V は次式で与えられる。
V = x/t
速さは,移動の方向を問わない単位 m/s :メートル毎秒(又は m/h :メートル毎時)の正の値を持つスカラー量である。この結果は,言い換えれば,移動した区間(又は時間帯)における平均の速さとなる。また,一定速度で移動した場合は,単位時間あたりの移動距離となる。
速度(velocity)
物理学の速度とは,運動している質点の単位時間あたりの方向を含む変位を表すベクトル量である。
一般的には,運動している質点のある瞬間において,極めて短い時間⊿ t の間に移動した距離 ⊿ x とした場合に,速度のスカラー量 |![]() |は次式で与えられる。
|は次式で与えられる。
|![]() |= ⊿ x /⊿ t
|= ⊿ x /⊿ t
速度は方向を持つため,スカラー量は正負の符合を持つ,定めた条件下の速さ(平均の速さ)で表す場合は,速度の絶対値が用いられる。
速度を厳密に定義すると,一般的には加速度の影響を受けるので,距離の時間に対する変化率は一定とは限らない。そこで,位置 x の時刻 t に対する変化を表すグラフを考え,ある時刻の勾配が速度![]() と定義できる。すなわち,x を tで微分した量になる。
と定義できる。すなわち,x を tで微分した量になる。
![]() = dx/ dt
= dx/ dt
ある時刻の速度の絶対値は,瞬間の速さともいわれる。
【参考:基礎用語】
- スカラー量(scalar quantity)
長さ・面積・質量・温度・時間などの大きさだけで定まる数量。 - ベクトル(vector)
大きさに加え,方向と向きをもつ量で,変位,力,速度,電場,磁場などが例として挙げられる。物理学では,これらの他にもベクトルとして示される量は少なくない。 - 位置ベクトル(position vector)
平面または空間のある点を O と定め、任意の点を A とするとき,O を始点とし A を終点とするベクトルをいう。すなわち,位置ベクトルは,基点 O に対する A の距離と方向とを示す。 - 変位(displacement)
物体が運動して位置が変わった時,位置の変化量をいう。この場合,物体の移動経路(軌跡)は問われず,最初と最後の位置のみを問題とする。 - 接線(tangent line)
接線とは,曲線上の一点が与えられたとき,その点で曲線に「ただ触れるだけ」の直線をいう。 - 法線(normal)
曲線では,ある点接線に垂直な直線を,曲面では,ある点の接平面に垂直な直線を,その点の法線という。
ページの先頭へ
【変位と速度】
変位(displacement)
物体が運動して位置が変わった時,位置の変化量を変位という。この場合,物体の移動経路(軌跡)は問われず,最初と最後の位置のみを問題とする。
物体が位置 A から位置 B へ動く変位は,AB 間の距離と方向を持つので,![]() とベクトルで表わされる。
とベクトルで表わされる。
基準となる地点( O )から位置 A ,B の位置ベクトル![]() ,
,![]() で与えられれば,変位ベクトルは,下図に示すように,和ベクトル(合成ベクトル)を用いて,
で与えられれば,変位ベクトルは,下図に示すように,和ベクトル(合成ベクトル)を用いて,
![]() =
=![]() ‐
‐ ![]()
で表わされる。
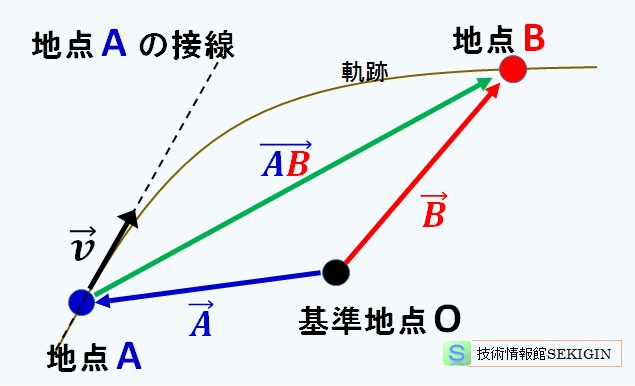
変位ベクトル
速度(velocity)
地点 A から地点 B に移動するまでに要した時間を t とすると,物体の速度(平均の速度)
となる。観測時間 t を限りなく短くすると,地点 A における瞬間の速度となり,その方向は,数学における微分法(differential calculus)でおなじみの軌跡の接線の方向に等しくなる。
すなわち,物体移動の軌跡を位置と時間の関数で表すことができれば,任意の地点における瞬間の速度を数学的に求められることを示す。
速度の合成と分解
以上で示したように,速度はベクトル量であるので,平行四辺形の法則に従い,ベクトルの合成,ヘクトルの分解が可能である。
例えば,風船が空気との密度差で上昇するとともに,風の影響を受けて流される場合の風船の速度ベクトルは,風船の上昇の速度ベクトルと風の速度ベクトルに分解できる。なお,分解された 2 つの速度を分速度ともいう。
同様にして,三角関数(sinθ ,cosθ)を用いることで,斜めに移動する物体の速度を,二次元の運動では X 成分と Y 成分に,三次元の運動では,X 成分,Y 成分と Z 成分に分解し,説明を容易にすることもできる。
以上は,一つの物体の運動についてであるが,二つの物体の運動のベクトル合成で相対速度などの相対的な運動の説明も可能になる。
ページの先頭へ
【加速度】
加速度(acceleration)とは,単位時間当たりの速度の変化率をいう。なお,速度![]() はベクトル量のため,加速度
はベクトル量のため,加速度![]() もベクトル量になる。
もベクトル量になる。
![]() =
=![]() /⊿ t
/⊿ t
すなわち,速度の単位は(m/s =ms‐1)なので,加速度の単位は,m/s2(=ms‐2:メートル毎秒毎秒)となる。また,速度と同様に,時間間隔の与え方で平均の加速度と瞬間の加速度に分けられる。
位置ベクトルが時間の関数として与えられた場合には,(瞬間の)速度は位置ベクトルを時間で微分することで求められ,(瞬間の)速度を時間で微分すると(瞬間の)加速度が求められる。
加速度もベクトルの平行四辺形の法則で合成,分解ができる。曲線運動する場合は,加速度を接線加速度,法線加速度に分解することが多い。(瞬間の)速度は常に軌跡の接線方向を向くので接線加速度は速さの変化を表し,接線と鉛直方向に分解された法線加速度は運動の向きの変化を表わす。
ページの先頭へ