物理 第六部:電磁気学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,電気回路に関連する基本法則として, 【基本法則について】, 【オームの法則】, 【キルヒホッフの法則】, 【ビオ・サバールの法則・アンペールの法則】 に項目を分けて紹介する。
【基本法則について】
電磁気学を理解するうえで必要な基本法則として,フレミングの右手・左手の法則,右手の法則(右ねじの法則),ファラデーの法則,電磁誘導の法則,クーロンの法則,ガウスの法則,ジュールの法則,マクスウエルの方程式,シュテファン・ボルツマン則,オームの法則,キルヒホッフの法則,ビオ・サバールの法則,アンペールの法則などが挙げられる,
この中で,黒字で示したフレミングの法則(右手の法則,左手の法則),右手の法則(右ねじの法則),ファラデーの法則,電磁誘導の法則は,【電流と磁場】で紹介した。
クーロンの法則は,【電荷と帯電】で紹介し,ガウスの法則は,【電場】で紹介した。
ジュールの法則は,【仕事とエネルギー】で紹介した。
マクスウェルの方程式は,【電磁波とは】で,シュテファン・ボルツマン則は,【放射熱】で紹介した。
ここでは,赤字で示したオームの法則,キルヒホッフの法則,ビオ・サバールの法則,アンペールの法則を紹介する。
【電気工学の発展に寄与した主な研究者】
- フレミング(Sir John Ambrose Fleming)
ジョン・アンブローズ・フレミング(1849年 ~ 1945年)は,イギリスの物理学者,電気技術者で,真空管の発明,フレミングの法則の考案で知られる。 - ファラデー(Michael Faraday)
マイケル・ファラデー(1791年~1867年)は,イギリスの化学者,物理学者で,ファラデーの電磁誘導の法則,ファラデーの電気分解の法則,ファラデー定数など電磁気学,電気化学への貢献で知られる。 - クーロン(Charles-Augustin de Coulomb)
シャルル=オーギュスタン・ド・クーロン(1736年 ~ 1806年)は,フランスの物理学者で,帯電した物体間に働く力を測定からクーロンの法則を発見した。業績に因んで,電荷の単位に「クーロン; C 」が用いられている。 - ガウス(Carolus Fridericus Gauss)
カール・フリードリヒ・ガウス(1777年 ~ 1855年)は,ドイツの数学者,物理学者で,近代数学,電磁気学など物理学に多くの業績を残す。 - ジュール(James Prescott Joule)
ジェームズ・プレスコット・ジュール(1818 年~1889 年)は,イギリスの物理学者。ジュールの法則の発見,熱の仕事当量,マイヤー,ヘルムホルツと共にエネルギー保存則(熱力学第一法則)の発見者,など熱力学の発展に寄与し,単位ジュール( J )として名をとどめる。 - マクスウェル(James Clerk Maxwell)
ジェームズ・クラーク・マクスウェル(1831年~1879年)は,イギリスの理論物理学者。熱力学のマクスウェルの関係式,電磁気学のマクスウェルの方程式,統計力学のマクスウェル分布(マクスウェル・ボルツマン分布)で知られる。 - シュテファン(Joseph Stefan)
ヨーゼフ・シュテファン(1835年 ~ 1893年)は,オーストリアの物理学者,数学者で,シュテファン=ボルツマンの法則で知られるボルツマンの師である。 - ボルツマン(Ludwig Eduard Boltzmann)
ルートヴィッヒ・エードゥアルト・ボルツマン(1844年~1906年)は,オーストリア・ウィーン出身の物理学者,哲学者。統計力学,電磁気学,熱力学,ボルツマンの関係式,ボルツマン定数などで知られる。 - オーム(Georg Simon Ohm)
ゲオルク・ジーモン・オーム(1789年 ~ 1854年)は,ドイツの物理学者で,電位差と電流に関するオームの法則を発見し,電圧,電流,電気抵抗の基本的な関係の定義による電気回路解析分野の創始者として知られる。 - キルヒホフ(Gustav Robert Kirchhoff)
グスタフ・ロベルト・キルヒホフ(1824年 ~ 1887年)は,プロイセン生まれのドイツの物理学者で,キルヒホッフの法則(電気回路,放射エネルギー,化学反応熱),分光学,音響学で知られる。 - ビオ(Jean-Baptiste Biot)
ジャン=バティスト・ビオ(1774年 ~ 1862年)は,フランスの物理学者,天文学者で,電流と磁場の関係の研究成果は,サバールと共にビオ・サバールの法則の発見者として知られる。また,偏光の研究等でも知られる。 - サバール(Félix Savart)
フェリックス・サヴァール(1791年 ~ 1841年)は,フランスの物理学者,医師で,ジャン=バディスト・ビオと共同の電流と磁場に関するビオ・サバールの法則の発見者として知られる。 - アンペール(André-Marie Ampère)
アンドレ=マリ・アンペール(1775年 ~ 1836年)は,フランスの物理学者,数学者で,アンペールの法則の発見など電磁気学の創始者の一人とされる。なお,電流のSI基本単位「A:アンペア」はアンペールの名に因んで命名されている。 - キャヴェンディッシュ(Henry Cavendish)
ヘンリー・キャヴェンディッシュ(1731年 ~ 1810年)は,イギリスの化学者,物理学者で,金属と強酸の反応により水素が発生すること,電気火花を使った水素と酸素の反応により水が生成すること,すなわち水が水素と酸素の化合物であることを発見したことで知られる。
物理分野では,未公開のため,彼の業績とはされていないが,気体の蒸気圧や熱膨張に関する発見,クーロンの法則,オームの法則に匹敵する発見など多くの研究を行っている。 - オーム,ジーメンスの単位換算
S = Ω–1 = A・V–1 = C2・s・kg–1・m–2 = A2・s3・kg–1・m–2
ページの先頭へ
【オームの法則】
オームの法則(Ohm's law)は,導電現象において,電気回路の部分に流れる電流 I とその両端の電位差 V の関係を示す最も基本的な法則として有名である。
この法則は,イギリスの化学者,物理学者キャヴェンディッシュがすでに発見していたが,公表していなかったため,マクスウェルが『ヘンリー・キャヴェンディシュ電気学論文集』として出版されるまでこの法則の発見者として認められていなかった。
一方,マクスウェルの出版前に,ドイツの物理学者オームが独自に発見・公表していたため,この法則は,オームの法則と名付けられた。
オームの法則では,電気回路の 2 点間の電位差 V が 2 点間に電流 I に比例する。すなわち,
V = R I
の関係がある。R は,2 点間の導線とその状態によって決まる定数で,2 点間の電気抵抗(electric resistance)といい,SI 組立単位としてオーム( ohm ,記号Ω)を用いる。
上式の関係は,
I = G V
とも書くことができ,G は R の逆数で,電気伝導度(コンダクタンス,conductance)といい,単位として,古くはモー(mho ,記号 ℧)を用いていたが,現在の SI 組立単位ではジーメンス(siemens ,記号 S )が用いられる。
導体内の微小領域におけるオームの法則として,電場 E( V・m–1 )と電流密度 j( A・m–2 )で,
E =ρ j
j =σ E
と表される。
ρ は電気抵抗率(electrical resistivity),抵抗率(resistivity),比抵抗(specific electrical resistance),固有抵抗(specific resistance)とも呼ばれ,電気の通し難さの比較で用いられる物性値で,単位はオームメートル(Ω・m)である。
σは電気伝導率(electrical conductivity),導電率(conductivity)ともいい,電気伝導のし易さを表す物性値で,単位は ジーメンス毎メートル (S・m–1),又は毎オーム毎メートル(Ω–1・m–1)である。
ページの先頭へ
【キルヒホッフの法則】
キルヒホッフの法則(Kirchhoff's law)とは,ドイツの物理学者キルヒホフが発見した法則に対する一般的な呼称であるが,技術分野の異なる次の 3 つの法則をいう。
● 電気分野の電気回路の電流と電圧に関するキルヒホッフの法則(電気回路)
● 電磁波分野の黒体放射など局所熱平衡状態で成り立つ,光と物体の相互作用に関するキルヒホッフの法則(放射エネルギー)
● 熱化学分野の反応熱の温度係数が反応前後の熱容量の差に等しいというキルヒホッフの法則(反応熱)
ここでは,電気回路に関するキルヒホッフの法則を紹介する。
一般的な電気回路は,電源,抵抗などの複数の部品を結ぶ複雑な構造を持つ。この回路を流れる電流は,キルヒホッフの法則(電気回路)の第一法則と第二法則で表した連立方程式の解として求めることができる。
なお,交流電流にも適用できるので,コイル(インダクタ)やコンデンサを含めて抵抗成分をインピーダンス(impedance)に読み替えて計算されるのが一般的である。
第一法則(電流則)
電気回路の任意の接続点において,流入する電流と流出する電流の和は等しい。
第二法則(電圧則)
電気回路の任意の接続点から出発してふたたび初めの接続点に戻る閉じた径路(閉路)において,電圧の向きを一方向に取ったとき,電圧の総和は 0 となる。
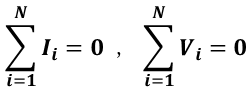
ページの先頭へ
【ビオ・サバールの法則・アンペールの法則】
ビオ・サバールの法則(Biot-Savart law)
フランスの物理学者ビオとサヴァールが発見した電流の存在によってその周りに生じる磁場を求める法則である。
磁場は距離,方向,および電流の大きさなどに依存すること示し,静的な近似ではアンペールの法則および磁場に対するガウスの法則と同等のものである。
【電流と磁場】では,磁場は電流の流れている電線を取り囲む同心円状の線で表され,電流の方向と磁場の方向は右手の法則(右ねじの法則)に従うことを紹介した。
同時に,直線導線に電流を流したときに,導線 A の電流 iA の作る磁束密度 B の中に置かれた電流素片 i dS が受けるアンペールの力が,
![]()
で,電流 iA の導線からの距離 r の位置の磁束密度の大きさは,
![]()
となることも紹介した。これは,ビオ・サバールの法則を積分した形と一致する。
ビオ・サバールの法則では,任意の形をした導線を流れる電流 i によって生じる任意の点 P の磁束密度 dB を知るには,電流素片 i dS に基づく磁束密度を知ればよいと考える。
すなわち,磁束密度 dB は,点 P と微小部分 dS とで作る三角形に垂直で,右手の法則(右ねじの法則)に従う方向を向くと考えられるので,dS から P までの距離を r ,idS と r の成す角をθとしたとき,
![]()
の関係が成り立ち,これをビオ・サバールの法則という。
アンペールの法則(Ampère's circuital law)
フランスの物理学者アンペールが発見した電流のまわりにできる磁場の関係をあらわす法則である。電流のSI単位アンペア(A)は,アンペールの業績にちなんで用いられている。
アンペールの法則は,上述の直線電流(定常電流 I )の周りの磁場の式を一般化した法則である。すなわち,閉じた経路(閉曲線 c )にそって磁場の大きさを足し合わせる(積分)することで求められる。距離 r の位置の磁束密度の単位ベクトル e B としたときの結果,
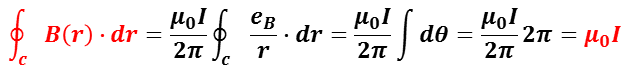
が得られる。
ページの先頭へ