物理 第二部:古典力学の基礎
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,力学的エネルギー保存に関し, 【エネルギー保存の法則とは】, 【力学的エネルギー保存の法則】, 【重力による運動:斜方投射】, 【重力による運動:振り子】, 【弾性力(フック力)による運動(単振動)】 に項目を分けて紹介する。
【エネルギー保存の法則とは】
エネルギー保存の法則(law of the conservation of energy)は,
“閉じた系(外界とエネルギーの出入りが無い系)において,エネルギーの移動,形態の変更などによっても,その総量が変化しない”
と定義され,物理学における保存則(conservation law)の一つで,短縮してエネルギー保存則ともいわれる。
19 世紀までに力学的エネルギー保存の法則(principle of mechanical energy)が確立され,その後に熱現象も含めた熱力学の第一法則(孤立系のエネルギーの総量は変化しない)がマイヤー,ジュール,ヘルムホルツらにより確立されたことで,音,光,電磁気,化学変化,原子核反応等を含めた自然現象を支配する基礎法則となった。
その後,相対性理論により,エネルギーと質量とは同等(質量とエネルギーの等価性: E = m c2 )であるとされ,エネルギー保存の法則と質量保存の法則が統一できるとも考えられているが,実用上ではそれぞれが成立している。
力学的エネルギー保存の法則とは,位置エネルギーの増減,運動エネルギーの増減を伴う変化においても,運動エネルギーと位置エネルギーの総和は変わらないことを示すが,前提として系に働く力が保存力のみの場合である。
保存力ではない摩擦力などの非保存力が作用している場合は,力学的エネルギー保存の法則は成立せず,摩擦力による仕事に相当するエネルギーが熱エネルギーに変換される。
熱的なエネルギーを含め,閉じた系(孤立系)におけるエネルギー保存の法則は熱力学第一法則(the first law of thermodynamics)と呼ばれる。
主要な保存則
エネルギー保存の法則以外に,基本的な保存則には運動量保存の法則(law of conservation of momentum),角運動量保存の法則(law of conservation of angular momentum)など物理的変化に対する保存則がある。化学的変化に対しては,さらに質量保存の法則(law of conservation of mass),電荷保存の法則(law of conservation of charge)などがある。
このように,考えている系内での変化前後で物理量の総和が変わらないという基本法則や保存則が成り立つ系のことを保存系(conservative system)と呼ぶ。
運動量保存の法則:運動量保存則ともいい,物体の衝突系など,ある系に外部からの力が加わらないかぎり,その系の運動量の総和は不変いう法則。
角運動量保存の法則:角運動量保存則ともいい,の略称単位時間あたりの全角運動量の変化は外力によるトルク(力のモーメント)に等しい(ただし内力が中心力であるときに限る)という法則。
質量保存の法則:質量保存則ともいい,素粒子論・核物理・宇宙論などを除く分野,特に化学で重要な法則,フランスの科学者アントワーヌ・ラヴォアジエが1774年に“化学反応の前と後で物質の総質量は変化しない”と提唱した。
電荷保存の法則:電荷保存則,電気量保存の法則などともいい,電荷の総量は永遠に変わらないという経験的に導かれた法則,すなわち,化学反応,原子核反応,粒子の崩壊など現在確認されている全ての反応で成立し,これに反する例が見つかっていないため経験的に導かれた法則といわれる。
【参考:基礎用語】
- マイヤー(Julius Robert von Mayer)
ユリウス・ロベルト・フォン・マイヤー(1814年~1878年),ドイツの物理学者。熱と仕事が相互に変換可能であること,エネルギー保存の法則を発表。比熱に関するマイヤーの関係式でも知られる。 - ジュール(James Prescott Joule)
ジェームズ・プレスコット・ジュール(1818 年~1889 年),イギリスの物理学者。ジュールの法則の発見,熱の仕事当量,マイヤー,ヘルムホルツと共にエネルギー保存則(熱力学第一法則)の発見者,など熱力学の発展に寄与し,単位ジュール( J )として名をとどめる。 - ヘルムホルツ(Hermann Ludwig Ferdinand von Helmholtz)
ヘルマン・ルートヴィヒ・フェルディナント・フォン・ヘルムホルツ(1821年~1894年),ドイツ出身の生理学者,物理学者。1847年に論文『力の保存について』を発表。マイヤー,ジュール,ケルビン卿と並ぶエネルギー保存則(熱力学の第一法則)確立者の一人。ヘルムホルツ方程式,ヘルムホルツの自由エネルギー,ケルビン・ヘルムホルツ不安定性,ギブズ-ヘルムホルツの式などで知られる。 - 三角関数
正弦関数(sine , sinθ),余弦関数(cosine , cosθ),正接関数(tangent , tanθ)には,tanθ = sinθ/ cosθの関係がある。 - 角度
単位は,原則としてラジアン(radian , 単位記号 rad )を用いる。ラジアンは「円周上でその円の半径と同じ長さの弧を切り取る 2 本の半径が成す角の値」(180°=πrad )と定義され,円弧の変位 S ,円弧の半径 l としたとき,角度θ(ラジアン,rad )は,S = l θ の関係にある。 - 三角関数の基本式
ピタゴラスの定理:sin2θ+ cos2θ = 1
対称性:sin( -θ) = - sinθ,cos( -θ) = cosθ,tan( -θ) = - tanθ
加法定理:sin(α±β) = sinαcosβ± cosαsinβ ,cos(α±β) = cosαcosβ ∓ sinαsinβ ,tan(α±β) = (tanα±tanβ)/ ( 1 ∓ tanαstanβ)
三角関数の合成:a sinθ+ b cosθ = ( a2 + b2 ) 1/2 sin ( θ+ φ) tan φ= sin φ/ cos φ= b/ a (a ≧ 0),b/ a +π(a< 0)又は,sin φ= b/ (a2 + b2 ) 1/ 2 ,cos φ= a/ (a2 + b2 ) 1/ 2
二乗:sin2θ = ( 1 – cos2θ)/ 2 ,cos2θ= ( 1 + cos2θ)/ 2
三角関数の微分:dsinθ/ dθ = cosθ , d2sinθ/ dθ2 = - sinθ dcosθ/ dθ= - sinθ, d2cosθ/ dθ2 = - cosθ
ページの先頭へ
【力学的エネルギー保存の法則】
力学的エネルギー(mechanical energy)とは,物体の持つ運動エネルギーと位置エネルギー(ポテンシャル)の和を指す。
保存力のみが作用する保存力場(conservative force field)で,質点の力学的エネルギーが一定となることを力学的エネルギー保存の法則(principle of mechanical energy)という。
すなわち,運動エネルギー K ,位置エネルギー U のとき,力学的エネルギー E は,
K + U = E(一定)
で表される。
運動エネルギー K の大きさは,ゼロ又は正の値をとるので,位置エネルギー U は,
U = E ‐ K ≦ E
となる。
すなわち,位置エネルギーは物体の初期状態で決まる総エネルギーを超えることができない(位置エネルギーが制限される)ので,運動の領域が決まることを意味する。
これは,地上で物体を投げ上げた時の放物線の頂点の存在,振り子やばねなどの周期的な運動の繰り返しの原理でもある。
なお,摩擦力や想定する系の外から与えられた力など,非保存力でした仕事がある場合は,系の力学的エネルギーは保存されず変化する。
ページの先頭へ
【重力による運動:斜方投射】
質量 m の物体の速度νの運動エネルギー K は,
![]()
で与えられる。
一方,物体の高さ h での位置エネルギー U は,重力加速度 g とから,
U = mgh
で与えられる。
力学的エネルギー保存の法則に従い,運動エネルギー K と位置エネルギー U の総和は,初期条件で決まる総エネルギーに一致する。
斜方投射
地表からの高さ h0 から初速度ν0,地平線との仰角θで斜方投射された質量 m の物体の持つ総エネルギー E は,
E = 1/2・mν02 + mgh0
で与えられる。
非保存力の摩擦が作用しないと仮定した場合は,物体に作用する力が保存力の重力のみなので,その後の物体の経路によらず運動エネルギーと位置エネルギーの和は保たれる。
従って,最高到達点を求めようとすると,地表面と平行な方向には力が作用していないので,物体の水平方向の速度(ν0cosθ)は変化しないので,物体の垂直方向の速度(ν0sinθ)がゼロとなる条件の高さ h を求めればよい。
すなわち,最高到達点(高さ h )での運動エネルギーは,水平方向のみの運動と考えられ, Kh = 1/2・m (ν0 cosθ)2 となる。
高さ h での位置エネルギーは,Uh = mgh となるので,最高到達点の高さ h での運動エネルギーと位置エネルギーの和と初期条件で決まるエネルギー E とから高さ h が求められる。
E = 1/2・mν02 + mgh0
= Kh + Uh = 1/2・m(ν0 cosθ)2 + mgh
ページの先頭へ
【重力による運動:振り子】
振り子(pendulum)とは,支点から吊るされた物体(おもり)が,重力の作用で揺れを繰り返す現象である。また,非保存力の支点での摩擦,空気抵抗などが無い環境では永久に揺れ続けられる。
ここで,非保存力が作用しない状態で,一端を固定(支点)された質量 0 ,長さ l の糸に質量 m のおもりをつるし,その後,おもりを半径 l の円周(弧)に沿って,支点から鉛直方向と成す角度θ0 (ラジアン,rad )まで移動させた後で,自由にした場合の運動を考える。
おもりに作用する力は,重力 mg であるが,この力はおもりの法線方向(円周の中心とおもりを結ぶ方向)と接線方向(円周の接線)に分けられる。
法線方向の力:mg cos θ0
接線方向の力:mg sin θ0
法線方向の力は,作用反作用により,おもりを支える糸の張力 T と釣り合う。張力 T は,おもりの位置で変化する値であるが,おもりを円周上に拘束する力として作用し,おもりの運動には作用しない。
一方,接線方向の力は,おもりの円弧に沿った運動の力になる。
おもりの持つエネルギー E は,手を離した位置(高さh )での位置エネルギーである。
E = mg・l (1 – cos θ0 )
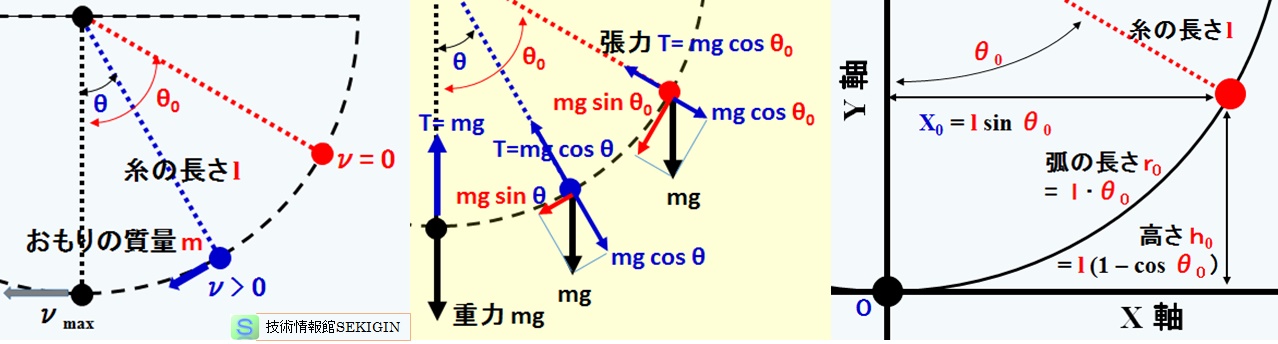
振り子の運動
ここでは,通常の X , Y軸ではなく,円弧に沿った軸 S を考える。この時,おもりに作用する接線方向の力は,おもりを S 軸の負の方向に運動させる力となる。加速度αはS軸方向の変位の時間による 2 階微分となるので,おもりの運動方程式は,
mα= m d2S/ dt2 = ‐F = ‐ mg sin θ
となり,加速度は
α = ‐g sin θ
で表される。
角度の単位ラジアン(radian , 単位記号 rad )の定義より,円弧の変位 S ,円弧の半径 l と角度θ(ラジアン,rad )は,
S = l θ
の関係にあるので,加速度は,
α = d2S/ dt2 = l d2 θ/ dt2 = - g sin θ = - g sin (S/ l )
と表される。すなわち,2 階微分は。
d2 θ/ dt2= - ( g/ l ) sin θ= - ( g/ l ) sin (S/ l )
と表すことができる。
これは,角速度(角度の変化)の変化の角加速度( rad・s‐2 )を与える式で,角加速度は重力加速度に比例するが,角度で変化することが分かる。
運動方程式の近似解
運動方程式に三角関数を含んでいるため,このままでは解を求められない。
そこで,円弧の長さ S と上図の X , Y軸における原点からおもりまでの距離 X の関係,
S = l θ,X = l sin θ
から,S と X の関係は,θ= 0.2443 rad (=14度)で S = 1.001 X ,θ=0.5235 rad (= 30度)で S = 1.047 X と,角度 30°以下で距離の差が 5% 未満に,角度 14°以下では 1 %未満の差となる。
そこで,実用上で距離の差が無視できるほどに角度θが小さい場合を考える。
この場合には,X ≒ S とでき,
sin θ = X/ l ≒ S/ l = θ
と置ける。
従って,おもりの運動方程式の近似式として,
d2θ/ dt2= - ( g/ l ) sin θ= - ( g/ l ) θ
と置けるので,A,Bを定数とした時,次の解がえられる。
θ= A sin ( g/ l )1/2 t +B cos ( g/ l )1/2 t
これを微分した角速度は,
dθ/ dt = A ( g/ l )1/2 cos ( g/ l )1/2 t – B ( g/ l )1/2 sin ( g/ l )1/2 t
と置ける。
従って,おもりの運動方程式の近似式として,
d2θ/ dt2= - ( g/ l ) sin θ= - ( g/ l ) θ
と置けるので,A,Bを定数とした時,次の解がえられる。
θ= A sin ( g/ l )1/2 t +B cos ( g/ l )1/2 t
これを微分した角速度は,
dθ/ dt = A ( g/ l )1/2 cos ( g/ l )1/2 t – B ( g/ l )1/2 sin ( g/ l )1/2 t
これを微分した角加速度は
d2θ/ dt2= - A( g/ l ) sin ( g/ l )1/2 t - B ( g/ l ) cos ( g/ l )1/2 t = - ( g/ l ) θ
となり,近似式からも運動方程式が導かれる。
A , B は,初期条件 t = 0 , θ= θ0 から,A = 0 , B =θ0と求まる。従って,運動方程式の近似式の解は,
θ= θ0 cos ( g/ l )1/2 t
となる。
ここで,( g/ l )1/2は, 角周波数ω( rad/ s )と呼ばれ,ωを 2 πで割った値が,1 秒間の繰り返し数,すなわち周波数 f ( Hz )になり,この逆数が周期 T ( s )になる。
f = ω/ 2 π= ( g/ l )1/2 / 2 π, T = 1/ f
近似式によると,おもりの周波数(周期)は,おもりと支点間の距離,すなわち糸の長さ l で決まり,角度に依存しないが,近似式が成立する角度を超える場合は,円弧上の距離 S とX , Y 座標上の X 成分との差が大きくなり,周波数(周期)は大きく(長く)なる。
ページの先頭へ
【弾性力(フック力)による運動(単振動)】
真空の無重力空間で,一端を固定し,他端に質量 m の物体をもつばねを,自然の長さを原点とし,X 軸の正方向に x だけ伸ばし,手を離した場合を考える。
物体に作用する力は,フックの法則に従い,自然の長さからの変位量 x (m)とばね定数 k (Nm‐1)とから
F = - kx
となる。
加速度 αとした時,ニュートンの運動方程式より
F = mα= - kx
α= d2x/ dt2 = - (k/ m) x
ここで,x = - sinθ,θ=(k/ m)1/2t とした時,
一階微分は,
dx/ dt = - dθ/dt・dsinθ/ dθ= - (k/ m) 1/2 cosθ
二階微分は,
d2x/ dt2 = - (k/ m) 1/2 dθ/dt・dcosθ/ dθ=(k/ m) sinθ= -(k/ m) x
となり,運動方程式の解が得られた。
一方,x = cosθ,θ=(k/ m) 1/2t とした時も,同様に運動方程式の解となる。
従って,弾性力(フック力)の運動方程式の一般解は,
x = A sin (k/ m) 1/2 t + B cos (k/ m) 1/2 t
とできる。
すなわち, (k/ m) 1/2は,振り子の運動の場合と同様に,角周波数ω( rad/ s )となり,
x = A sinω t + B cosω t
と書ける。ここで,三角関数の合成により,
x = ( A2 + B2 ) 1/2 sin (ωt + φ)
となる。なお,(A2 + B2) 1/2 は定数 C と置ける。この式は,初期位相φ,振幅 C(最大変位の絶対値)の単振動の式となる。
ωを 2 πで割った値が,1 秒間の繰り返し数,すなわち周波数 f( Hz )になり,この逆数が周期 T ( s )になる。
f = ω/ 2 π= (k/ m) 1/2 / 2 π, T = 1/ f
運動エネルギーと位置エネルギー
運動エネルギー K(x)は,
K(x) = 1/2・mν2 =1/2・m (dx/ dt)2
x = C sin (ωt + φ)
角周波数ω=(k/ m) 1/2
∴ K(x) = 1/ 2・ω2 C2 cos2 (ωt + φ) = 1/ 2・k C2 cos2 (ωt + φ)
となる。
ばねの位置エネルギーU(x) は,弾性エネルギー(1/ 2 k x2)である。
従って,位置エネルギーU(x)は,
U(x) = 1/ 2・k x2
x = C sin (ωt + φ)
U(x) = 1/ 2・k C2 sin2 (ωt + φ)
となる。運動エネルギー K(x) ,位置エネルギー U(x) とから全エネルギー E は,
E = K(x) + U(x) = 1/ 2・k C2 ( cos2 (ωt + φ)+sin2 (ωt + φ) )
ピタゴラスの定理より
E = 1/ 2・k C2
となり,力学的エネルギー保存則が成立する。
重力の影響を受けたばねの場合
地上で,垂直につるしたばねでは,重力の影響を受け,ばねの自然の長さを基準にした変位 x では,
E = 1/2・mν2 +1/2・k x2‐mgx = 一定
重力の影響を受けて,釣り合った状態の長さを基準にした変位 y では,
E = 1/2・mν2 +1/2・k y2 = 一定
とできる。
なお,弾性力と重力の和(‐kx + mg = ‐ky )が釣り合いの位置を基準とした場合に働く力となる。
ページの先頭へ