物理 第四部:波・波動の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,音,光などの波の理解に資する基礎として, 【波動の基礎分類】, 【波動の基本式】, 【ホイヘンスの原理,速度とは】, 【反射,屈折,回折】 に項目を分けて紹介する。
【波動の基礎分類】
物理的には空間を伝わる振動(oscillation , vibration)を波(wave)や波動(wave , wave motion)といい,波と波動は,同じ意味合いを持つが,一般的に持たれるイメージには差異が見られる。
一般的に波という場合は,海,湖や川で風や震動で引き起こされる水面の高低運動を指す場合が多い。流体力学では,水面の高低運動の波は,重力波(gravity wave),表面波(surface wave)や水面波などという。
波動と称する場合は,重力波に限らず,空間や物体の一部において発生した振動などの変化が周囲に次々と伝わる現象を意味する場合が多い。
一般的に,波動を扱う分野では,物理現象として音や光などの振動(周期的な現象)が扱われる場合が多い。しかし,周期性は波動に必須の性質ではない。このため,波動では,振動が連続的に発生し伝搬する連続波(continuous wave),単独もしくは短い振動が伝搬するパルス波(pulse wave)に分類して扱われることが多い。
また,地震波(seismic wave , earthquake wave)の解説で,p 波,s 波に分けて説明されるように,波動は,媒質の振動が波の進行方向に対して平行な縦波(longitudinal wave)と波の進行方向に対して垂直な横波(transverse wave)に分けられる。
身近なものでは,光を含む電磁波(electromagnetic wave)は,媒質(真空,電磁波に対し透明な物体)中の電場と磁場の変化によって形成される横波である。
空気など気体を媒体とする音波(acoustic wave)は,圧力変化で発生する疎密波(compressional wave)ともいわれる縦波である。
波として最も身近な,水面で観察される重力波は,一見すると,媒質(水)の上下運動により進む横波と思われがちだが,重力波(表面波)で紹介するように,重力を復元力とする水粒子の楕円運動により位相が進む波で,厳密には横波とは区別されるべき波である。
地震波などの弾性体を媒質とする音波(弾性波)には,縦波と横波が存在する。地震波の P 波(P-wave)は,第一波(Primary wave)や圧力波(Pressure wave)の頭文字で,疎密波ともいわれる縦波である。
S 波(S-wave)は,第二波(Secondary wave)やせん断波(Shear wave)の頭文字で,進行方向と直角に振動する横波である。
なお,断層破壊の地震では S 波の振幅は大きいが,地下核実験などによる振動では理論上では S 波が発生しない。このため,地盤振動の測定結果は,核実験の有無の傍証となりうる。
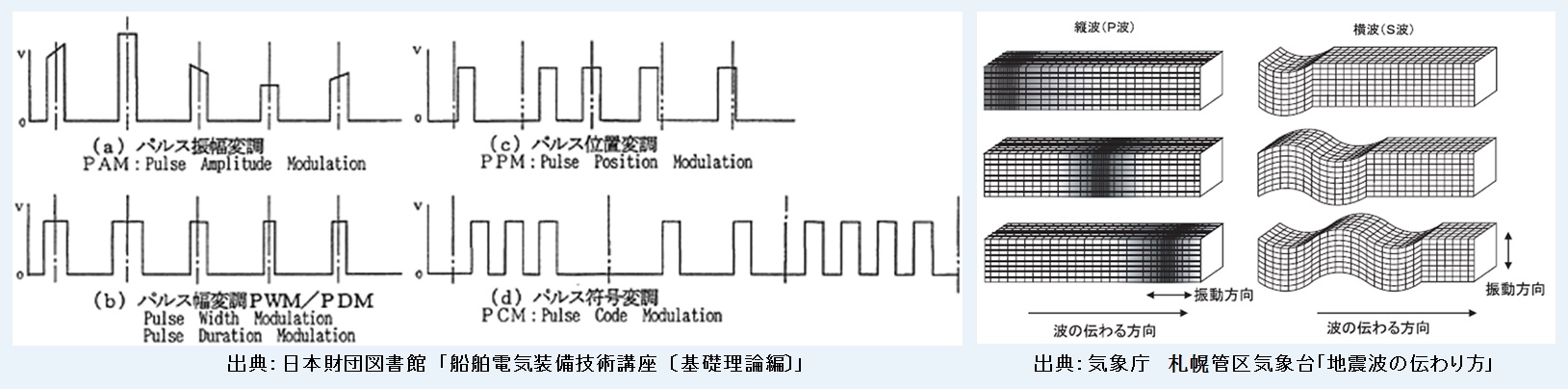
波動(パルス波,縦波,横波)とは
出典:左図(日本財団図書館),
右図(気象庁 札幌管区気象台; 2018年参照の図,2021年時点で削除)
- 弾性波(elastic wave)
音波や地震波などの弾性体内を伝わる波をいう。
弾性体が固体の場合は,変位方向により,体積変化に伴う体積弾性による縦波,体積変化がなく形状変化に伴う形状弾性による横波に分けられる。
弾性体が流体の場合は,密度変化(体積変化)に伴う縦波だけで,横波はない。
ページの先頭へ
【波動の基本式】
速さ c で媒体中の x 方向にのみ伝搬する波を考える。この波の y 方向の変位は,ある点での時間経過を考える式,空間中の 2 点間の距離を考える式で表せる。
空間中の一点に注目し,時間経過による表現
時刻= 0 の時の初期波形 y = f (x) の波が,時刻 = t には初期波形を x 方向に ct だけずらしたものと考えられるので,
y 方向の変位は,
y = f (x – ct)
で表される。
空間中の二点間の距離による表現
空間中の任意に選んだ点での振動を y = F (t) とした時,この点から x だけ離れた点の y 方向の変位は,時間 x/ c だけ遅れて振動すると考えられるので,
y = F (t – x/ c)
として表される。
波動は,単振動合成で紹介した重ね合わせの原理が成り立つので,x 方向のプラス方向とマイナス方向に伝わる 2 つの波動があるとき,任意の点 x での変位 y は,
y = f (x – ct) + g (x + ct)
又は,
y = F (t – x/ c)+ G (t + x/ c)
で与えられる。
一般的に観察される正弦波では,振幅 a とした時,
![]()
あるいは,
![]()
で与えられる。なお,∓ は,上述の通り x 方向に対す進む方向により選ばれる。
ここで,波長 λ,周期 T ,振動数(周波数)ν,角振動数(角周波数)ωとの関係は,
![]()
なので,例えば,
![]()
のようにいろいろの形で書くことができる。
波動方程式について
前述の合成波の式
y = f (x – ct) + g (x + ct)
は,任意の時刻 t である点 x での媒質の変位を示すことを紹介した。
式には,波の形はいろいろあり,振動数も波を起こす方法により異なるなどの情報が含まれる。
これを x ,t でそれぞれ 二階微分(偏微分)すると,
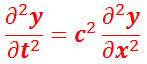
が得られる。
この偏微分方程式(partial differential equation)を波動方程式(wave equation)といい,波を起こす方法に関する情報が含まれず,速さ c だけを含む波に共通な性質のみが示される。
例えば,【音波(弾性波)】で紹介するように,
弦を伝わる横波:張力 S ,単位長さの質量ρのとき,c2 = S/ ρ
棒を伝わる縦波:棒のヤング率 E ,密度ρのとき,c2 = E/ ρ
空気を伝わる縦波(音波):体積弾性率 K ,密度ρのとき,c2 = K/ ρ
となる。
【参考:基礎用語】
- 二階微分(second derivative)
二度微分ともいい,関数の導関数(一階微分したもの)をさらに微分したもので,例えば,d2 y/ dx2 で表す。偏微分の二階微分は,𝜕 2 y/ 𝜕 x2 と表し,導かれたものを二次導関数という。
例えば,変位の時間の一階微分は速度(変位の変化割合)を,二階微分は加速度(速度の変化割合)を意味する。 - 偏微分(partial differential)
二つ以上の変数を持つ関数 f において,一つの変数にだけ注目し,他の変数は固定して定数とみなし,注目した変数の関数として微分することをいう。例えば,関数 f を x で偏微分するという場合は,関数 f の偏微分 𝜕 f/ 𝜕x と表す。 - 波動方程式(wave equation)
波動に関する運動方程式で,空間座標と時間とを独立変数とする波を記述する偏微分方程式をいう。
ページの先頭へ
【ホイヘンスの原理】
以上までの説明では,一直線上を伝わる波を想定していたが,実際の波は空間を伝わる。
空間を伝わる波の特徴の理解に資する基本的性質の概要を次に紹介する。
波の基本区分
空間を波動が伝わるとき,その位相の等しい点を連ねた面を波面(wave front)といい,波面が球面の波動を球面波(spherical wave),平面ならば平面波(plane wave)という。
波動の伝わる方向は,波面に垂直な方向である。この波動の進む線を射線(ray)という。
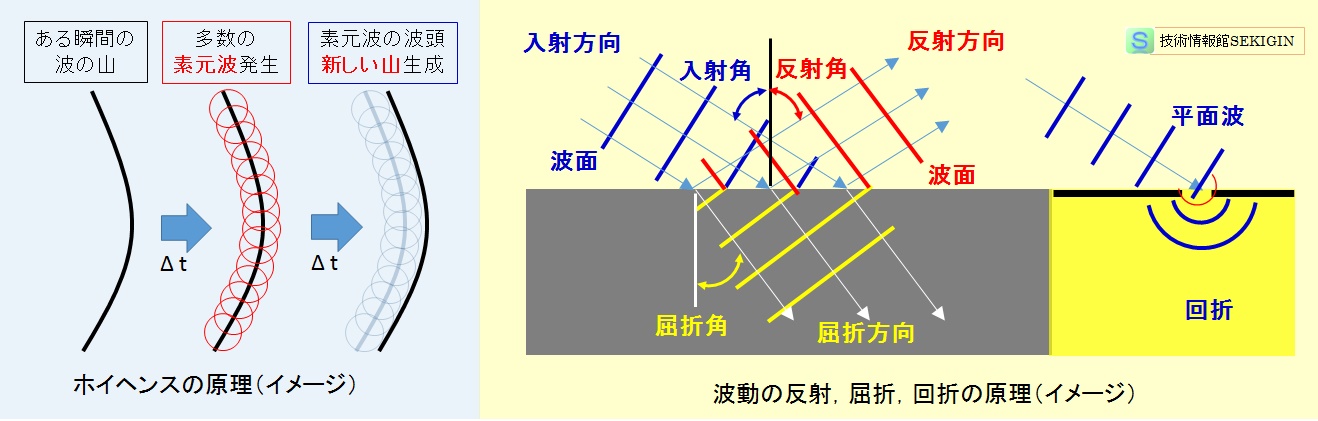
ホイヘンスの原理(Huygens’ principle)
ある瞬間の波面が与えられているとき,短い時間経過後の新しい波面を知るために用いられる。
ホイヘンスの原理は,オランダの物理学者ホイヘンスが唱えた波の伝播に関する仮説である。
『注目するある瞬間の波面上のすべての点が新しい波原となり,同じ速さ,同じ振動数の二次波(素元波;elementary wave)が球面波として送り出される。個々の素元波を観察することはできないが,全ての素元波に接する曲面(包絡面:envelopment surface)が,その時刻の波面として観察される。この現象が次々と起こり波面が波の進行方向に進む。』
ホイヘンスは,この仮説により,光の直進,反射,屈折の現象を説明したが,当初の仮説には,いくつかの欠点があった。その後,1818年にフレネルが欠点を修正したため,ホイヘンスの原理は,ホイヘンス‐フレネルの原理(Huygens–Fresnel principle)ともよばれる。
波動の速度
波動の速度には,位相速度(phase velocity)と群速度(group velocity)がある。位相速度とは,波の山や谷の特定の位置が移動する速度のことで,伝播速度(でんぱそくど)ともいわれる。
複数の波を重ね合わせた時に,その全体(波束)が移動する速度は群速度と呼ばれる。
分散がない場合には,位相速度と群速度 は一致する。
波動の基本特性
- 波動方程式(wave equation)
波動に関する運動方程式で,空間座標と時間とを独立変数とする波を記述する偏微分方程式をいう。 - ホイヘンス(Christiaan Huygens)
クリスティアーン・ホイヘンス(1629年~1695年)は,オランダの数学者,物理学者,天文学者,1690年に光の波動説を提唱する『Traite de la lumiere:光についての論考』を発刊。 - フレネル(Augustin Jean Fresnel)
オーギュスタン・ジャン・フレネル(1788年~1827年)は,フランスの物理学者,土木技術者,光の波動説を唱え,光の回折や複屈折現象などの理論研究,灯台や投光器に用いるフレネルレンズの発明など光学分野で業績を残す。 - 球面波(spherical wave)
三次元の等方媒質中において,ある一点(波源)を中心とし,放射状に広がる波,又はある一点に向かって収束する波で,球対称の波となる。なお,波源から遠ざかると,球面は平面に近づき,遂に平面波になる。 - 平面波(plane wave)
波面が波の進行方向に垂直な平面上にある波をいう。波源からきわめて遠く離れている球面波は近似的に平面波とみなすことができる。 - 素元波(elementary wave)
ホイヘンスの原理における前進する波面の各点から出る小さな無数の球面波。 - 包絡線(envelope)
平面上の曲線群のすべてに接する曲線を,曲線群の包絡線という。 - 包絡面(envelopment surface)
空間内の曲面群のすべてに接する曲面を,曲面群の包絡面という。
ページの先頭へ
【波の反射,屈折,回折】
反射(reflection)
波動が1つの媒質から他の媒質へ向って伝搬するとき,媒体の境界面(界面)で一部分又は全部がもとの媒質内へ戻る現象をいう。全部戻る場合を全反射(total reflection)という。
波の反射では,入射面内で法線に対して,入射と反対側に反射し,入射角と反射角は相等しい。これを波の反射の法則(law of reflection)という。
波の反射による位相の変化
波の進む媒質に端部において,波の変位が自由な場合と変位が困難な場合がある。
例えば,空気中に置かれた棒を伝わる縦波を考える。棒の端部が自由に動ける場合は,伝播した波による棒の端部の変位が可能である。このような端部を自由端(fee end)という。
一方,棒の端部を動けないように固定した場合には,端部に達した波による変位が困難となる。このような端部を固定端(fixed end)という。
自由端での位相の変化
入射した波により変位するが,ひずみ(棒の内部応力)はゼロでなければならない。このことは,入射波と反射波を合成した変位が常に極大又は極小となる。
すなわち,入射波と同じ形状の波が反対向きに進んできたように振る舞い,反射波は入射波が端部で折り返したと考えることができるので,波の位相は変化しない。
固定端での位相の変化
端部が拘束され,波では端部が変位できない。このことは,端部における入射波と反射波の合成波の変位がゼロであることを意味する。従って,固定端において,反射波は入射波と位相がπだけ変化している。
屈折(refraction)
波動が進む 1 つの媒質から他の媒質の中に入り込む場合に,その界面で進行方向が変化する現象をいう。
物質を構成する結晶の分子・イオンの空間分布が方向に依存しない等方性媒質の間での屈折では,入射角 i と屈折角 r との間にスネルの法則(Snell's law)が成り立つ。
スネルの法則は,屈折の法則ともいわれ,媒質中の波動の位相速度(νi ,νr ),入射角( i ),屈折角( r )の関係を表した法則で,ホイヘンスの原理によって説明できる。
sin i / sin r =νi / ν r = 一定(相対屈折率)
回折(diffraction)
媒質内を伝わる波動が,障害物の後方の影の部分まで回り込む現象である。波の波長が大きいほど,顕著な回折がおこる。
例えば,音波や長波長の電磁波では,障害物の影に回り込む現象を容易に体感できる。可視光ほどの波長の短い電磁波では,体感できるほどの回析現象は観察し難い。しかし,周期的に並んだ格子(回折格子)を用いることで,回折した電磁波の干渉縞を観察することができる。この原理は,光や X 線の分光分析(赤外分光分析,発光分光分析,蛍光 X 線分析など)に用いられている。
界面(interface)とは,一般的には気体,液体や固体などの基本的な物質の状態(三態や三相という)が接している境界面を指すことが多い。物理的には,これに加えて,ある均一な相が他の均一な相と接している場合の境界を含む。
すなわち,対象となる境界には,気相―液相,気相-固相,液相―固相の境界面の他に,同じ状態の物質でも分子組成や密度が異なる気相間,液相間,固相間の接触境界面も含む。
【参考:基礎用語】
- 反射の法則(law of reflection)
光の波長に比べてなめらかな2媒質の境界面で反射するとき成り立つ法則。1.入射光線と反射光線は入射点で媒質の境界面に立てた法線と同じ平面上にあり,かつ法線に関して反対側にある。
媒質1を経て入射した光線が他の媒質2との境界面で反射するとき,境界面の法線に対して θ の角度で入射した光線は入射面内で法線に対して -θ の角度をなす方向に反射される。すなわち反射において入射角と反射角は等しく逆符号であることを反射の法則という。 - スネルの法則(Snell's law)
屈折の法則(laws of refraction),デカルトの法則(Descartes' law)ともいわれ,光が二つの媒質の境界面で屈折するとき,入射角の正弦と屈折角の正弦との比(屈折率)は一定で,その値は二つの媒質のみによって定まるという法則。
オランダの天文学者スネルが発見し,フランスの哲学者デカルトがまとめた法則である。 - スネル(Willebrord Snell)
ヴィレブロルト・スネル(1580年~ 1626年)は,オランダの天文学者,数学者でスネルの法則(光の屈折)で知られる。 - デカルト(René Descartes)
ルネ・デカルト(1596年~ 1650年)は,フランス生まれの哲学者,数学者で,合理主義哲学の祖(近世哲学の祖)として知られる。
ページの先頭へ