物理 第一部:物理学とは
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,運動の基本として,【等加速度運動とは】,【等速直線運動】,【等加速度直線運動】,【放物運動】,【摩擦抵抗,空気抵抗の影響】に項目を分けて紹介する。
【等加速度運動とは】
等加速度運動(motion of uniform acceleration)とは,加速度が一定の運動で,一定の大きさと方向をもつ力を受けているときの運動をいう。
地表表面では,重力(gravity)は近似的に均一で一定と考えられるため,地表近くの物体の運動は等加速度運動と考えて差し支えない。
また,一様な電場の中での電荷を持った物体に対する静電的な影響に比較し,地球の重力の影響が無視できるほど小さいので,等加速度運動とみなして差し支えない。
等加速度運動では,物体の初速度がゼロ,又は加速度の方向と初速度の方向との成す角度が 0 度,又は 180 度の場合は,物体は一直線上を移動する直線運動となる。
一方,初速度の方向と加速度の方向の成す角度が 0 ,180 度以外の場合は,移動の軌跡が放物線を描く。
なお,重力場での運動は,直線運動を含めて放物運動といわれる。
直線運動(linear motion)
直線運動は,等速直線運動と等加速度直線運動に分けられる。
等速直線運動(uniform linear motion , linear uniform motion)は,等速度運動ともいい,加速度ゼロ(摩擦や引力などの外力を受けない状態)の時の運動で,初速度の方向に慣性の法則(law of inertia)に従い直線上を一定速度で運動する。
等加速度直線運動(uniform acceleration linear motion , linear motion of uniform acceleration)は,ゼロではない一定の加速度を受け続ける物質の運動であるが,初速度の方向との関連で 2 種に分けられる。
初速度がゼロの場合を含み加速度と初速度が同じ方向の場合(例えば真空中の鉛直下方投射),加速度と初速度が反対の方向の場合(例えば真空中の鉛直上方投射)である。
放物運動(projectile motion)
放物運動とは,一様な力(重力など)の加わる空間に投げ出された物体の運動をいう。直線運動(自由落下,鉛直下方投射,鉛直上方投射)も含まれるが,一般的には,運動の軌跡が放物線を描く水平投射や斜方投射など投げ出す方向と力の方向との成す角度が 0 ,180 度以外の方向に投げ出された物体の運動をいう場合が多い。
【参考:基礎用語】
- 速さと速度
速さはスカラーで,速度はベクトルである。従って,等速直線運動は同じ速さで直線上を運動,等速度運動は同じ速さで定まった方向(直線)に運動と同じ意味になるが,誤って等速度直線運動と記した場合は同じ速さで定まった方向(直線)に直線上を運動と重複表現になるため,日本語として不適切である。また,等速運動とした場合は,方向に言及しておらず直線状の運動とは限らないので,等速度運動とは異なる。 - 慣性の法則(law of inertia)
ニュートン力学の運動の第一法則で,“物質の外から力が作用しない限り,質点は静止または等速直線運動する” と定義されている。
ここで,“物体の外から力が作用しない限り” を厳密に表現すると,物体に外から力が作用していない場合の他に,物体に作用している力が釣り合っている場合(力の和ベクトルがゼロ)を意味する。 - ストークスの式(Stokes' law)
流体中を沈降する微粒子の終端速度を表す式で,沈降法による粒子径測定などに用いられている。 - 終端速度(terminal velocity)
重力場において,浮力や抗力などの粒子に作用する上向きの力と下向きの重力とが釣り合ったときの速度である。
浮力は粒子の速度に依存しないが,抗力は粒子と流体の相対速度に依存するため,落下速度の増加と共に抗力が増加する。
ページの先頭へ
【等速直線運動】
等速直線運動(uniform linear motion , linear uniform motion)は,等速度運動ともいわれ,物体が慣性の法則に従う運動のため,初速度 ![]() の大きさと方向が維持される。すなわち,任意にとった移動距離 X と移動に要した時間 t に次の関係が成立する。
の大きさと方向が維持される。すなわち,任意にとった移動距離 X と移動に要した時間 t に次の関係が成立する。
![]() = X / t
= X / t
すなわち運動方程式は,
X =![]() t
t
ここで,![]() は一定
は一定
となる。
これを変位と時間の図(x-t 図),速度と時間の図(v-t 図),加速度と時間の図(a-t 図)で表すと下図のようになる。すなわち,外力を受けないので,加速度ゼロで,初速度が維持され,時間に対し一定の割合で変位する運動となる。
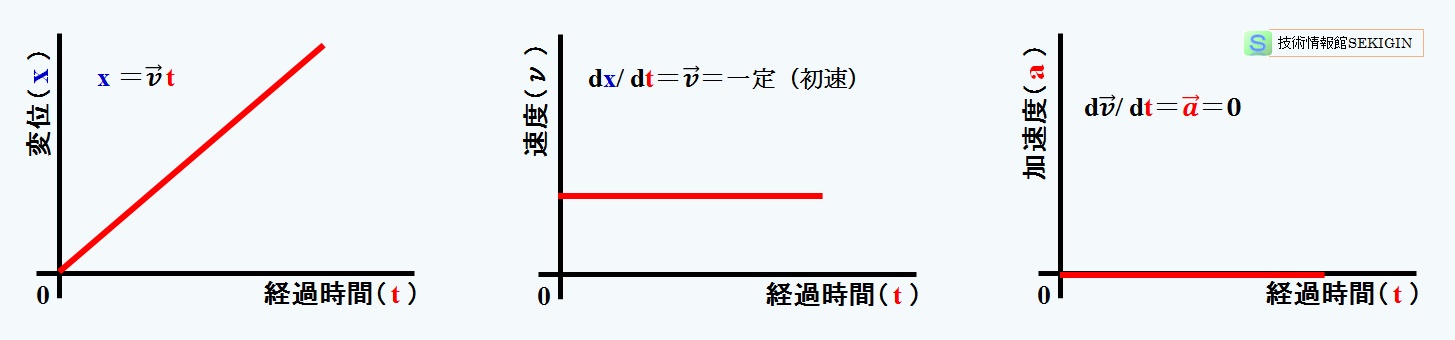
等速直線運動のグラフ
ページの先頭へ
【等加速度直線運動】
等加速度直線運動(uniform acceleration linear motion , linear motion of uniform acceleration)とは,ゼロではない一定の加速度を受け続ける物質の直線運動であるが,初速度により 2 種に分けられる。
初速度がゼロの場合を含み,加速度と初速度が同じ方向の場合(例えば真空中の自由落下(free fall)や鉛直下方投射),加速度と初速度が反対方向の場合(例えば真空中の鉛直上方投射)が主な例として挙げられる。
他の例として,直進する乗り物が一定の動力,又はブレーキ力を受けて加速する場合(ただし,摩擦や空気抵抗を無視した場合)などもある。
すなわち,初速度![]() ,加速度
,加速度![]() を一定とした時,任意にとった移動距離 X と移動に要した時間 t に次の関係が成立する。
を一定とした時,任意にとった移動距離 X と移動に要した時間 t に次の関係が成立する。
X =![]() t + 1/2・
t + 1/2・![]() t2
t2
これを微分すると,速度が得られる。
dX /dt=![]() =
=![]() +
+![]() t
t
ここで,t を消去すると,等加速度直線運動の式が得られる。
![]() 2-
2-![]() 2= 2
2= 2![]() ・X
・X
ここで,![]() ,
,![]() は一定
は一定
直線運動では,初速度の向きと加速度の向きが一致る場合と反対向きの場合がある。これを,変位と時間の図(x-t 図),速度と時間の図(v-t 図),加速度と時間の図(a-t 図)で表すと下図のようになる。
初速度と加速度が同じ向き(速度と加速度の符合が一致)
時間に対し変位の変化量が大きくなり,速度が増加し続ける。
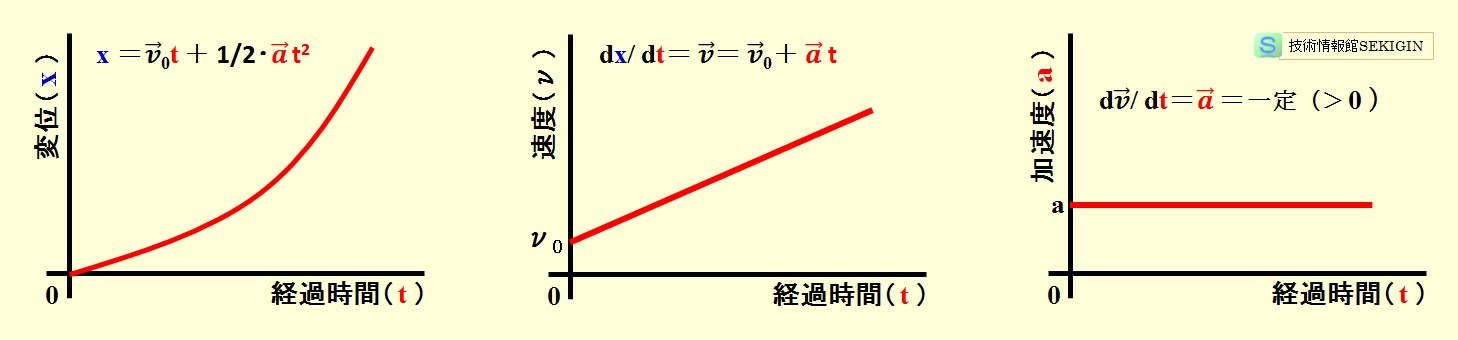
等加速度直線運動(速度と加速度が同じ向き)のグラフ
初速度の向きと加速度が反対向き(速度と加速度の符合が反対)
初速度の方向を正とし,加速度の符合を負とした時の変位と時間の図は,頂点を持つ放物線を描き,速度が減少し放物線の頂点で速度ゼロとなる。その後,速度の符合が逆転(加速度と速度の方向が一致)し,速度の増加が続く。
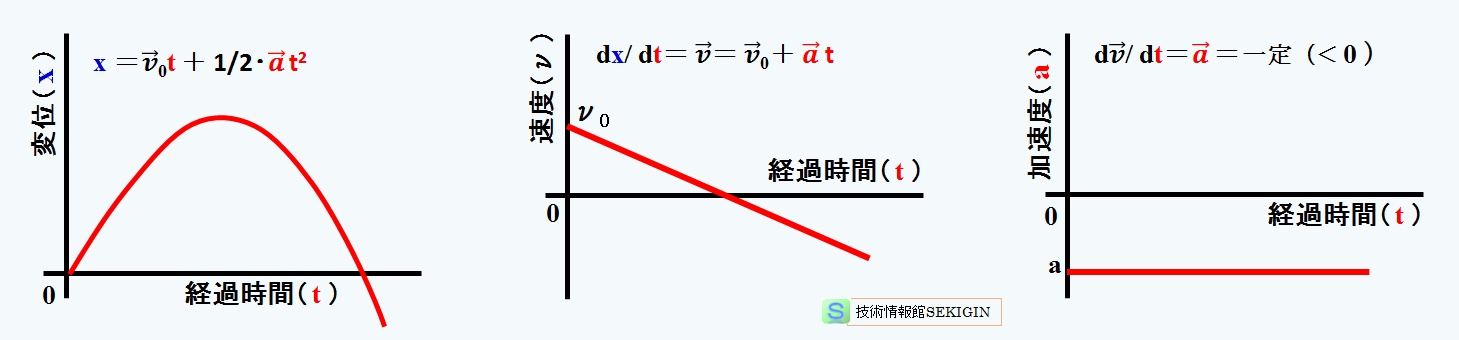
等加速度直線運動(速度と加速度が反対向き)のグラフ
ページの先頭へ
【放物運動】
放物運動(projectile motion)とは,一様な力(重力など)の加わる空間に投げ出された物体の運動をいう。
放物運動は,重力(gravity)に対し投げ出される方向と初速度の違いにより,自由落下,鉛直下方投射,鉛直上方投射,水平投射,斜方投射に分けられる。
なお,自由落下,鉛直下方投射,鉛直上方投射は,等加速度直線運動で紹介した。
ここでは,地球上で質量 m の物体(質点)が,地表面と成す角度θで初速度![]() で投げられたとする。空気抵抗を無視した場合に,この物体には,重力加速度 g がつねに垂直方向にのみ作用する。
で投げられたとする。空気抵抗を無視した場合に,この物体には,重力加速度 g がつねに垂直方向にのみ作用する。
x,y 座標で考えると,ベクトルである初速度![]() は, x 成分(水平方向)と y 成分(鉛直方向)に分解できる。
は, x 成分(水平方向)と y 成分(鉛直方向)に分解できる。
すなわち,水平方向には![]() cosθの等速直線運動,鉛直方向には初速度
cosθの等速直線運動,鉛直方向には初速度![]() sinθの等加速度直線運動に分けることができる。
sinθの等加速度直線運動に分けることができる。
従って,x,y方向の速度と経過時間( t )の関係は,
νx=![]() cosθ
cosθ
νy=![]() sinθ‐g t
sinθ‐g t
で表せる。
これにより,質点の位置の座標は,速度の時間積分により次のように表せる。
x =![]() cosθ・ t
cosθ・ t
y=![]() sinθ・ t ‐1/2・g t2
sinθ・ t ‐1/2・g t2
この二式より,t を消去すると,運動の軌跡を表す式が得られる。
y=‐1/2・g・(![]() cosθ)‐2・ x2+ tanθ・ x
cosθ)‐2・ x2+ tanθ・ x
θ=‐90°,90°の場合は,x = 0 で前出の等加速度直線運動の自由落下,鉛直下方投射,鉛直上方投射になる。θ= 0°の場合は水平投射,その他の角度の場合は斜方投射という。なお,軌跡が放物線を描く斜方投射は 0 <θ< 90 ,90 <θ< 180 の場合である。
水平投射(cos 0 =1,sin 0 = 0 )の x軸方向の速度と位置は,νx=![]() ,x=
,x=![]() t と等速直線運動していることが,y軸方向の速度と位置は,νy=‐g t ,y=‐1/2・g t2と初速度ゼロの場合の等加速度直線運動,すなわち自由落下していることが分かる。
t と等速直線運動していることが,y軸方向の速度と位置は,νy=‐g t ,y=‐1/2・g t2と初速度ゼロの場合の等加速度直線運動,すなわち自由落下していることが分かる。
すなわち,放物運動は,x軸の等速直線運動とy軸の等加速度直線運動の合成で説明できることが分かる。
下図に示すように,図示する場合は,y 軸の正を天面方向とするか地面方向とするかの決まりが無く,説明に応じて適切に選択するのが一般的である。
この時に,速度と加速度の関係が分かるように符号を変えなければならない,例えば,天面を正にする場合は,重力加速度が地面を向くので,負の値にしなければならない。
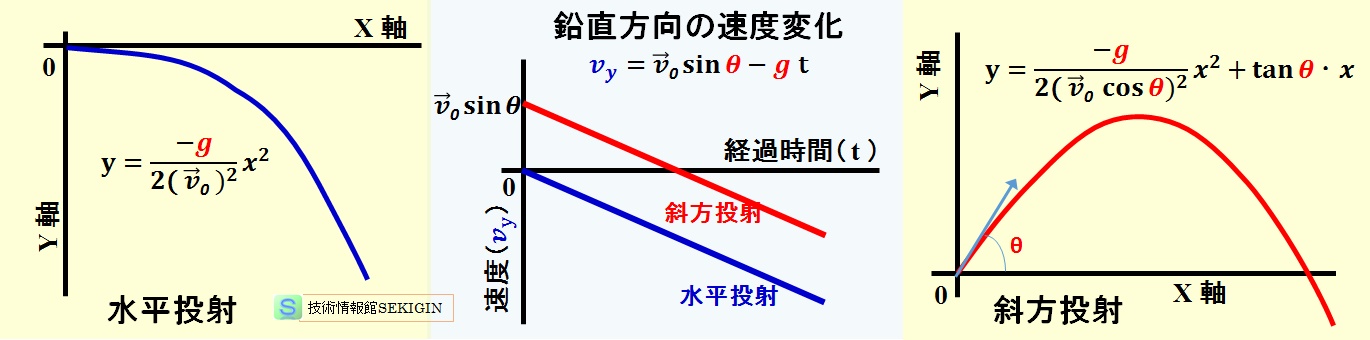
水平投射,斜方投射における物体の軌跡
ページの先頭へ
【摩擦抵抗・空気抵抗の影響】
物体 A と物体 B が接触する場合は,その界面で,作用・反作用の法則に従い,物体 A に加えた力と反対方向の力が接触面に沿って発生する。この力が摩擦力(force of friction)である。
固体同士の接触による摩擦力は,静止している物体 A に力を加えた時に物体 B との接触面に加えた力と反対方向に発生する同じ大きさの静止摩擦力(static Friction)と運動している物体 A との接触面に加えた力と反対方向に発生する加えた力より小さい動摩擦力(dynamic Friction)に分けられる。
摩擦力 F は,物体 A の重量・荷重などの垂直抗力 P ,接触面の状態に応じた摩擦係数μに比例し,見かけの接触面積や速度には依存しない。
F = μP
静止摩擦係数は動摩擦係数より大きいため,動かし始める力に比べ,動かし続ける力は小さくすむ。物体が動き出す直前の力を最大静止摩擦力(最大摩擦力)という。
固体と流体の接触の場合は,流体の粘性に起因して生じる力を粘性摩擦力という。粘性摩擦力は,固体同士の動摩擦力とは異なり,相対速度に比例した力である。
空気抵抗(air resistance , aerodynamic drag)
空気中を物体が移動するとき,又は空気の流れにあるとき,移動方向や空気の流れの方向と反対方向に生じる抵抗力を空気抵抗という。
一般的には空気抵抗というが,空気に限らず気体・液体などの流体に共通するので,物理学では抗力(drag)という。流れの方向に対し。垂直方向の成分を揚力(lift)ともいう。
空気抵抗の大きさは,物体の形,大きさ,速さで変化し,一般化するのは困難といわれている。主要な空気抵抗は,物体の形状に依存する圧力抵抗(pressure drag),摩擦抵抗(friction drag)である。圧力抵抗は慣性抵抗(inertial resistance)ともいわれ,物体表面に垂直に働く圧力の合力から成る抵抗で,摩擦抵抗は粘性抵抗(viscous drag)ともいわれ,進行方向と平行の表面に働く空気の粘性力の合力から成る抵抗である。
摩擦抵抗(粘性抵抗)は,概ね速度に比例し,圧力抵抗(慣性抵抗)は,概ね速度の 2 乗に比例する。圧力抵抗と摩擦抵抗は,物体の形状に依存するのでまとめて形状抵抗(form drag)ともいわれ,一般的には速度のほぼ 2 乗に比例する例が多い。
高等学校教育では,空気抵抗は速度に比例(R=![]() )と紹介しているが,これは,雨滴など小さな球体が流体中を沈降する際の終端速度を表すストークスの式(Stokes' law)を導く際の仮定で,空気抵抗の影響を理解させる目的で使用されている。
)と紹介しているが,これは,雨滴など小さな球体が流体中を沈降する際の終端速度を表すストークスの式(Stokes' law)を導く際の仮定で,空気抵抗の影響を理解させる目的で使用されている。
ストークスの式が成立するのは,圧力抵抗を考慮しなくともおすむ条件,すなわち物体の寸法が小さい,流体の密度が小さく粘性が高いなどレイノルズ数(Reynolds number)が1 より小さいなどの場合である。
従って,高等学校教育では,実際に起きる多くの現象(空気抵抗を考慮した運動)とは異なることを念頭に置いて解説することが望まれる。
ページの先頭へ