物理 第六部:電磁気学
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,交流電気回路理解に必要な基礎を, 【交流とは】, 【正弦波交流の特徴】, 【コンデンサと交流(リアクタンス)】, 【コイルと交流(リアクタンス)】, 【インピーダンスとは】, 【交流電力とは】, 【正弦波交流の電力】 に項目を分けて紹介する。
【交流とは】
交流(alternate current)
略語 AC で表される交番電流であるが,省略して交流と称するのが一般的である。交番電流とは,時間の経過とともに大きさと向きが周期的に変わる電流をいい,電圧の場合は交流電圧(ac voltage)という。
しかし,単に交流という場合は,交流電圧と交番電流の区別なく用いる場合が多い。この場合は,交流信号ともいわれる。
典型的な交流の波形は,発電所の発電機から供給される正弦波のため,狭義の交流は正弦波交流(sinusoidal alternating current)を指す。
広義の交流は,正弦波に限らず周期的に大きさと向きが変化する非正弦波交流(non-sinusoidal alternating current)も含む。
代表的な非正弦波交流には,波形が方形の矩形波(square wave),三角形の三角波(triangle wave),のこぎりの歯形に似たのこぎり歯状波(sawtooth wave),短時間に急激に変化(脈動)するパルス波(pulse wave)などがある。
パルス波の中で,ごく短時間に回路に流れる衝撃電流をインパルス(impulse)という。
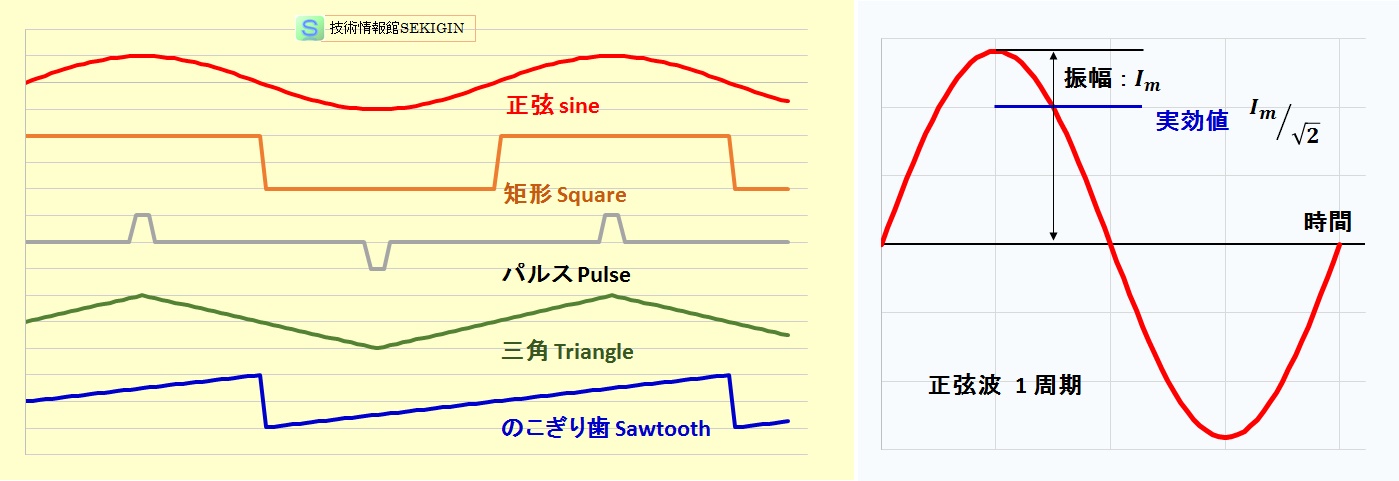
交流の代表的な波形
磁界中でコイルを一定速度で回転させると,フレミングの右手の法則により導かれる方向に起電力を生じる。起電力の方向は,コイルの回転角に応じ,周回の前半と後半で正負が逆転する正弦波(サイン波)の波形を持つ。
直流発電
大きな電力の実用化のために,フランス人技術者ヒポライト・ピクシーが初の整流子発電機(ダイナモ,dynamo)を開発した。アメリカの発明家エジソンが直流発電・直流送電を推進したが,交流発電・送電が優勢となり,大規模な直流発電は実現されなかった。
発電機の基本的な構成は,下図の左端に示すように,回転体の周辺に導体(コイル)を設け,磁束の間を回転させる。電磁誘導でコイルに発生した起電力は,コイルが 180 度回ると正負が逆になる。
このため,回転体と一緒に廻るスイッチ(回転電気スイッチ,整流子)として,それぞれの導体の一端に半割りした金属円筒を接続し,金属の円筒と導体が同じ軸で回転する。
金属円筒の上に接触してすべるブラシを設けることで,回転円筒とブラシを通して脈動する直流電圧が供給される。
交流発電
原理的には,下図の中央に示すように,直流発電機の回転電気スイッチ(整流子)を除き,コイルに誘起する電圧を,導体の端に取り付けた金属円筒とブラシを通じて取り出すことができる。取り出された電圧は,半回転毎に正負を繰り返し,正弦波を描く。
発電所や工場などの比較的大きな電力を必要とする場合には,下図の右端に例示するように,コイルを固定し磁石を回転させる構造でブラシ接触をなくした回転界磁型構造の発電機が採用されている。
大電流の発電が求められる大規模発電所では,永久磁石より大きな磁力が得られる電磁石を回転磁石に用いている。
回転界磁型発電機から取り出される電流は,周期的に流れる向きが変わる交流波形を描くが,コイルの配置により,単相交流発電,二相交流発電,三相交流発電がある。 コイル 1 つで 1 系統の電力を取り出す(単相交流発電)より,3 つのコイルを用い,1 つの回転子の回転エネルギーから 3 系統の電力を取り出す方が発電効率を上げられるため,発電所では三相交流発電が採用されている。
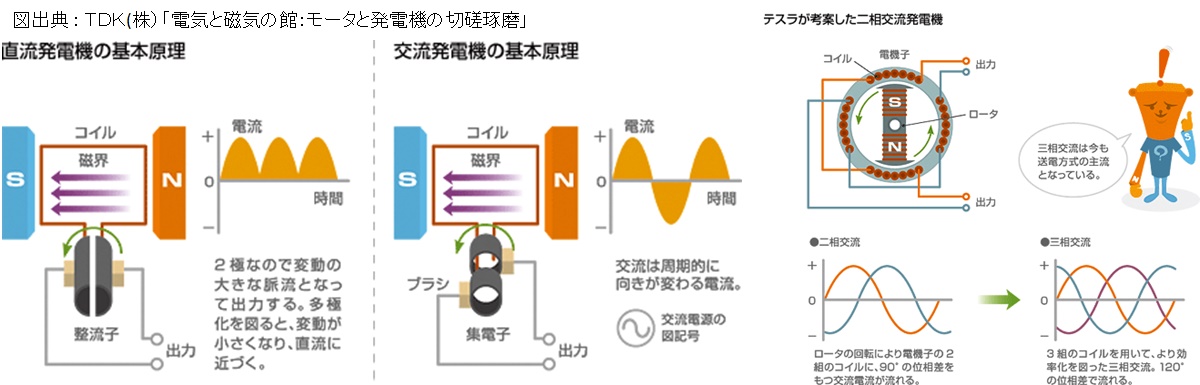
発電の原理
図出典:TDK(株)「電気と磁気の館:モータと発電機の切磋琢磨」
【参考:基礎用語】
- 波動(wave motion)
空間のある点で生じた変化(振動など)が隣接する部分に次々と有限の速さで伝わる現象で,波ともいわれる。波動の性質は,周期,振幅,波長などで表され,反射,屈折,干渉,回折などの現象を示す。 - パルス波(pulse wave)
パルス(Pulse)は,脈動ともいわれ,短時間に急峻な変化をする信号の総称である。
物理学では,連続波の対義語としても用いられる。代表的なパルス波形には,矩形波 (方形波) ,三角波,鋸歯状波,半正弦波,ガウス波などがある。 - 正弦波(sine wave , sinusoidal wave)
波形が正弦曲線(サインカーブ,sine curve)として観測可能な周期的変化を示す波動で,数学,信号処理,電気工学やその他の分野において重要な働きをする。正弦曲線は,シヌソイド(sinusoid)とも呼ばれる。 - フレミングの右手の法則(Fleming's right hand rule)
外部磁場内を運動する導体内に発生する起電力(電磁誘導)の向きを覚えやすくするためにフレミングが考案した方法である。
右手の中指と人差し指と親指をたてて互いに直角の関係にしたとき,人差し指が磁力線の方向,親指が導体の動いた方向,中指が導体に発生する起電力による電流の方向を向く。 - ヒポライト・ピクシー(Hippolyte Pixii)
ヒポライト・ピクシー(1808 ~ 1835年)は,フランスの技術者で,ファラデーの電磁誘導の法則を用いた手回し発電機(ダイナモ)を発明したことで知られる。 - エジソン(Thomas Alva Edison)
トーマス・アルバ・エジソン(1847 ~ 1931年)は,アメリカの発明家で,電話機,無線機,白熱電球,映画,蓄音機,発電機など数多くの発明で知られる。
ページの先頭へ
【正弦波交流の特徴】
波形
正弦波交流(sinusoidal alternating current)の電流(又は電圧)は,時間と共に変化し,横軸に時間,縦軸に電流(又は電圧)の瞬時値( I )をとる直交座標で表したとき,その波形は,正弦波(サイン波ともいわれ) I = Im sin (ωt +ε) で表される。
ここで,Im は最大振幅(maximum amplitude ,電流の最大値,単に振幅ともいう),ωは角振動数(angular frequency ,角周波数),(ωt +ε) を位相(phase),εは t = 0 の時の位相で初期位相(initial phase)や初位相という。
なお,正弦波を除く交流(非正弦波交流)では位相を 0 とする位置(初期位相)は定められていない。
最大振幅と瞬時値
正弦波交流の電流(又は電圧)は,時間と共に変化する。電流は,回路の負荷とオームの法則に応じて変わるので,ここでは発電機の起電力について考える。
磁束密度 B ( テスラ T = Wb/m2) の一様な磁場において,それに垂直な面積 S (m2) の部分の磁束φ (Wb) は,
φ= B S
で与えられる。
ファラデーの電磁誘導の法則から,起電力 E は磁束 φ の変化速度に比例( E = ‐𝜕φ/ 𝜕 t )する。
ここで,磁束密度B (T) ,コイルの長さL (m) ,コイルの移動速度v (m/s) ,コイルの垂直面に対する角度をθとすると,磁束を垂直に横切る速度成分から,コイルに生じる起電力は,
E = ‐𝜕φ/ 𝜕 t = 2B L v sinθ= Em sinθ
で表される。
この式を瞬時式といい,ある時間の起電力 E を瞬時値(instantaneous value),瞬時値が最高(sinθ= 1 )の値を最大振幅(maximum amplitude),最大値(maximum value),波高値(peak value)などといい Em で表す。
周波数
角振動数ω,振動数(frequency ,周波数)ν,周期(period)T とは,
ω= 2πν= 2π T–1
の関係にある。
ちなみに,日本の発電所が作る交流の商用周波数(industrial frequency)は,ドイツ式の発電方式を導入した東日本で 50 Hz(ヨーロッパ,アフリカなど),米国式の発電方式を導入した西日本で 60 Hz(北アメリカ,南アメリカなど)と分かれている。
位相(phase)
位相とは,時間とともに周期的に変化する現象において全過程中の位置を示す量である。交流回路においては,電圧波形と電流波形のずれを指す。
位相のずれを位相差(phase difference)といい,2 つの波形を比較し,波形の位相が大きくなるときを位相の進み(進み位相),小さくなるときを位相の遅れ(遅れ位相),同じときを同位相(同相)という。
具体的に説明するため,下図には,電圧波形に対し電流波形の位相差を例示した。図では,横軸に時間をとっている。
図左端では,電圧波形に対し,電流波形が同じタイミングで変動,すなわち,ピークの位置が一致している。この場合を同位相という。
図中央では,電圧波形に対し,電流波形が左にずれている。このことは,横軸が時間なので,電圧がピークになる時間より早い時間に電流のピークを迎えていることを示す。
すなわち,電流が電圧より進んでいるので,電圧波形に対して電流波形が進み位相という。一方,電流波形に注目してみると,電圧波形が遅れていることになるので,電流波形に対して電圧波形は遅れ位相となる。
図右端は,図中央の電圧と電流を入れ替えた関係であるが,電圧と電流の何れを基準に考えるかで,進みと遅れの表現が逆転するので注意が必要である。
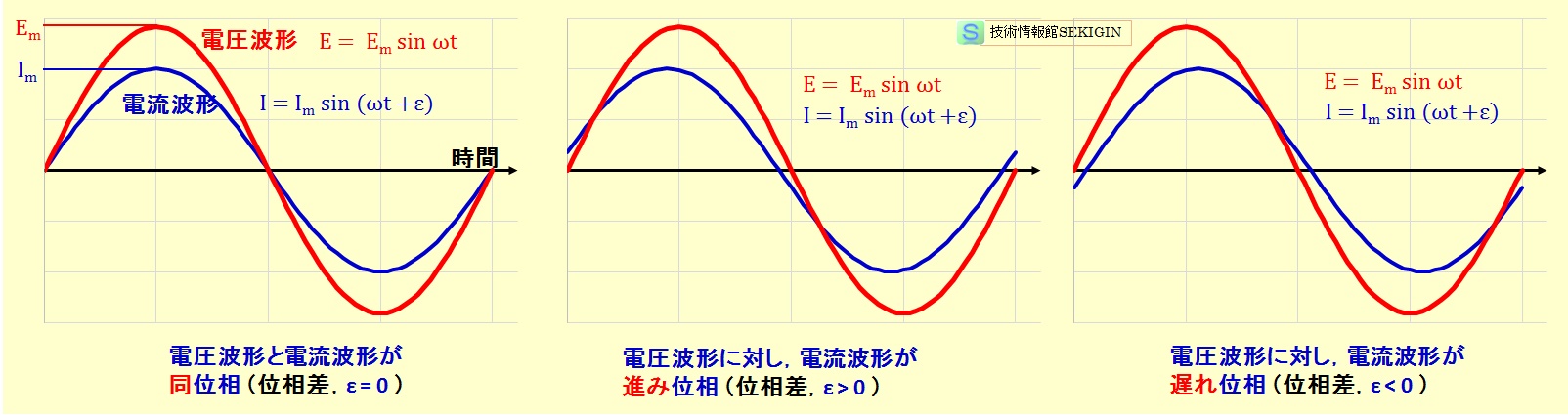
位相のずれ(位相差)
- ファラデーの電磁誘導の法則(Faraday's law of induction)
電磁誘導で,1 つの回路に生じる誘導起電力の大きさは,回路を貫く磁界の変化の割合に比例する。すなわち,ある閉回路を貫く磁束を Φ ( Wb :ウェーバ)としたとき,この回路に生じる誘導起電力 E( V :ボルト)は,磁束の変化の速度に比例( E = ‐𝜕φ/ 𝜕 t )する。 - ファラデー(Michael Faraday)
マイケル・ファラデー(1791年~1867年)は,イギリスの化学者,物理学者で,ファラデーの電磁誘導の法則,ファラデーの電気分解の法則,ファラデー定数など電磁気学,電気化学への貢献で知られる。 - 位相(phase)
時間とともに周期的に変化する現象において,周期中の位置を示す量をいう。通常は角度(度やラジアン)で表される。
例えば,正弦波で表される周期的な時間変化を y(t) = A sin(ωt + α) で表したとき,(ωt + α) を位相と言う。
なお,t = 0 の位相( α )は特に初期位相と呼ばれる。
ページの先頭へ
【コンデンサと交流(リアクタンス)】
交流とコンデンサ
回路に交流電流が流れる場合は,コンデンサ(キャパシタ)やコイル(インダクタ)では,直流とは異なる現象が起きる。
コンデンサ(capacitor)は,電気的に絶縁された導体に電圧を印加すると内部に電荷の偏り(静電誘導)が生じ,加えた電圧 V ,電荷の偏りを Q とすると,
Q = C V
になるまで電荷を蓄える。C は,導体の幾何学的な形状と導体の周囲の絶縁体により決まる比例係数で静電容量(electrostatic capacity),電気容量(electric capacity)やキャパシタンス(capacitance)とよばれる。
コンデンサに電源から直流電圧を加えると,下図左に示すように,静電誘導に伴い導線に瞬間的に電流が流れコンデンサを充電する。
誘電体は電流を通さないので,電極間の電位差が電源電圧と等しくなると電流は流れなくなる。その後に,電源から解放すると,逆の過程をへて電極間の電位差がなくなるまで放電する。
すなわち,コンデンサを含む回路では,充電,又は放電過程以外では電流が遮断される。
コンデンサ(キャパシタ)に交流電圧を加えると,下図中央に示すように,電極板は周期的に充電と放電を繰り返すとともに,電場の方向も反転する。
このため,誘電体内部の荷電(電子,イオン)の移動はないが,実質的には交流電流が流れているのと同等の現象になる。この磁束密度の時間変化に伴う電流は,一般的に見られる電荷の移動に伴う伝導電流(conduction current)に対し,変位電流(displacement current)という。
容量性リアクタンス
交流を通すのはコンデンサ(キャパシタ)の基本性質であるが,交流の通過し易さは,コンデンサの電圧電流比で表される容量性リアクタンス(condensive reactance ,記号 XC )で評価される。
容量性リアクタンス XC は,正弦波交流の周波数(ν),静電容量により決まる疑似的な抵抗で,電気抵抗と同じ次元を持つ(単位 Ω )。角周波数(ω),静電容量( C )との関係は,
![]()
で与えられる。
正弦波交流では,コンデンサ(キャパシタ)を流れる電圧( E )と電流( I )は時間と共に変化する。電流は電荷( Q )の時間変化で表され,
I (t) = d Q (t)/ dt ,Q (t) = C・E (t) ∴ I (t) = C・d E (t)/ dt
とできる。ここで,E (t) = Em・sin (ωt)とすると,
I (t) = C・Em・d sin (ωt)/ dt =ω・C・Em・cos (ωt)
∴ I (t) = ω・C・Em・sin (ωt +π/ 2 )
が得られる。すなわち,電流の位相は,電源電圧に対して π/ 2 ラジアン(rad),すなわち 90°進む。
容量性リアクタンスは,角周波数を限りなくゼロに近づけると(ω⇒ 0 ),無限大( XC ⇒∞)となる。すなわち,直流では開放状態になり,十分な充電時間経過後では電流がゼロになる。
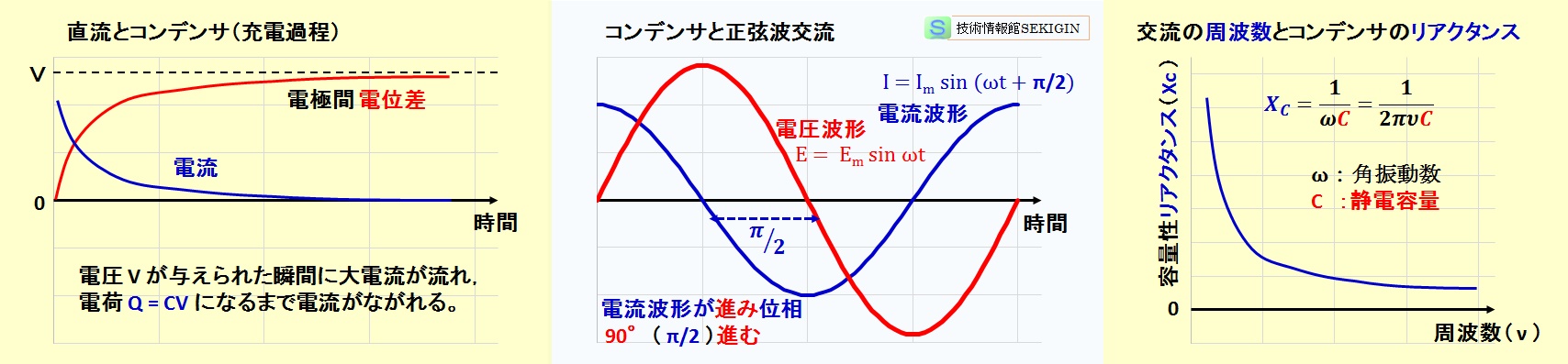
コンデンサの動作
- リアクタンス(reactance)
直流回路の電気抵抗(レジスタンス)に相当する交流回路のインピーダンスを複素数で表示した時の虚数部をいう。なお,実数部はレジスタンスや抵抗成分という。
リアクタンスには,インダクタンス(コイル)による誘導性リアクタンスとコンデンサによる容量性リアクタンスがある。 - コンデンサ(capacitor)
キャパシタ,蓄電器ともいわれ,静電容量により電荷を蓄えたり放出したりするための受動素子として用いられる。
コンデンサは,近接し相対する二つの電極(導体)の間に誘電体を挟み電気的に絶縁したものである。誘電体としては,空気,油,雲母,紙,プラスチックフィルム,磁器,酸化被膜等が用いられる。
用いる誘電体により,紙コンデンサ,オイルコンデンサ,真空コンデンサ,ガス封入コンデンサ,プラスチックフィルムコンデンサ,セラミックコンデンサ,電解コンデンサなどがある。他に電気二重層を利用した電気二重層コンデンサ,静電容量を加減できる可変コンデンサなどがある。
ページの先頭へ
【コイルと交流(リアクタンス)】
回路に交流電流が流れる場合は,コンデンサ(キャパシタ)やコイル(インダクタ)では,直流とは異なる現象が起きる。
一般的に,コイルといった場合は,流れる電流によって形成される磁場にエネルギーを蓄えることができるインダクタ(inductor)やインダクション・コイルといわれる受動素子を指すことが多い。
なお,電磁石,電磁弁,アクチュエータなどの磁場の発生を目的としたコイルはソレノイド(solenoid)と呼ばれる。
インダクタ(inductor)
コイル内の磁場の変化に比例して
ファラデーの電磁誘導の法則に従い誘導起電力(自己誘導;self-induction)が生じる。
また,誘導電流は,レンツの法則に従い磁場の変化を妨げる方向に流れるので,インダクタは交流電流を遅延させ再形成する能力があり,コンデンサなどを組み合わせることで,特定の周波数の信号だけを取り出す共振回路やフィルタ回路に用いられる。
インダクタは,高周波回路用,一般回路用,デカップリング回路用,電源回路用など多種多様の製品があり,構造,形状,用途などで分類が多数ある。
構造による基本的な分類には,円筒状のコイルの内部(コア)に用いる材料による分類がある。例えば,コアが空洞や非磁性体を用いた空心コイル,コアにフェライト( MnZn フェライトや NiZn フェライトなど)を用いたフェライトコアコイル,鉄・ケイ素・アルミニウムからなる合金センダストなどを用いた圧粉コアコイル,けい素鋼やアモルファス合金を用いた金属コアコイルなどがある。
インダクタの過渡応答
インダクタは,自己誘導作用により電流変化を妨げる方向に起電力(誘導起電力)を発生する。
下図左端に示すように,インダクタに電圧を加えても直ちに電流が流れず,ある時間を経過して電流値が一定になる。一方,電圧を取り去っても一定時間経過するまで電流がゼロにならない。この現象をコイルの過渡応答(過渡現象)という。
自己誘導作用によりコイルに発生する起電力( E )は,電流の変化率(⊿ I/⊿t )に比例する。
![]()
ここで,L はコイルの自己インダクタンスである。
従って,下図中央に示すように,電圧を加えた直後は徐々に電流が増大するので起電力は電源電圧以上に高くならないが,電圧を取り去った時は,電流の変化率が大きく,高い起電力が発生する。
誘導性リアクタンス
インダクタに時間的に変化する電流が通ると,自己誘導により,電流の変化を妨げる向き逆起電力が生じる。
インダクタ(コイル)の交流の通過し易さは,インダクタの電圧電流比で表される誘導性リアクタンス(inductive reactance ,記号 XL )で評価される。
誘導性リアクタンス XL は,交流の周波数(ν),自己インダクタンスにより決まる疑似的な抵抗で,電気抵抗と同じ次元を持つ(単位 Ω )。
角周波数(ω),自己インダクタンス( L )との関係は,
![]()
で与えられる。
正弦波交流では,コイル(インダクタ)を流れる電圧( E )と電流( I )は時間と共に変化するので,上述の自己誘導作用の式 E (t) = L・d I (t)/ dt と正弦波の電流を I (t) = Im・sin (ωt) で表すと,
E (t) = L・Im・d sin (ωt)/ dt =ω・L・Im・cos (ωt)
∴ E (t) = ω・L・Im・sin (ωt +π/ 2 )
が得られる。なお,E (t) = ω・L・Im・sin (ωt ) とした場合には,I (t) = Im・sin (ωt –π/ 2 ) となる。
すなわち,下図右端に示すように,電流の位相は,電源電圧に対して π/ 2 ラジアン(rad),すなわち 90°遅れる。
誘導性リアクタンスは,角周波数と共に大きくなるが,限りなくゼロに近づけると(ω⇒ 0 ),誘導性リアクタンスが限りなくゼロ(XL ⇒ 0 )になる。すなわち,直流では短絡状態となり,インダクタに用いた導体の抵抗( R )に依存した電流が流れる。
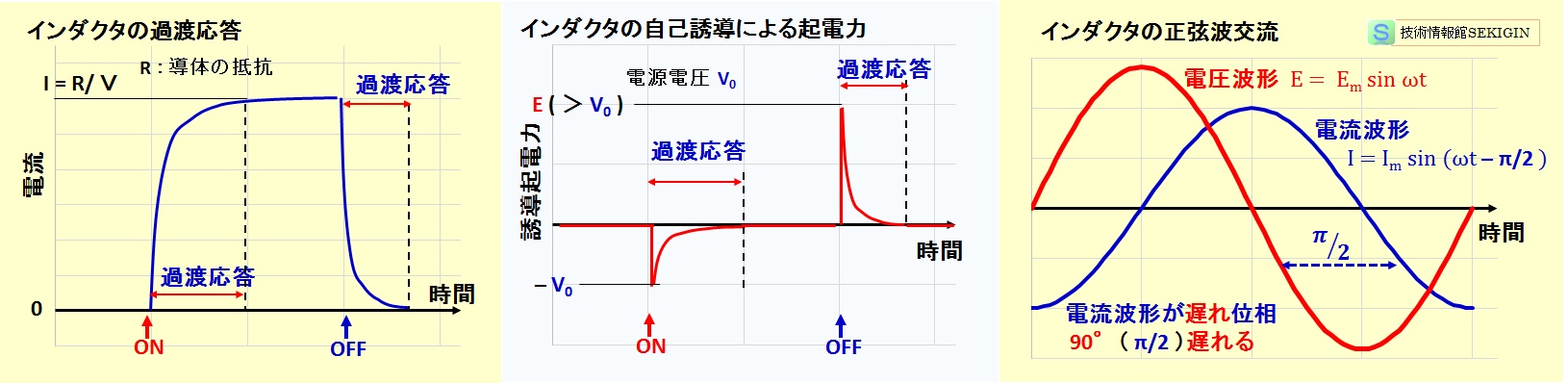
インダクタ(コイル)の動作
【参考:基礎用語】
- ソレノイド(solenoid)
コイルの一種で,円筒形に絶縁された導体を螺旋状に長く巻いたもので,電流を流して磁場の発生を目的としたもの(電磁石),それを利用した装置(電磁弁,アクチュエータなど)を指す。
一般的に,コイルといった場合は,流れる電流によって形成される磁場にエネルギーを蓄えることができるインダクタやインダクション・コイルといわれる受動素子を指すことが多い。 - インダクタ(inductor)
俗にいうコイルで,コイル内の磁場の変化に比例してファラデーの電磁誘導の法則に従い誘導起電力(自己誘導;self-induction)が生じる。
また,誘導電流は,レンツの法則に従い磁場の変化を妨げる方向に流れるので,インダクタは交流電流を遅延させ再形成する能力があり,コンデンサなどを組み合わせることで,特定の周波数の信号だけを取り出す共振回路やフィルタ回路に用いられる。
インダクタには,高周波回路用,一般回路用,デカップリング回路用,電源回路用など多種多様の製品があり,構造,形状,用途などで分類が多数ある。 - 相互誘導(mutual induction)
二つのコイル( A , B )が磁気的に結合しているとき,2つのコイルに流れる電流が互いに影響を及ぼす現象をいう。例えば,回路 A を流れる電流が変化(時間 Δt の間に ΔI 変化)したとき,電磁誘導により,回路 B に誘導起電力(-M(ΔI/Δt) )が生じる現象である。この時,比例定数 M を相互インダクタンス(mutual inductance)という。 - 自己誘導(self-induction)
閉ループ回路の電流が時間的に変化すると,電流の変化を妨げる向きに回路に逆起電力が生じる現象。 - インダクタンス(inductance)
コイルを流れる電流を変化させたとき電磁誘導によりそのコイル,あるいは他のコイルに発生する起電力の大きさを表わす量をいい,単位には,アメリカの物理学者ヘンリーに因んでヘンリー( H )が用いられる。 - 自己インダクタンス(self-inductance)
自己誘導係数ともいい,自己誘導で生じる起電力の大きさを表わす量(単位 ヘンリー H )で,コイルの巻数,寸法,周囲の媒質によって定まる定数である。
ページの先頭へ
【インピーダンスとは】
交流回路に交流電流が流れる場合は,直流回路と異なり,コンデンサ(キャパシタ)やコイル(インダクタ)が電流の流れを妨げるとともに,電圧波形に対する電流波形の位相にも影響する。
正弦波交流の場合,抵抗( R )は電圧波形と同相であるが,前述したようにインダクタ(コイル)では電圧波形に対し,電流波形はπ/ 2(rad)遅れ,キャパシタ(コンデンサ)では,π/ 2(rad)進む。
従って,交流回路中に抵抗,インダクタ,キャパシタが混在する場合の電流の流れにくさを表す量は,位相を考慮したものが必要になる。
これをインピーダンス(impedance)といい,直流回路の電気抵抗(レジスタンス)に相当し,記号 Z ,単位Ωオームを用いるが,一般には複素量で表される。複素数のインピーダンスにおいて,実数部をレジスタンスや抵抗成分,虚数部をリアクタンスという。
なお,インピーダンスの逆数はアドミッタンス(admittance)といい,直流回路の電気伝導度(コンダクタンス)に相当し,記号 S ,単位 S ジーメンスを用いる。
インピーダンスの定義
電気回路のインピーダンスは,前述のリアクタンスの説明ど同様に電圧と電流の比で表され,疑似的な抵抗で,電気抵抗と同じ次元を持つ(単位 Ω )。
インピーダンスの表示は,複素数で表示するフェーザ表示(phasor)を用いて表すのが一般的である。なお,フェーザ表示とは,電気工学や波動光学などにおいて正弦信号を複素数で表現する表示方法である。
抵抗(XR ),容量性リアクタンス(XC ),誘導性リアクタンス(XL )は,虚数単位 j を用いたフェーザ表示では,
![]()
で与えられる。なお,虚数 j × j = –1 である。
抵抗,インダクタ,キャパシタが混在する場のインピーダンスの求め方については,交流回路の計算例で紹介する。
電気抵抗(electric power)
文脈から電気抵抗であることが明らかな場合は,単に抵抗やレジスタンスともいう。抵抗は,電流の流れ難さを表す。電気抵抗の国際単位系 (SI) における単位はオーム(記号:Ω)である。
電気抵抗の逆数は電気伝導度,コンダクタンスと呼ばれ,電流の流れやすさを表す。
ページの先頭へ
【交流電力とは】
電力(electric power)とは, 単位時間( 1 秒)当たりの仕事率(power)に対して,電気工学で用いる術語で,国際単位系(SI)で,1 秒当たり 1 ジュール( J )の仕事率(ジュール毎秒(J/ s)を 1 ワット( W )と定義されている。なお,電力を時間ごとに積算した量を電力量(electric energy)と呼び,電力とは区別される。
直流回路の電力
電力( P ;ワット)は,電流( I ;アンペア)と電圧( V ;ボルト)の積 P = I × V で求められる。なお,回路の抵抗( R ;オーム)のとき,オームの法則を適用し,P = I・V = I2・R = V2・R−1 で求められる。
電力の単位について
ワット( W )は,組立単位で,SI 基本単位で表すと,
1 W = 1 J・s−1 = 1 m2・kg・s−3
となる。
電流の単位アンペア( A )はSI 基本単位で,電位差の単位ボルト( V )は組み立て単位( 1 V = 1 m2・kg・s−3・A−1)である。
従って,電流と電圧の積の単位は,
P = I × V = A × V = A × m2・kg・s−3・A−1 = m2・kg・s−3 = J・s−1 = W
となる。
交流回路の電力
電圧・電流とも時間と共に変化するので,電力も時間と共に変化する。このため,交流の電力は,各瞬間での電圧と電流の積の時間平均として求められる。
なお,回路に抵抗成分,リアクタンス成分(コイルやコンデンサー)を含む場合は,エネルギーを消費するのは抵抗成分(有効電力)だけで,リアクタンス成分(無効電力)はエネルギーを消費しない。従って,直流回路と異なり,回路の両端の電圧と回路に流れる電流の積は,見かけの電力(皮相電力)となる。
このように,交流回路の電力は,有効電力,無効電力,皮相電力の 3 種に分けられる。
有効電力(effective power)とは,負荷回路のインピーダンスのうち抵抗成分が消費する電力で,消費電力ともい,記号 P ,単位ワット W が用いられる。
ここで,周期 T とし,ある時点での瞬時電力 p(t) (instantaneous electric power)を 1 周期( T )に渡って平均した値は,有効電力 P と呼ばれ,
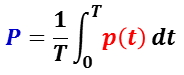
で定義される。
無効電力(reactive power)とは,負荷回路のインピーダンスのうちリアクタンス分にかかる電力で,記号 Q 又は Pq ,単位バール var が用いられる。無効電力は,電圧の調整のために電源と負荷を行ったり来たりするだけで,負荷で消費されない電力である。
皮相電力(apparent power)とは,電源から送り出される電力で見かけの電力とも呼ばれ,記号 S 又は Ps ,単位ボルトアンペア V A が用いられる。皮相電力は,瞬時値電流の絶対値と瞬時値電圧の絶対値の積を 1 周期にわたって積分したもので,有効電力と無効電力をベクトル合成したものである。
有効電力,無効電力,皮相電力の関係
![]()
ページの先頭へ
【正弦波交流の電力】
交流には,正弦波,矩形波,三角波,のこぎり歯状波,パスル波などがある。次には,商用電源として最も身近な正弦波交流の電力を紹介する。
有効電力(reactive power)
電圧の最大振幅 Vm ,電流の最大振幅 Im の正弦波交流において,ある時刻での瞬時電圧 v(t) ,瞬時電流 i(t) を,
v(t) = Vm sin(ωt) ,i(t) = Im sin(ωt – φ)
と表わされる。ここで,角振動数 ω = 2π T–1 ,位相差 φとする。
従って,有効電力 P は,
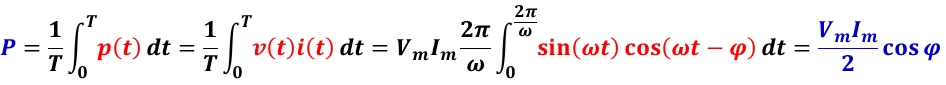
となる。位相差φを力率角,その余弦 cos φ を力率(power factor)という。
電力の実効値 V ,電流の実効値 I とおくと,
![]()
とできる。
無効電力(reactive power)
負荷で消費されない電力で,自己インダクタンスに由来する誘導負荷,静電容量に由来する容量負荷から生じる。
誘導負荷による無効電力は遅れ無効電力,容量負荷による無効電力は進み無効電力と呼ばれる。
電圧の調整に使われるものとして,電圧(V)と電流(A)の実効値の積(V・A)に力率角φの正弦(sin φ)をかけたものをいい,記号 Q ,単位バール(var)で表される。
![]()
力率が小さいほど無効電力は大きくなり無駄な電流を流していることを意味する。なお,正弦 sin φを無効率という。
皮相電力(apparent power)
上述の電圧(V)と電流(A)の実効値の積(V・A)は,単純に交流の瞬時値電流の絶対値と瞬時値電圧の絶対値の積を 1 周期にわたって積分したものである。これを皮相電力といい,記号 S 又は Ps ,単位ボルトアンペア(V A)で表される。
![]()
三相交流回路の場合,三相電力 P は,各相における電力の総和として表される。相電圧 Ep ,相電流 Ip ,力率 cos φのとき,次式が成り立つ。
![]()
ページの先頭へ