物理 第三部:流体の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,ベルヌーイの定理に関連し, 【ベルヌーイの定理とは】, 【エネルギー保存とベルヌーイの式】, 【ベンチュリ管,ピトー管】, 【水頭とは(エネルギー保存)】 に項目を分けて紹介する。
【ベルヌーイの定理とは】
前節の流体の運動で紹介したように,ベルヌーイの定理(Bernoulli's theorem)により流体の挙動を平易に表すことができ,力学的エネルギー保存の法則に相当する定理である。
ベルヌーイの式は,外力が保存力であること,密度が圧力のみの関数となるバルトロピー流体であることに加えて,適用する完全流体の分類に応じて,定常流の条件で成り立つものと,渦なしの流れの条件で成り立つものに分けられる。
定常流におけるベルヌーイの定理
外力が保存力で,非粘性のバルトロピー流体の定常な流れで,速度ベクトルν,圧力 p ,密度ρ,外力 f のポテンシャルΩ( f =-∇Ω)としたとき,
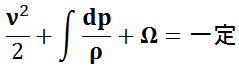
が流線上のみで成り立つ。
一様な重力場で,重力加速度の大きさ g ,鉛直方向の座標 z とすると,
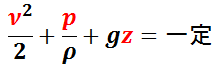
と書ける。
【参考:基礎用語】
- ベルヌーイ(Daniel Bernoulli)
ダニエル・ベルヌーイ(1700年~1782年)は,スイスの数学者・物理学者。1738年に『流体力学』を出版。ベルヌーイの定理「空気や水の流れがはやくなると,そのはやくなった部分は圧力が低くなる。はやく流れるほど圧力は下がる。」など,流体力学の基礎を築いた。 - 完全流体(perfect fluid)
理想流体(ideal fluid),非粘性流体(inviscid fluid)ともいわれ,理想化して粘性を無視した取扱いをする仮想的な流体で,ベルヌーイの定理が成り立つ。
粘性が存在しないことは,流体が運動してもせん断応力(接線応力)が作用しないことと同義で,いわば力学での摩擦力の無視と同等に考えられる。 - 定常流(steady flow)
流管の中のある点を採った時,その点での流速が時間と共に変化しない流れをいう。 - バルトロピー流体
多くの流体では,密度が一定(ρ=一定)であったり,圧力が密度に依存( p(ρ) )したりする。圧力が密度に依存することを順圧(barotropic)やバルトロピックといい,この性質の流体をバルトロピー流体という。
従って,バルトロピー流体では,最終的な未知変数は速度(μ,ν,ω)と圧力 p の 4 つになる。
ページの先頭へ
【エネルギー保存とベルヌーイの式】
下図のように,密度ρの非圧縮性完全流体の流れに流管をとり,任意の 2 点( A ,B )を考える。
各点の高さを ZA ,ZB とし,流速を vA ,vB ,断面積を dSA ,dSB ,断面に鉛直方向の圧力を pA ,pB とする。
時刻 t で A ,B 内にあった流体が,時刻 t + dt に A’,B’に移動した時の仕事( dW )とエネルギー変化量( dE )を考える。
仕事( dW )
仕事は,物体に作用する力と力の方向への移動距離の積で得られる。
圧力は流管の側面からも作用するが,流体の運動に垂直な力は仕事をしないので, A ,B の断面に対し鉛直方向に作用する圧力を用いて,流体に作用する力は,
断面 A:pA dSA
断面 B:- pB dSB
となる。
dt 時間後の流体の移動距離は,
断面 A:vA dt
断面 B:vB dt
となるので,仕事 dW は,
dW =pA dSA・vA dt-pB dSB・vB dt
となる。
エネルギー変化量( dE )
A ,B 内の流体が,dt 時間後に,A’,B’に移動している。従って,この間のエネルギー変化量 dE は,
dE =( A’,B’間のエネルギー)-( A ,B 間のエネルギー)
で与えられるが,A’と B の間の変化はないと仮定できるので,
dE =( B ,B’間のエネルギー)-( A ,A’間のエネルギー)
とできる。
従って,B ,B’間の流体の質量(ρdSB・vB dt ),重力加速度 g ,高さ ZB とから
位置エネルギー( UB ):ρdSB・vB dt・g ZB
運動エネルギー( KB ):ρdSB・vB dt・1/2 vB2
とできる。
A ,A’間のエネルギーも同様にして与えられるので,エネルギー差 dE は,
dE =( UB+KB )-( UA+KA )
となる。
エネルギー差は,成した仕事と一致( dW=dE )する。また,非圧縮性流体であるため,移動した流体の体積は,dSB・vB dt = dSA・vA dt とできる。
従って,以上をまとめると,
![]()
となり,両辺を密度で割ることで,一つの流管に関するベルヌーイの式
![]()
が得られる。

完全流体の運動とエネルギー
- 仕事(work)
物理学においては,力 F を受けた物体が,力の方向に x 移動(変位)した時に,ベクトルの力と変位の積(内積)を,その力のした仕事 W(=Fx )という。
エネルギーは,“物体や系が持つ仕事をする能力”と定義され,仕事の前後のエネルギー差( dE )が仕事 W に相当する。 - 運動エネルギー(kinetic energy)
運動エネルギー( K )は,質量 m の物体の運動に伴うエネルギーで,物体の速度 v を変化させる際に必要な仕事で,K = 1/2 mv2 で表される。 - 位置エネルギー(potential energy)
位置エネルギー( U )は,物体が「ある位置」にあることで物体が持つ(蓄えられた)エネルギーで,重力場(重力加速度 g )で質量 m の物体が高さ( h )にあるときの位置エネルギーは,U= mgh で表される。 - 非圧縮性流体(incompressible fluid)
一般に圧力によって流体の密度が変化するので圧縮性流体(compressible fluid)と呼ばれるが,流体の速度(圧力変化)が小さく,密度の変化が無視できる場合には非圧縮性流体として扱われる。 - エネルギー保存の法則(law of the conservation of energy)
“閉じた系(外界とエネルギーの出入りが無い系)において,エネルギーの移動,形態の変更などによっても,その総量が変化しない”と定義され,物理学における保存則(conservation law)の一つで,短縮してエネルギー保存則ともいわれる。
19 世紀までに力学的エネルギー保存の法則(principle of mechanical energy)が確立され,その後に熱現象も含めた熱力学の第一法則(孤立系のエネルギーの総量は変化しない)がマイヤー,ジュール,ヘルムホルツらにより確立されたことで,音,光,電磁気,化学変化,原子核反応等を含めた自然現象を支配する基礎法則となった。
ページの先頭へ
【ベンチュリ管,ピトー管】
ベンチュリ管(Venturi tube)
イタリアの物理学者ジョヴァンニ・バッティスタ・ヴェントゥーリが発明したもので,流体の流れを絞ることで流速を増加させ,低速部にくらべて低い圧力を発生するベンチュリ効果(Venturi effect)を応用した管で,流量計,霧吹き,キャブレター,エアブラシなどに利用されている。
太い部分の断面を A ,細い部分の断面を B とした時,非圧縮性流体の場合,各断面を単位時間に通過する流体の量(流速×断面積)は同一であり,
vASA = vBSB = Q (連続の方程式という)
となり,断面積の小さい方の流速が増加することが分かる。
一方ベルヌーイの式から,
![]()
とでき,断面 A と B が水平の位置,すなわち高低差がない場合は ZA = ZB となるので,連続の方程式とから圧力差を求めると,
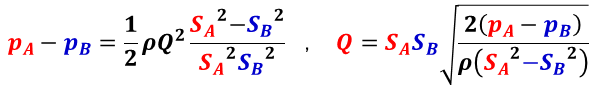
となり,断面積の小さい方,流速の大きい方の圧力が低くなる,また,断面積の異なる箇所の圧力差を求めることで,流量 Q を求めることができる。
ピトー管(pitot tube)
フランスの物理学者アンリ・ピトーが発明した流体の流れの速さを測定する計測器で,航空機の速度計や風洞などに使用されている。
ピトー管は,二重になった管を基本構造とし,内側の管は先端部分 A に,外側の管は側面 B に穴が空き,二つの管の奥の圧力計で圧力差(動圧という)を測定することで流速が求められる。
流速 v の流体中にピトー管の先端を流速に向き合うように配した場合には,先端部分 A では流れが妨げられるので流速 vA = 0 となる。一方,側面の穴 B の周辺は,粘性の低い流体では側面の影響をほとんど受けず,vB ⋍ v とできる。
ベルヌーイの式において,流体の密度ρ,先端の穴と側面の穴の高低差が無視できる( zA = zB)場合には,動圧(圧力差)と流速は,
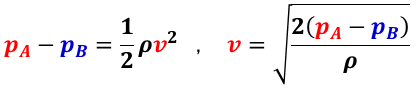
で与えられる。
実際には,穴の部分が流速に影響するため,精確な速度の算出では,個々のピトー管において,実験的に求められた補正係数が必要になる。
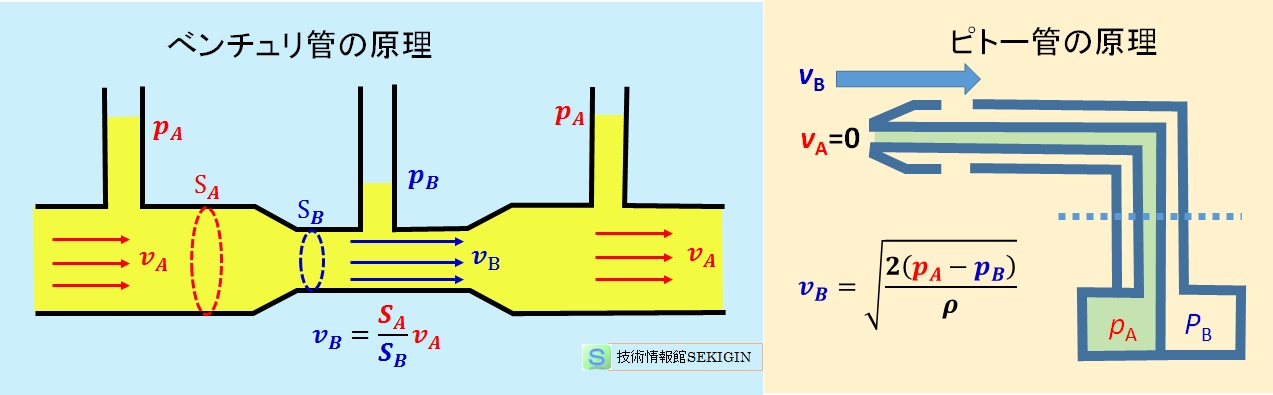
ベンチュリ管,ピトー管
【参考:基礎用語】
- ベンチュリ効果(Venturi effect)
流体の流路において,部分的に断面積を狭めたとき,流体の流速が増加し,圧力の低い部分が作り出される現象をいう。流量を一定にした場合のベルヌーイの定理から導かれる。 - 動圧(dynamic pressure)
ベルヌーイの定理における流体の運動エネルギーを表わす項 1/2 ρv2 をいう。
ページの先頭へ
【水頭とは(エネルギー保存)】
エネルギー保存の法則(law of the conservation of energy),すなわち物理的・化学的変化において,これに関与する各種のエネルギーの総和が,変化の前後で変らないという法則が成立する。
流体の場合は,単位重量当りの運動エネルギー,位置エネルギーを長さの次元を持つ流体の高さ(高度差)で表すことがある。これは水頭(hydraulic head)又はヘッド(head)といわれる。
水頭には,運動エネルギーに相当する速度水頭(velocity head),位置エネルギーに相当する位置(高度)水頭(elevation head),圧力水頭(pressure head)がある。この他に,流路の影響(管の摩擦,曲がりなど)で失われるエネルギーを損失水頭(loss of head , head loss)という。これらの総和を全水頭(total head)という。
エネルギー保存の法則と同様に,一様重力のもとでの完全流体(非粘性・非圧縮流体)の定常な流れに対して全水頭は一定である。
圧力 p ,密度ρ,重力加速度 g ,流速 v ,高低差 h とした時,
![]()
この式は,ベルヌーイの式の両辺を重力加速度 g で除した式と同等である。
ページの先頭へ